§ 2.5. Скалярний добуток векторів. Кут між векторами.

Вектори і можна перемножити двома способами. В одному випадку результатом буде число (скаляр), а у іншому – вектор. Відповідно визначаються скалярний і векторний добуток двох векторів.

Скалярним добутком двох ненульових векторів і називається число, яке дорівнює добутку довжин цих векторів на косинус кута між ними. Позначається скалярний добуток одним із символів , , . Таким чином:

(5.1)

де – кут між векторами і .

Скалярний добуток можна задати, також, за допомогою проекцій одного вектора на інший:

(5.2)

Якщо, принаймні, один із двох даних векторів нульовий, то скалярний добуток вважається рівним нулю.

Приклад 1. Відомо, що і кут між векторами і дорівнює . Знайти скалярний добуток .

Розв’язання. Використовуючи формулу (5.1), маємо:

.

Властивості скалярного добутку:

1. 

2. 

3. 

4. 

Нехай вектори і задані своїми координатами:

Використовуючи властивості скалярного добутку, дістанемо

. (5.3)

Формула (5.3) визначає скалярний добуток у координатній формі. Як бачимо, скалярний добуток двох векторів дорівнює сумі добутків відповідних координат.

Приклад 2. Знайти скалярний добуток векторів і

Розв’язання.

З рівності (5.1) безпосередньо випливає формула для обчислення кута між двома ненульовими векторами:

(5.4)

або

(5.5)

З останніх формул отримаємо умову ортогональності (перпендикулярності) двох ненульових векторів:

(5.6)

або

. (5.7)

Приклад 3. Точки А (-3;0;1), В (2;4;-5), С (0;2;3) є вершинами трикутника. Знайти трикутника АВС.

Розв’язання. Визначимо спочатку координати потрібних нам векторів:

,

Застосовуючи формулу (5.5), дістанемо

§ 2.6. Векторний добуток векторів.

У порядкована трійка ненульових векторів називається правою, якщо після зведення її до спільного початку для спостерігача, що знаходиться на кінці вектора , поворот на найменший кут від вектора до вектора здійснюється проти руху годинникової стрілки Векторним добутком двох неколінеарних векторів і називається вектор , який визначається наступними трьома правилами:

1. довжина вектора задається формулою

, (6.1)

де – кут між векторами і ;

2. вектор перпендикулярний до кожного з векторів і ;

3. вектори утворюють праву трійку векторів (рис.8).

Перше правило визначає довжину вектора , а два останні –його напрям. Легко бачити, що добуток правої частини формули (6.1) дорівнює площі паралелограма, побудованого на векторах і . Отже, довжина вектора дорівнює площі вказаного паралелограма.

Вважається, що векторний добуток двох колінеарних векторів дорівнює нульовому вектору.

Векторний добуток векторів і будемо позначати або .

Властивості векторного добутку:

1. ;

2. ;

3. ;

4. якщо векторний добуток двох ненульових векторів і дорівнює нульовому вектору, то вектори і колінеарні.

Нехай вектори і задані своїми координатами:

Тоді:

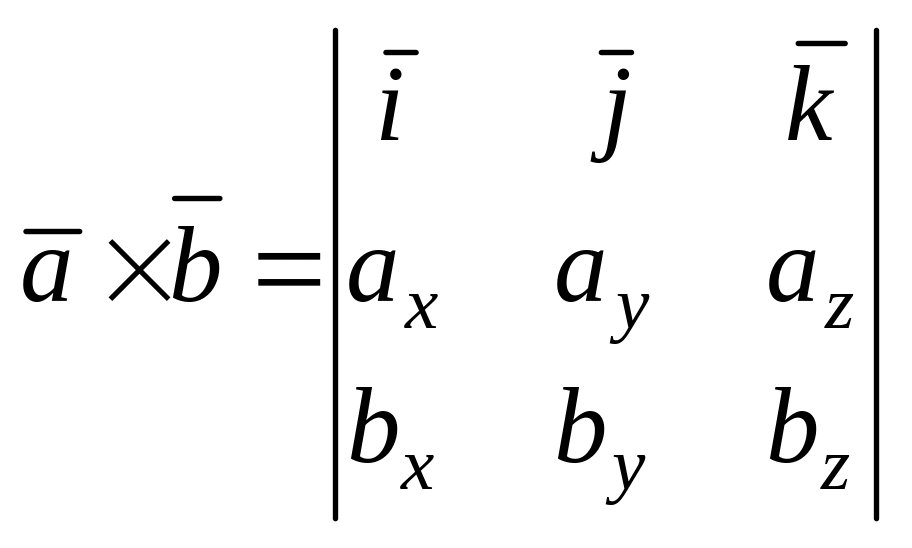, (6.2)

або

. (6.3)

Площа паралелограма й площа трикутника, побудованих на векторах і , обчислюються наступним чином:

. (6.4)

Приклад 1. Задані два вектори і . Знайти: а) вектор, перпендикулярний до кожного з векторів і ; б) площу трикутника, побудованого на векторах і .

Розв’язання. а) Відмітимо, що задача не має єдиного розв’язку, тобто існує нескінченне число колінеарних векторів, які задовольняють умовам цієї задачі. Одним із таких векторів є векторний добуток (див. означення):

.

б) Використовуючи (6.4), отримаємо

(кв. од.).