

|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 - 24 |
|
vout @ vω |
|
|
|
|
|
|
|
|
|
|
|
|
CHUNG-YU WU |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d |
v = - |
I o -iω |
= |
dvω |
= - |
iω |
Þ i = |
|
IoCω |
|
|||||
|
|
dt |
C |
( C |
|
||||||||||
dt out |
|
C |
C |
|
ω |
C |
+C ) |
||||||||
|
|
|
|
|
|
|
ω |
|
|
ω |
|||||
dvout |
= - |
|
Io |
|
slew degradation |
|
|
|
|
||||||
|
CC +Cω |
|
|
|
|
||||||||||
dt |
|
|
|
|
|
|
|
|
|||||||
§ 6-4.2 Single-stage OP AMPs
SR = Io
CL
Different phase margins
Þ different settling behavior.
- |
Vo |
|
+ |
||
CL |
||
Vi |
||
|
Io First-stage bias current
SR of the folded cascode OP AMPs
|
|
|
|
|
|
+ VDD |
|
|
|
|
|
|
|
I |
p |
M5 |
M6 |
|
VBIAS1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Io |
|
|
|
|
VX |
Ip |
|
|
|
|
|
|
|
|
VY |
|
|
|
|||
|
|
|
|
|
Ip-Io |
|
|
|
||
|
|
V |
|
|
|
Ip |
|
|
||
|
off |
BIAS2 |
|
M3 |
M4 |
|
|
|||
|
|
|
|
Io |
|
|
||||
|
|
|
|
|
V |
out |
||||
|
|
|
|
|
|
|
||||
M1 |
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V |
|
|
|
|
|
I |
|
-I |
CL |
|
|
|
|
|
|
|
p |
|
|||
|
Vs |
|
|
|
|
|
o |
|
|
|
|
|
|
|
M7 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
8 |
|
|
|
|
Io |
|
|
|
|
|
VB |
|
|
|
|
|
|
|
|
|
M9 |
M10 |
|
|
||
|
|
|
|
|
|
- VSS |
|
|
|
|
SR = Io
CL
* If Ip=Io, we can keep M5, M1 and Io current source in saturation.

6 - 25
CHUNG-YU WU
The change of Vx is not significant because the gain of the
common-source amplifier M1 is nearly equal to –1. When M2 is
turned on, the recovery time of Vx is very short.
*If Ip < Io, the current source Io is forced to linear region and Vs ↓
Vx ↓ . The decrease of Vx is large. Thus the recovery time of Vx
when M2 is turned on is very long, Þ The settling is slow down. How to solve this problem?
(1)Keep Ip = Io as the optimal design.
(2)Add clamping devices between VDD and Vx(VY)
+VDD
VBIAS1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VBIAS1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
M11 |
M12 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 
In normal operation, M11 and M12 are turned off by setting
VDD-Vx < VTH11,VTH12.
§6-5 Power supply rejection ratio (PSRR)
§6-5.1 Low frequency analysis for integrators
+ VDD
M3 




 M4
M4
Cgd |
|
Vin |
M2 |
M1 |
|
Cgs |
|
|
Io |
|
- VSS |
|
CI |
|
CC |
gain |
Vout |
stage |
|
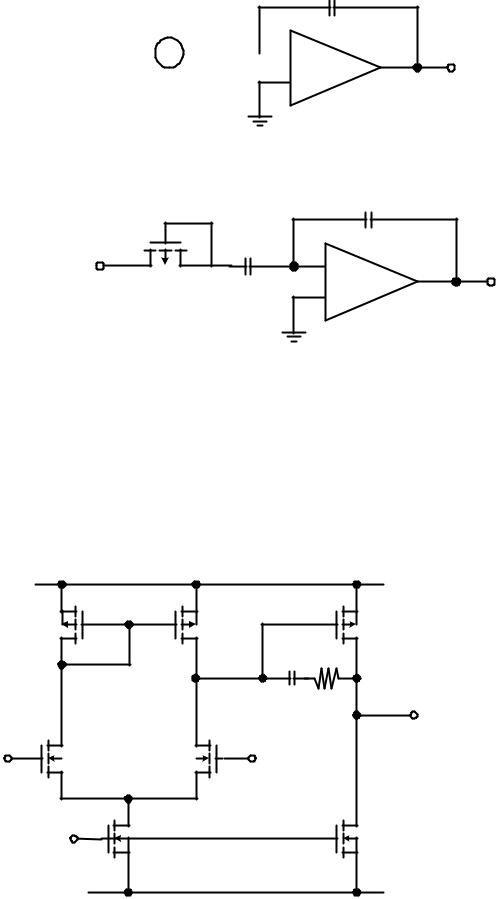
6 - 26
¶V |
|
Cg s é ¶I |
|
1 |
|
¶V |
|
ù Cg d |
|
1 ¶I |
|
CHUNG-YU WU |
||||||||||
|
o |
|
|
|
o |
|
||||||||||||||||
out |
@ |
|
|
ê |
|
|
|
|
+ |
GS 1 |
ú + |
|
|
|
|
|
|
|
||||
¶V |
C |
I |
¶V |
|
|
2g |
m1 |
¶V |
S S |
C |
I |
|
2g |
m3 |
|
¶V |
S S |
|||||
S S |
|
|
ë |
S S |
|
|
|
|
û |
|
|
|
|
|
||||||||
Io |
C |
|
I |
-VSS


 -
-
Cgs +
¶V |
Cg d é |
|
¶I |
o |
1 |
ù |
|
Cg s |
|
1 ¶I |
o |
|||||
out |
@ - |
|
1 |
- |
|
|
|
ú |
+ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
¶VDD |
ê |
|
¶VDD |
|
|
|
CI 2gm1 ¶VDD |
|||||||||
CI ë |
|
|
2gm3 û |
|
||||||||||||
CI
VDD |
M3 |
Cgd |
- |
|
+ |
||
|
|
Ref. : IEEE , JSSC , vol.SC-15 , pp.929-938 , Dec. 1980.
*Cgs / CI and Cgd / CI have a strong effect on PSRR+ and PSRR-.
*Small CI Þ chip area↓ but PSRR↓.
§6-5.2 High frequency analysis for OP AMP’s
Ref. : IEEE JSSC , vol. sc-19 , pp. 919-925 , Dec. 1984.
+VDD
M3 |
M4 |
M6 |
|
|
|
CC |
|
|
V1 |
V |
|
|
|
Rz |
o |
|
|
|
|
Vi + |
M2 |
Vi - |
|
M1 |
|
|
M5 |
M7 |
VBIAS |
|
|
- VSS |

6 - 27
CHUNG-YU WU
|
|
¶V |
|
¶Vo |
|
|
|
|
|
|
o |
|
¶Vi V =0 |
é |
|
|
ù−1 |
* |
PSRR+ º |
¶V |
= |
¶V |
||||
i |
o |
= ê |
|
io |
ú |
|||
|
|
¶V |
|
¶V |
ê¶V |
DD Vo =0 |
ú |
|
|
|
o |
|
o |
ë |
|
û |
|
|
|
¶VDD |
|
¶VDD Vo =0 |
|
|
|
|
|
How to calculate |
|
¶Vio |
|
|
|
|
|
|
|
|
¶VDD |
|
|
|
|
|
|
|
|
|
VDD |
|
|
|
|
|
|
|
|
~ |
Vi |
|
|
|
|
|
Vio |
- |
|
|
|
|
|
|
|
|
|
+ |
|
|
Vio |
|
|
VSS |
|
V1 |
CC Rz=1/gm2 |
Vio |
Go1 |
gm2(V1-Vi ) |
Go2 |
|
|
|
gm1Vio |
C1 |
|
~ Vi( from VDD )
PSRR+ (s) @ s +Go 1Go 2 /( gm2 Cc ) s + gm1 / Cc
where Go1=go4 ( go2 is connected to the drain of M5 which is open-circuited, i.e. rds5 ® ¥)
(rds7 ® ¥)
Go1Go2/(gm2Cc) < gm1/Cc
Þ Low-frequency LHP zero degrades the PSRR .
6 - 28
CHUNG-YU WU
*To improve PSRR, Cc must be decoupled from the gate of M6 to eliminate the LHP zero .

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
" |
|
# |
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
" #$ |
|
||||
% & |
' () |
|
|
|
* |
|
||||
|
|
|
+,- |
|
|
|
., |
|
||
/ 00 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
/ -' |
|
2 3-, |
|
|
*' 3-, |
|
|
|||
|
|
45 6 |
|
|
4! 6 |
|
|
|||
, |
|
* ', |
|
|
|
&*, |
|
|
|
|
!
* / 7
89 * ' 3 :

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
89 ; ' () |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
< < = |
|
;2ω 2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= ω |
|
|
! " |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
89 > |
= |
= |
ω |
= |
× π |
× × × − |
||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||
+ : 7 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
89 > = |
|
≥ |
|
µ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
= |
|
|
|
|
|
= |
|
|
|
||||||||||||||||||
? & 7 @ |
||||||||||||||||||||||||||||
? : |
||||||||||||||||||||||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
= |
|
|
µ |
= |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= |
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||
. % |
||||||||||||||||||||||||||||
8?A |
||||||||||||||||||||||||||||
89 > |
|
( ) |
|
|
= |
( ) |
|
|
= |
|
|
= |
|
|
|
|
||||||||||||
|
( ) |
|
( ) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= = |
|
= |
|
( ) |
|
|
|
||||||||||||||||||||
|
|
|
( ) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= |
|
|
|
= |
|
|
|
|
µ |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# / |
|
|
|
|
||||||||||||||||
89 > = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
+ |
+ |
|
λ |
λ |
|
|
||||||||||||
> |
|
λ |
= |
− |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
|
|
≈ |
|
|
|
|
≈ |
|
≈ |
|
||||||||
|
|
(λ |
)( |
λ ) |
||||||||||||||||
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
≈ |
|
|
ω |
|
≈ |
|
ω |
|
≈ |
|
|||||||||
λ |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
||||||
B :
ω: : 7 C
7
89 > B → |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
+ |
+ |
|
≈ |
|
|
|
≈ Ω |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
B → |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
|
|
= |
Ω |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
µ |
|
|
[ ( |
+ |
|
− |
|
|
|
)] |
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1
A 7
/ A 7

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≈ |
|
|
|
|
|
|
|
|
|
||||||||||
89 > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
≈ |
|
|
||||||||||||
|
|
|
|
|
|
|
( − ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ≈ |
6 |
|||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≈ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
( |
− ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
/ ! !: ! |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
D " |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
89 > |
|
|
|
|
≈ |
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
( ) = |
( ) |
≈ |
|
|
|
|
|
|
≈ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
≈ |
|
|
|
|
|
|
|
|
|
≈ $ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ≈ $ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
= |
= |
= = |
|
|
|
= |
|
|
||||||||||||||||||||||||||||||||||
* 8 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
89 % %= |
% % + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= + |
|
|
≈ |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
" = |
= − % %= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
! |
|
= |
|
|
|
− |
|
|
− |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= −
**
