
- •Часть 1. Дифференциальные уравнения первого порядка
- •Глава 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными
- •§ 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка.
- •1.1. Определение и формы записи дифференциального уравнения.
- •1.2. Определение решения ду. Поле направлений и изоклины уравнения. Задача Коши.
- •1.3. Теорема существования и единственности решения дифференциального уравнения вида для заданных начальных условий: .
- •§ 2. Уравнение 1-го порядка с разделяющимися переменными.
- •2.1. Формы записи дифференциального уравнения с разделяющимися переменными.
- •2.2. Простейшие задачи для дифференциальных уравнений 1-го порядка.
- •2.3. Решение дифференциальных уравнений 1-го порядка с разделяющимися переменными.
- •2.3.1. Решение ду 1-го порядка с разделяющимися переменными: .
- •2.3.2. Решение ду 1-го порядка с разделяющимися переменными: .
- •2.3.3. Решение ду 1-го порядка с разделяющимися переменными: .
- •2.3.4. Исследование особой точки (0,0) для ду 1-го порядка с разделяющимися переменными.
- •§ 4. Применение ду 1-го порядка с разделяющимися переменными: задачи из геометрии.
- •§ 5. Применение ду 1-го порядка с разделяющимися переменными: задачи из физики.
§ 4. Применение ду 1-го порядка с разделяющимися переменными: задачи из геометрии.
В общем
случае уравнение кривой
имеет вид:
![]() =0,
где
=0,
где
![]() − параметр семейства кривых.
Дифференциальное уравнение 1-го порядка
может быть записано в виде
− параметр семейства кривых.
Дифференциальное уравнение 1-го порядка
может быть записано в виде
![]() =0.
Геометрический смысл переменных
=0.
Геометрический смысл переменных
![]() − координаты произвольной точки кривой,
геометрический смысл производной
− координаты произвольной точки кривой,
геометрический смысл производной
![]() − тангенс угла наклона касательной в
точке
− тангенс угла наклона касательной в
точке
![]() .
.
На рисунке
представлена некоторая кривая
![]() =0.
Для произвольной точки
=0.
Для произвольной точки![]() этой кривой построены касательная
этой кривой построены касательная![]() и нормаль
и нормаль![]() и выделены точки пересечения касательной
и нормали с осями
и выделены точки пересечения касательной
и нормали с осями![]() и
и![]() ,
именно: а) для касательной: точки
,
именно: а) для касательной: точки![]() и
и![]() ;
б) для нормали: точки
;
б) для нормали: точки![]() и
и![]() .
.
П ростейшие
геометрические задачи с использованием
дифференциальных уравнений 1-го порядка
можно построить, записывая равенства
типа:
ростейшие
геометрические задачи с использованием
дифференциальных уравнений 1-го порядка
можно построить, записывая равенства
типа:![]() =
=![]() ,
где
,
где![]() произвольнаяфункция. Самый простой случай, когда
произвольнаяфункция. Самый простой случай, когда![]() =
=![]() .
.
В общем случае
рассматривают задачи, представляемые
равенствами, в которые входят длины
отрезков кривой:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и
и![]() – отрезки касательной,
– отрезки касательной,![]() – подкасательная,
– подкасательная,![]() и
и![]() – отрезки нормали,
– отрезки нормали,![]() – поднормаль. Каждое такое равенство
есть дифференциальное уравнение,
определяющее совокупные геометрические
свойства кривой. Решая уравнение, находят
соответствующее семейство кривых с
заданными свойствами. Задавая начальные
условия, из семейства кривых выделяют
единственную кривую.
– поднормаль. Каждое такое равенство
есть дифференциальное уравнение,
определяющее совокупные геометрические
свойства кривой. Решая уравнение, находят
соответствующее семейство кривых с
заданными свойствами. Задавая начальные
условия, из семейства кривых выделяют
единственную кривую.
Общая
задача. В соответствии с рисунком
определимхарактерные
отрезкикривой![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() обозначив угловой коэффициент касательной
в точке
обозначив угловой коэффициент касательной
в точке![]() величиной
величиной![]() .
.
Решение:
1). Запишем
уравнение касательной для точки
![]() :
: ![]() . (11)
. (11)
2). Запишем
уравнение нормали для точки
![]() :
: ![]() . (12)
. (12)
3).
Определим
координаты точек
![]() и
и
![]() пересечения касательной, представленной
в виде выражения (12),
с осями координат
пересечения касательной, представленной
в виде выражения (12),
с осями координат
![]() ,
,
![]() ;
вычислим
;
вычислим
![]() ,
,![]() :
:
а) для
точки
![]() имеем:
имеем:![]() =0
→
=0
→ ![]() =
=![]() →
→
![]() =
= →
→
![]() =
=![]() ;
(13)
;
(13)
б) для
точки
![]() имеем:
имеем:
![]() =0
→
=0
→ ![]() =
=![]() →
→
![]() =
=![]() →
→
![]() =
=![]() .
(14)
.
(14)
4).
Используя
(13)
и (14),
вычислим длины
отрезков
касательной
![]() и
и ![]() :
:
а)
![]() =
= –
–![]() =
= ;
;
![]() =
=![]() =
=![]() ; (15)
; (15)
б)
![]() =
=![]() –
–![]() =
=![]() ;
;
![]() =
=![]() =
=![]() . (16)
. (16)
5).
Используя
(13),
вычислим длину подкасательной: ![]() =
=![]() . (17)
. (17)
6).
Определим
координаты точек
![]() и
и
![]() пересечения нормали, представленной в
виде выражения (12),
с осями координат
пересечения нормали, представленной в
виде выражения (12),
с осями координат
![]() ,
,
![]() ;
вычислим
;
вычислим
![]() ,
,
![]() :
:
а) для
точки
![]() имеем:
имеем:![]() =0
→
=0
→ ![]() =
=![]() →
→
![]() =
=![]() →
→
![]() =
=![]() ;
(18)
;
(18)
б) для
точки
![]() имеем:
имеем:
![]() =0
→
=0
→ ![]() =
=![]() →
→
![]() =
=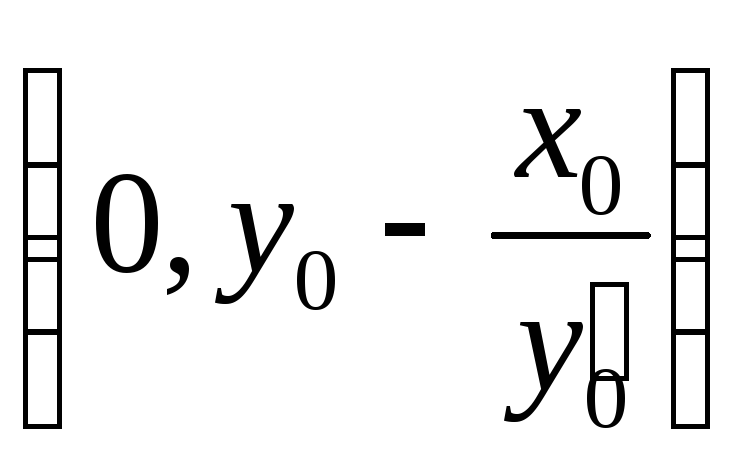 →
→
![]() =
=![]() .
(19)
.
(19)
7).
Используя
(13),
вычислим длины отрезков нормали![]() и
и
![]() :
:
а)
![]() =
=![]() –
–![]() =
=![]() ;
;
![]() =
=![]() =
=![]() ; (20)
; (20)
б)
![]() =
=![]() –
–![]() =
= ;
;
![]() =
=![]() =
=![]() . (21)
. (21)
8).
Используя
(16),
вычислим длину поднормали: ![]() =
=![]() .
.
Ответ: определены все характерные точки и отрезки произвольной кривой линии.
Замечание:
Формулы (11)![]() (21)
используют координаты выделенной точки
(21)
используют координаты выделенной точки
![]() ,
но записанные соотношения выполняются
для любой точки
,
но записанные соотношения выполняются
для любой точки
![]() кривой линии. При определении свойств
некоторой линии
кривой линии. При определении свойств
некоторой линии![]() мы будем использовать совокупные
свойства характерных
отрезков
мы будем использовать совокупные
свойства характерных
отрезков
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() по отношению ко всем её точкам! Это
значит, что в формулах (11)
по отношению ко всем её точкам! Это
значит, что в формулах (11)![]() (21)
индекс, отмечающий использование точки
(21)
индекс, отмечающий использование точки
![]() не должен применяться!
не должен применяться!
☺☺
Пример 1–20:
Найти
уравнение кривой, проходящей через
точку
![]() ,
зная, что длина отрезка
,
зная, что длина отрезка
![]() ,
который отсекает касательная в
произвольной точке кривой на оси ординат,
равна удвоенной длине ординаты
,
который отсекает касательная в
произвольной точке кривой на оси ординат,
равна удвоенной длине ординаты ![]() точки касания.
точки касания.
Замечание: При решении частных геометрических задач с применением дифференциальных уравнений 1-го порядка рекомендуем распечатать фрагмент настоящего Пособия от заголовка § 4 до символов: ☺☺ и применять как справочный материал. В приводимых ниже Примерах в условии конкретной задачи используются обозначения отрезков в соответствии с рисунком Общей задачи. Формулы, полученные в Общей задача и используемые в конкретной задаче, применять без доказательства, но внимательно прочитывая соответствующий фрагмент Общей задачи!..
Решение:
1 ).
Используя результаты Общей задачи,
запишем в виде формулы условие задачи:
).
Используя результаты Общей задачи,
запишем в виде формулы условие задачи:
![]() =2
=2![]() .
Так как произвольная точка кривой
обозначается как
.
Так как произвольная точка кривой
обозначается как
![]() ,
то
,
то
![]() =
=![]() и
и
![]() =
=![]() .
На рисунке (для формирования зрительного
образа задачи!) отрезки
.
На рисунке (для формирования зрительного
образа задачи!) отрезки
![]() и
и
![]() выделены красным цветом: рисунок отражает
фрагмент одной из возможных кривых
линий с выделенной касательной в
произвольной точке.
выделены красным цветом: рисунок отражает
фрагмент одной из возможных кривых
линий с выделенной касательной в
произвольной точке.
2). Модульное равенство предполагает два случая записи условия (значит, и два случая решения) задачи:
▪ Случай-1:
![]() ;
; ![]()
▪ Случай-2:
![]() .
. ![]()
Случай-1.
1 .1.
Отметим, что в соответствии с записью
.1.
Отметим, что в соответствии с записью
![]() уравнение не может иметь решение
уравнение не может иметь решение
![]() .
Решение
.
Решение
![]() возможно, но не отражает существа
решаемой задачи: назовём его тривиальным.
Принимая
возможно, но не отражает существа
решаемой задачи: назовём его тривиальным.
Принимая
![]() и
и
![]() ,
запишем уравнение
,
запишем уравнение
![]() в виде:
в виде:
![]() – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
1.2. Общее
решение для этого уравнения представим
в виде: ![]() ,
которое получено в предположении, что
,
которое получено в предположении, что![]() .
.
1.3. Учитывая
свойства произвольной постоянной
величины, общее решение запишем в виде:
![]() ,
ещё лучше в виде записи, используемой
в элементарной алгебре:
,
ещё лучше в виде записи, используемой
в элементарной алгебре:
![]() –семейство
гипербол. На рисунке показаны
интегральные кривые для случая
–семейство
гипербол. На рисунке показаны
интегральные кривые для случая![]() >0
и для случая
>0
и для случая![]() <0.
Второе семейство кривых получаем из
первого семейства кривых линий при
помощи зеркального отображения
относительно оси
<0.
Второе семейство кривых получаем из
первого семейства кривых линий при
помощи зеркального отображения
относительно оси![]() .
.
1.4.
Учитывая
начальные условия: кривая должна
проходить через точку
![]() ,
выделим частное решение уравнения. Из
равенства
,
выделим частное решение уравнения. Из
равенства
![]() вычисляем
вычисляем
![]() =1,
что выделяет из семейства интегральных
кривых ту, которая проходит через точку
=1,
что выделяет из семейства интегральных
кривых ту, которая проходит через точку
![]() :
на рисунке эта кривая выделена, именно
:
на рисунке эта кривая выделена, именно
![]() .
.
Случай-2.
1.1. Как
и в Случае-1, в соответствии с записью
![]() уравнение не может иметь решение
уравнение не может иметь решение
![]() .
Решение
.
Решение
![]() возможно, но не отражает существа
решаемой задачи: назовём его тривиальным.
Принимая
возможно, но не отражает существа
решаемой задачи: назовём его тривиальным.
Принимая
![]() и
и
![]() ,
запишем уравнение
,
запишем уравнение
![]() в виде:
в виде:
![]() – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
1.2. Общее
решение для этого уравнения представим
в виде: ![]() ,
которое получено в предположении, что
,
которое получено в предположении, что![]() .
.
1.3. Учитывая
свойства произвольной постоянной
величины, общее решение запишем в виде:
![]() –семейство
кубических парабол. На рисунке
показаны интегральные кривые для случая
–семейство
кубических парабол. На рисунке
показаны интегральные кривые для случая![]() >0
и для случая
>0
и для случая![]() <0.
Второе семейство кривых получаем из
первого семейства кривых линий при
помощи зеркального отображения
относительно оси
<0.
Второе семейство кривых получаем из
первого семейства кривых линий при
помощи зеркального отображения
относительно оси![]() .
.
1 .4.Учитывая
начальные условия: кривая должна
проходить через точку
.4.Учитывая
начальные условия: кривая должна
проходить через точку
![]() ,
выделим частное решение уравнения. Из
равенства
,
выделим частное решение уравнения. Из
равенства
![]() вычисляем
вычисляем
![]() =1,
что выделяет из семейства интегральных
кривых ту, которая проходит через точку
=1,
что выделяет из семейства интегральных
кривых ту, которая проходит через точку
![]() :
на рисунке эта кривая выделена, именно
:
на рисунке эта кривая выделена, именно
![]() .
.
Ответ:
общее решение:
Случай-1
![]() ,
Случай-2:
,
Случай-2:
![]() ;
частные решения:
;
частные решения:
![]() и
и
![]() ,
соответственно Решения уравнения:
,
соответственно Решения уравнения:
![]() и
и
![]() отнесены к тривиальным решениям: теряют
привычный геометрический смысл и не
представляют для нас никакого интереса!
отнесены к тривиальным решениям: теряют
привычный геометрический смысл и не
представляют для нас никакого интереса!
☻
Замечание: Учитывая результаты решения Общей задачи в начале настоящего параграфа, а также детально разобранный Пример, иллюстрирующий применение дифференциальных уравнений 1-го порядка с разделяющимися переменными в геометрических задачах, рекомендуем каждому студенту самостоятельно построить Пример и решить его. Это поможет ещё больше прочувствовать и оценить возможности дифференциальных уравнений в инженерной практике!..
