14.3. Приведение общего уравнения кривой второго порядка к каноническому виду

Пусть на плоскости задана декартова система координат (декартов базис , и точкаО– начало координат). Рассмотрим общее уравнение 2-го порядка:

. (14.25)

Обозначим через сумму старших слагаемых:

и рассмотрим квадратичную форму

.

Ее матрица симметрическая.

Пусть - произвольное евклидово пространство,,- линейный оператор вс матрицейв базисе,, следовательно,- самосопряженный оператор в. Тогда существует ортонормированный базис, состоящий из собственных векторов оператора(см. лекцию 13, § 13.3, теорема 9), в этом базисе матрица операторадиагональная и имеет вид, где- собственные значения (см. § 12.3).

Если матрица перехода от базиса ,к базису, то(см. § 12.2).

Рассмотрим теперь линейное преобразование неизвестных с матрицей :. Квадратичная форма от новых неизвестныхимеет вид, где.

Итак, если - ортонормированный базис из собственных векторов оператора, матрицакак матрица перехода от ортонормированного базиса к ортонормированному ортогональна () , следовательно, матрица квадратичной формы от неизвестныхдиагональная и.

Такой способ приведения квадратичной формы к каноническому виду называется методом собственных векторов.

Пример 4. Привести квадратичную форму к каноническому виду методом собственных векторов.

Матрица квадратичной формы имеет вид. Рассмотрим в произвольном евклидовом пространстве,, линейный операторс матрицейв некотором ортонормированном базисе. Найдем его собственные векторы.

Характеристическое уравнение ,, его корни,.

Имеем для :и,;

для :и,.

Положим ,и получим,.

В базисе ,матрица операторадиагональная:. Нормируем векторыи:и,.

Матрица перехода от базиса ,к базису,. Вернемся к квадратичной форме. Положим, т.е.

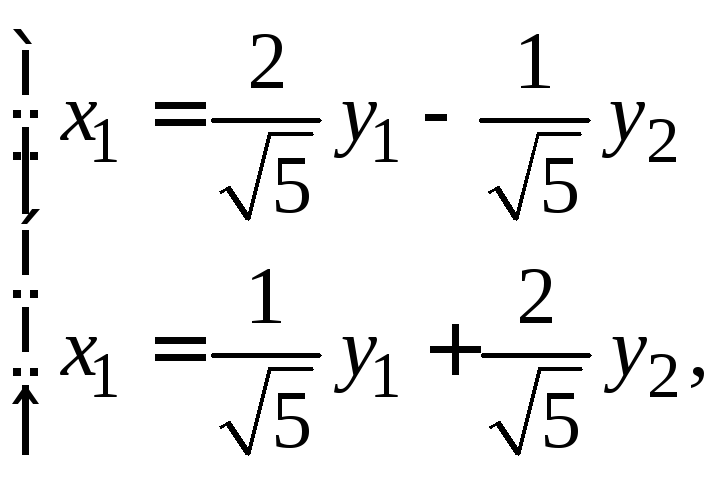(14.26)

Тогда .

Замечание.Формулы (14.26) – формулы поворота осей координат на уголпротив хода часовой стрелки. Уголопределяется соотношениями

,().

В общем случае преобразование поворота

(14.27)

приведет линию (14.25) к виду

. (14.28)

Эта процедура называется приведением линии 2-го порядка к главным осям (из дальнейшего изложения будет ясно, что, если (14.25) – эллипс или гипербола, новые оси ипараллельны главным осям кривой).

Коэффициенты ив уравнении (14.28) – характеристические числа матрицыи могут быть найдены как корни уравнения, или

. (14.29)

Обозначим ,.

Имеем (действительно, из (14.29) находим, или, и по теореме Виета).

Случай 1.(кривая эллиптического типа).

Преобразуем (14.28) следующим образом:

,

или, обозначив , придем к равенству

.

Положим 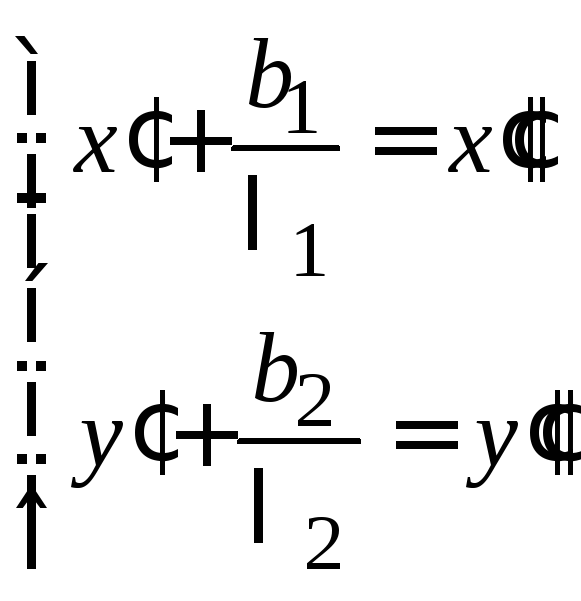(14.30)

и в новой системе координат имеем

. (14.31)

Формулы (14.30) – формулы параллельного переноса начала координат в точку .

Случай 1. а) Знакпротивоположен знаку(и, следовательно, знаку). Тогда (14.31) определяет эллипс:

;

б) , уравнение (14.31) определяет одну точку:;

в) Знаки исовпадают, нет точек (мнимый эллипс).

Случай 2.(кривая гиперболического типа).

В этом случае знаки ипротивоположны.

а) , уравнение (14.31) определяет гиперболу:

;

б) , уравнение (14.31) принимает вид:

.

Пусть , тогдаи уравнение (14.31) можно переписать в следующем виде:

. (14.32)

Уравнение (14.32) определяет пару пересекающихся прямых: .

Случай 3.(кривая параболического типа).

Пусть для определенности (тогда).

Уравнение (14.25) преобразованием (14.27) приводится к виду

. (14.33)

Пусть , тогда (14.33) можно переписать следующим образом:

.

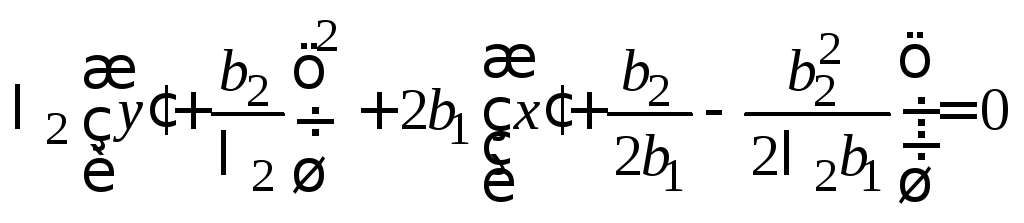Получим 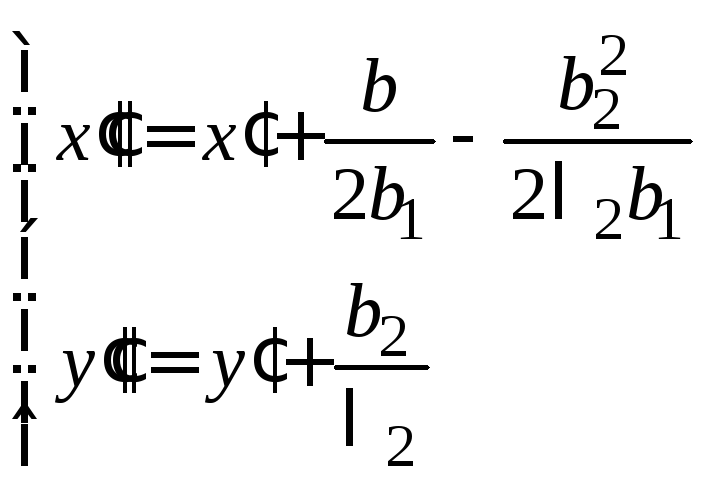и

. (14.34)

Уравнение (14.34) определяет параболу.

Если же , то уравнение (14.33) перепишем в виде

.

Обозначив и положив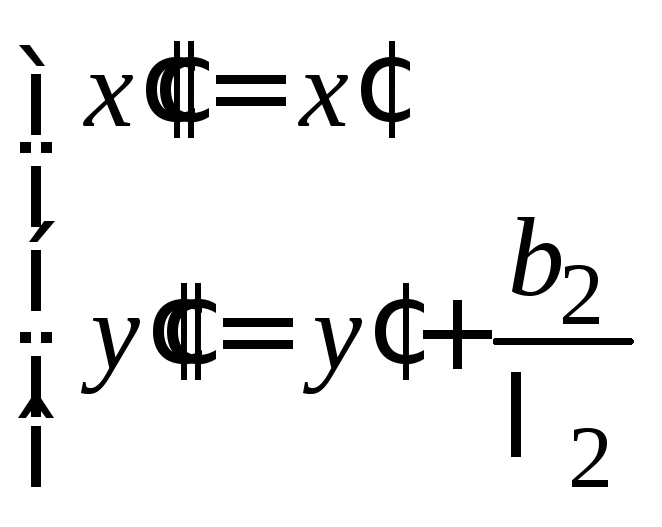, придем к уравнению

. (14.35)

а) , уравнение (14.35) определяет пару параллельных прямых:.

б) , уравнение (14.35) определяет пару совпадающих прямых:.

в) , нет точек (пара мнимых прямых).

Сведем полученные результаты в таблицу:

Кривая эллиптического типа		иразных знаков	Эллипс
		иодного знака	Мнимый эллипс
			Точка
Кривая гиперболического типа			Гипербола
			Пара пересекающихся прямых
Кривая параболического типа		иодного знака	Пара мнимых параллельных прямых
		иразных знаков	Пара параллельных прямых
			Пара совпадающих прямых
			Парабола

Пример 5. Определить вид и расположение кривой 2-го порядка

. (14.36)

Слагаемые 2-го порядка в (14.36) составляют квадратичную форму

,

которую преобразование неизвестных по формулам

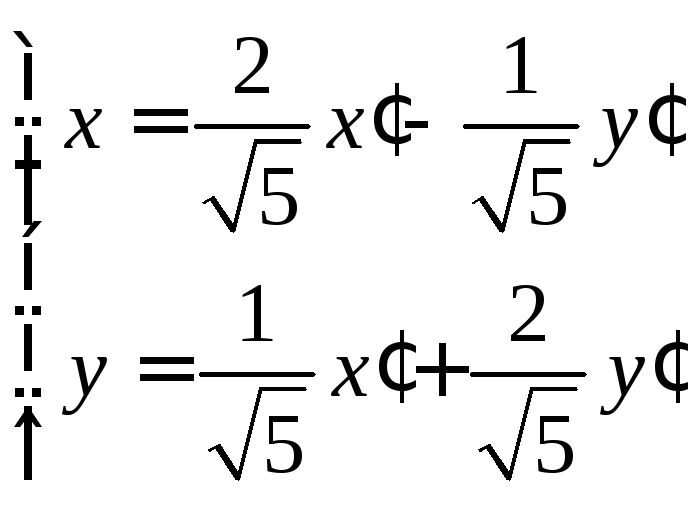(14.37)

приводит к сумме квадратов (пример 4).

Тогда уравнение кривой (14.36) преобразованием (14.37) приводится к виду

.

Здесь ,и, следовательно,, кривая эллиптического типа.

Как в случае 1, соберем слагаемые, содержащие неизвестное и дополним их до полного квадрата, аналогично поступим со слагаемыми, содержащими:

, или

Положим и получим

. (14.38)

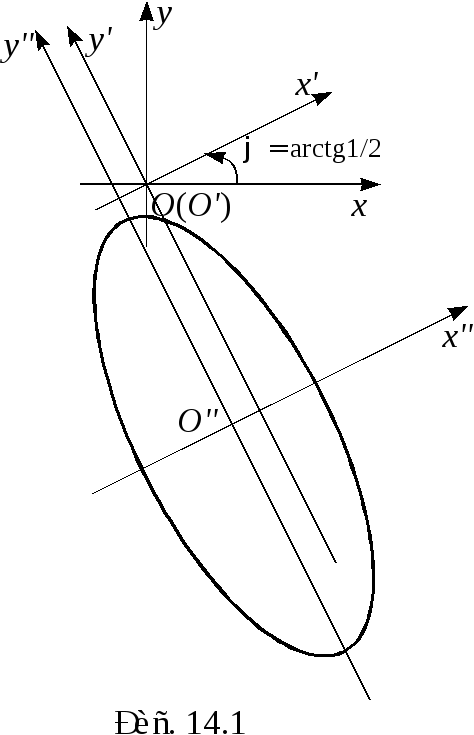
Уравнение (14.38) – уравнение эллипса с полуосями и центром в точке. Рис. 14.1 - схематический рисунок кривой.

195