Лекция 11

Связь между базисами линейного пространства.

Линейные подпространства

Матрица перехода от базиса к базису. Связь координат одного и того же вектора в двух базисах. Линейные подпространства. Примеры

11.1. Связь между базисами линейного пространства

Пусть - линейное пространство, (I) и (II) - два базиса в .

Так как (I) - базис, любой вектор из , в частности любой вектор системы (II), можно представить в виде линейной комбинации векторов системы (I), т.е. найдутся такие числа , что

………………………………. (11.1)

Определение 1. Матрица называется матрицей перехода от базиса (I) к базису (II).

Замечание 1. Столбцы матрицы перехода , являются координатами в разложении векторов по базису (I).

Справедливость этого замечания непосредственно следует из равенств (11.1).

Замечание 2. Матрица перехода от базиса к базису является невырожденной матрицей.

Доказательство этого факта опустим.

Справедливо следующее утверждение.

Теорема 1. Пусть - линейное пространство, (I) и (II) - два базиса в , - матрица перехода от (I) к (II), , и , тогда

. (11.2)

Доказательство. Подставим в разложение по базису (II) выражения из (11.1), получим

.

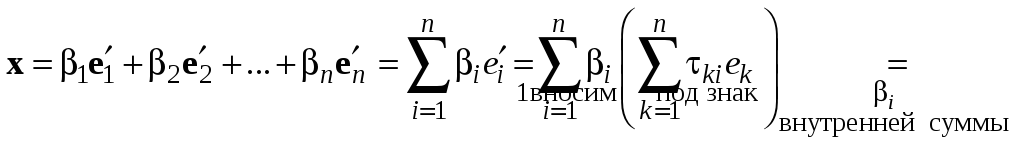
Последнюю сумму запишем развернуто:

.

По условию , используя теорему о единственности разложения вектора по базису (теорема 3 в лекции 10), получим

,

,

……………………………………

,

что в матричном виде выглядит как равенство

.

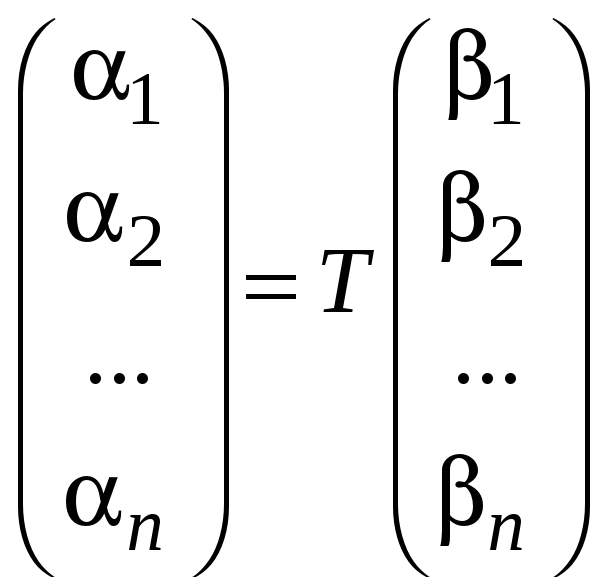Отсюда следует

.

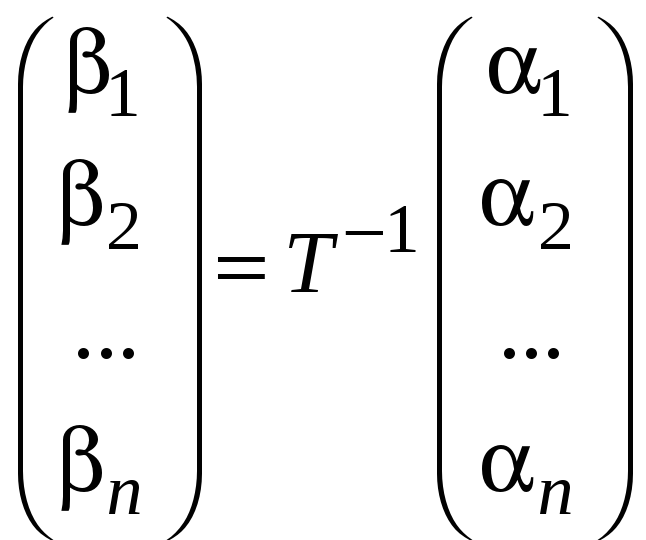Теорема доказана.

Пример 1. - линейное пространство всех геометрических векторов плоскости, (I) - произвольный декартов базис, (II) - декартов базис, полученный поворотом векторов и на угол против хода часовой стрелки. Найти матрицу перехода от (I) к (II) и связь координат одного и того же вектора в (I) и (II).

Имеем , (рис. 11.1). Тогда

.

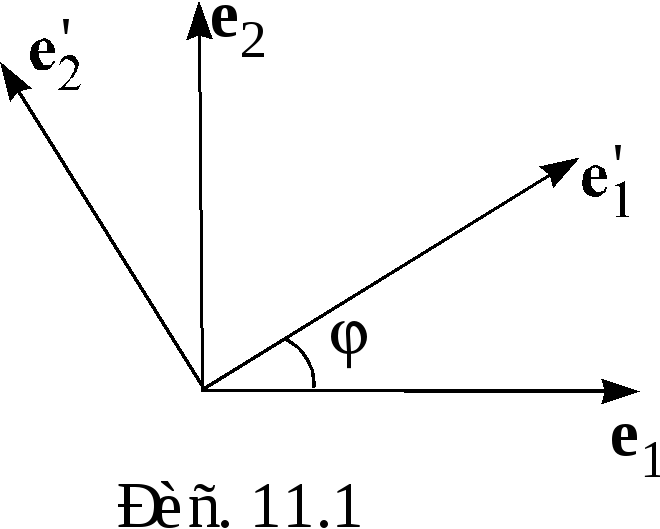- матрица перехода от (I) к (II).

Найдем .

и

.

Формула (11.2) в этом случае имеет вид

,

где - координаты произвольного вектора в базисе (I), а – координаты этого же вектора в базисе (II).

(Сравните с формулами (5.24) в Лекции 5).

Пример 2. - произвольное линейное пространство, . Векторы , и заданы своими координатами в некотором базисе . Доказать, что система - базис в , и найти координаты вектора в базисе .

Сначала докажем, что система - базис. Рассмотрим линейную комбинацию векторов и , равную нулевому вектору :

.

Покоординатно последнее равенство запишется в виде системы двух уравнений:

(11.3)

Определитель системы (11.3) , следовательно, система (11.3) имеет единственное решение .

Итак, допустив, что линейная комбинация векторов и равна , мы с необходимостью получили, что коэффициенты этой линейной комбинации равны нулю. Это означает, что система векторов линейно независима, а так как , векторы являются базисом в . Обозначим этот базис (II).

Найдем матрицу перехода от (I) к (II).

В силу определения 1 (координаты векторов и в (I) располагаем по столбцам).

Обозначим через координаты вектора в (II).

Воспользуемся теоремой 1. Найдем . Имеем

,

и по формуле (11.2) получим

.

Итак, .

Упражнения.

1. - линейное пространство многочленов степени . Доказать, что система многочленов образует базис в . Найти матрицу перехода от базиса 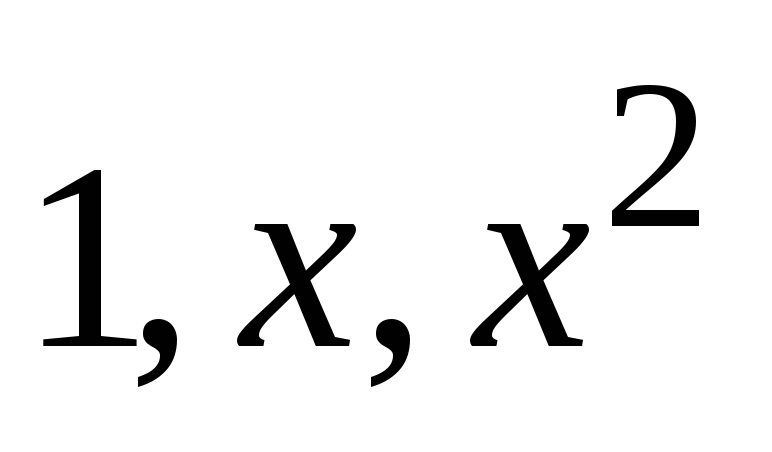к этому базису и координаты многочлена 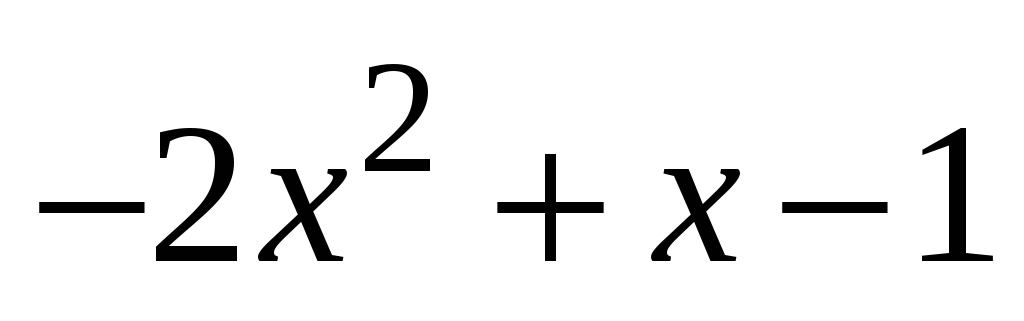в нем.

2. В произвольном линейном пространстве векторы и заданы своими координатами в некотором базисе : , , , . Доказать, что система векторов - базис в , и найти координаты в этом базисе.

3. В произвольном линейном пространстве векторы (I) и (II) заданы своими координатами в некотором базисе , , , , , . Доказать, что системы (I) и (II) являются базисами в , и найти матрицу перехода от (I) к (II).

11.2. Линейные подпространства

Определение 2. Пусть - линейное пространство. Непустое подмножество линейного пространства () называется линейным подпространством в , если выполняются два условия:

1) ;

2) при любом вещественном числе .

Пример 3. Пусть - линейное пространство всех арифметических -мерных векторов ; - совокупность всех векторов, у которых первая и последняя компоненты равны нулю, т.е. векторов вида . - подпространство в .

Действительно, пусть и , следовательно, по определению и . По правилу сложения векторов в и, таким образом, сумма любых двух векторов из принадлежит .

Пусть и - произвольное вещественное число. Но (так как ), следовательно, по правилу умножения вектора на число в и вместе с любым вектором произведение его на тоже принадлежит . В соответствии с определением 2 это означает, что - линейное подпространство в .

Замечание. Если - линейное подпространство в , то само является линейным пространством относительно введенных в операций сложения и умножения на число.

Действительно, требования 1) и 2) в определении 2 означают, что в определены операции сложения векторов и умножения вектора на число.

Аксиомы 1 и 2 выполняются в , так как они имеют место в . Убедимся в справедливости аксиомы 3.

Пусть , , следовательно, согласно условию 2) , но по следствию 5 из аксиом в , таким образом, и в справедлива аксиома 3.

Пусть , . Следовательно, согласно условию 2) , но по следствию 8 из аксиом в , таким образом, и в справедлива аксиома 4.

Аналогично проверяется справедливость аксиом 5 - 8, следовательно, - линейное пространство.

Пусть - произвольное линейное пространство, - некоторая система векторов в . Рассмотрим совокупность всех векторов вида , где принимают всевозможные вещественные значения. Обозначим множество этих векторов . называется линейной оболочкой векторов . является подпространством в .

Действительно, (так как, например, сами векторы , , принадлежат ).

Пусть , , следовательно, по определению такие, что , .

Имеем и .

Пусть , - произвольное вещественное число.

Имеем

и .

Таким образом, выполняются условия 1) и 2) определения 2 и является линейным подпространством в .

Говорят, что порождено системой векторов или "натянуто" на систему .

Заметим, что само линейное пространство может рассматриваться как линейная оболочка любого своего базиса.

Пример 4. Найти размерность и базис линейной оболочки векторов , , .

Найдем ранг матрицы, строками которой являются данные векторы , , :

~~.

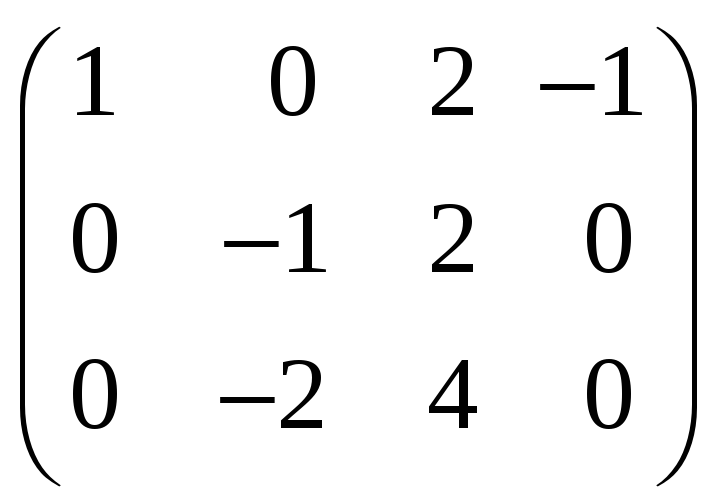Минор второго порядка , следовательно, первые две строки матрицы линейно независимы. Значит, векторы и составляют линейно независимую систему векторов в , а следовательно, и в линейной оболочке , и вектор через них линейно выражается. Тогда любой вектор тоже линейно выражается через и . Векторы и являются базисом в , .

Упражнение. - линейное пространство арифметических векторов . Найти размерность и все базисы линейной оболочки векторов , , , .

143