1.2. Линейная зависимость векторов

Линейной комбинациейвекторовс коэффициентамибудем называть сумму

.

Определение 5.Векторы называются линейно зависимыми, если найдутся такие числа, не все равные нулю одновременно, что

(линейная комбинация векторов с коэффициентамиравна нулевому вектору).

Пример.Вектори его противоположный векторсоставляют линейно зависимую систему векторов.

Действительно, (см. замечание 4). Таким образом,

и система линейно зависима.

Определение 6.Система векторов называется линейно независимой, если из равенства следует, что.

Теорема 1.Система векторов, содержащая нулевой вектор , линейно зависима.

Доказательство.Пусть в системе вектороввектор,. Рассмотрим линейную комбинацию, причем среди коэффициентов не все равны нулю (). Следовательно, в соответствии с определением 5 системалинейно зависима.

Теорема 2.Всякая система векторов , содержащая линейно зависимую подсистемувекторов,, линейно зависима.

Доказательство.Пусть для определенности линейно зависимы первыевекторов(это допущение не ограничивает общности рассуждений, так как мы могли бы перенумеровать всю исходную систему, если бы были линейно зависимы другие векторы).

Это означает, что найдутся числа , не все равные нулю, и такие что

.

Но линейная комбинация всей системы векторовс коэффициентамиравна:

.

Следовательно, система линейно зависима.

Теоремы 3 - 5 проясняют понятие линейной зависимости для геометрических векторов.

Теорема 3.Необходимым и достаточным условием линейной зависимости двух геометрических векторов является их коллинеарность.

Доказательство.Необходимость.Пустьилинейно зависимы. Тогда существуют числаи(хотя бы одно из которых не равно нулю), что.

Пусть для определенности , тогда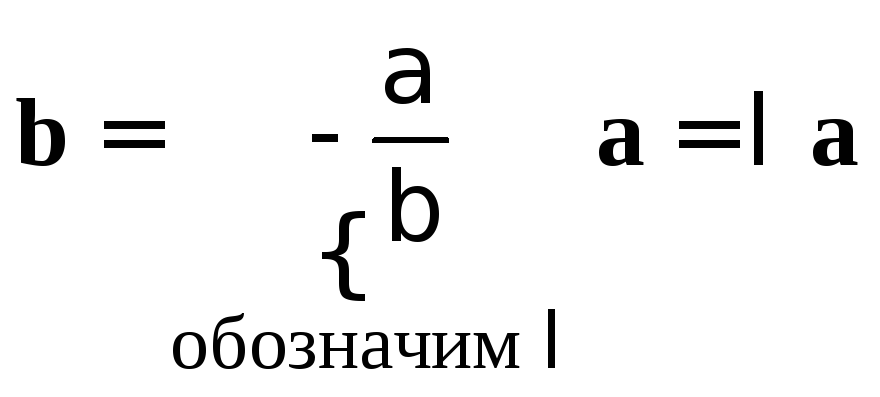, и один из векторов оказался равен произведению другого на число, следовательно (см. определение 4), векторыиколлинеарны.

Обратно.Пусть векторыиколлинеарны.

Случай 1.Хотя бы один из векторов нулевой:(либо, либо), тогда (см. теорему 1) система,линейно зависима.

Случай 2.,. В силу замечания 5 найдется числотакое, что, следовательно,и линейная комбинация векторовис коэффициентами, не равными нулю одновременно, равна нулевому вектору, – это означает, что система,линейно зависима.

Следствие.Если два вектораине коллинеарны, они линейно независимы (допустим противное, тогдаиколлинеарны (Теор. 3), что противоречит условию).

Определение 7.Векторы называются компланарными, если они лежат в одной или параллельных плоскостях (рис. 1.13).

Теорема 4.Необходимым и достаточным условием линейной зависимости трех геометрических векторов является их компланарность.

Доказательство.Необходимость.Пусть векторы,илинейно зависимы. Тогда существуют такие числа,,, не все равные нулю, что выполняется равенство

.

Пусть для определенности (это допущение не ограничивает общности рассуждений, совершенно аналогично рассматриваются случаилибо). Тогда

(1.6)

Пусть ,иприложены к одному началу.

Равенство (1.6) означает, что вектор совпадает с диагональю параллелограмма, построенного на векторахи, а, следовательно, лежит в плоскости этого параллелограмма, тогда все три вектора,илежат в этой плоскости, т. е. они компланарны.

Достаточность.Пусть,икомпланарны.

Случай 1.В системе векторов,,присутствует нулевой вектор, следовательно (см. теорему 1), система,,линейно зависима.

Случай 2.,,и какая-нибудь пара из векторов,,коллинеарна, следовательно (см. теорему 3), эта пара составляет линейно зависимую подсистему в системе,,, тогда вся система,,линейно зависима (см. теорему 2).

Случай 3.,,и никакие два из них не коллинеарны.

Приведем ,ик одному началу – некоторой точкеи через конец векторапроведем прямые, соответственно параллельныеи, получим точкии(рис. 1.14). Имеем

(1.7)

Вектор коллинеарен вектору, следовательно (см. замечание 5), найдется число:. Аналогично векторколлинеарен, следовательно, найдется число:.

Таким образом, равенство (1.7) примет вид , откуда получим

,

что означает линейную зависимость системы ,,.

Следствие 1.Пусть ине коллинеарны, тогда любой вектор плоскости можно представить в виде их линейной комбинации (см. доказательство достаточности, случай 3).

Следствие 2.Если три вектора ,и не компланарны, они линейно независимы (допустим противоположное, тогда по теореме 4,,компланарны, что противоречит условию).

Теорема 5.Любые четыре геометрических вектора линейно зависимы.

Доказательство.Пусть,,и– рассматриваемые векторы.

Случай 1.Какие-нибудь три из четырех векторов компланарны, тогда (см. теорему 4), эти три вектора линейно зависимы, следовательно (см. теорему 2), все четыре вектора линейно зависимы, так как содержат зависимую подсистему.

Случай 2.Среди четырех векторов,,иникакие три не компланарны.

Приведем векторы ,,ик одному началуи проведем через конец вектораплоскости, соответственно параллельные плоскостям, определяемым парами векторови,и,и.

Точки пересечения этих плоскостей с прямыми, на которых лежат ,и, обозначим,исоответственно (рис. 1.15).

Из параллелограмма , аналогично из параллелограммаи, таким образом,

. (1.8)

Вектор коллинеарен, следовательно, найдется числотакое, что

.

Вектор коллинеарен, следовательно, найдется числотакое, что

.

Вектор коллинеарен, следовательно, найдется числотакое, что

.

Подставив полученные результаты в (1.8), найдем

,

или

. (1.9)

Равенство (1.9) означает линейную зависимость векторов ,,и: их линейная комбинация с коэффициентами, не равными нулю одновременно (коэффициент приравени отличен от нуля), равна.

Следствие.Каковы бы ни были некомпланарные векторы ,и, любой вектор можно представить в виде их линейной комбинации