
- •Аннотация
- •Оглавление
- •Предисловие
- •ГЛАВА 1. Задачи оптимизации. Основные определения
- •1.1. Задачи оптимизации
- •1.2. Минимум функции одной переменной
- •1.3. Унимодальные функции
- •1.4. Выпуклые функции
- •1.5. Условие Липшица
- •1.6. Классическая минимизация функции одной переменной
- •Вопросы и задания для самоконтроля
- •ГЛАВА 2. Одномерная минимизация функций. Прямые методы
- •2.1. О прямых методах
- •2.2. Метод перебора
- •2.3. Метод поразрядного поиска
- •2.4. Метод дихотомии
- •2.5. Метод золотого сечения
- •2.6. Сравнение методов перебора, дихотомии и золотого сечения
- •2.7. Метод парабол
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 3. Одномерная минимизация. Методы, использующие информацию о производных целевой функции
- •3.1. Метод средней точки
- •3.2. Метод хорд
- •3.3. Метод Ньютона
- •3.4. Возможные модификации метода Ньютона
- •3.5. Методы минимизации многомодальных функций
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 4. Задача минимизации функции многих переменных. Необходимые и достаточные условия безусловного экстремума
- •4.1. Постановка задачи и определения
- •4.2. Свойства выпуклых множеств и выпуклых функций
- •4.3. Необходимые и достаточные условия безусловного экстремума
- •Вопросы и задания для самоконтроля
- •5.1. Выпуклые квадратичные функции
- •5.2. Общие принципы многомерной минимизации
- •5.3. Метод градиентного спуска
- •5.4. Метод наискорейшего спуска
- •5.5. Метод сопряженных направлений
- •5.6. Метод сопряженных градиентов
- •5.7. Метод Ньютона
- •5.8. Квазиньютоновские методы
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 6. Прямые методы безусловной минимизации многомерных задач
- •6.1. Проблема минимизации многомерных задач
- •6.2. Минимизация функций по правильному (регулярному) симплексу
- •6.3. Минимизация функций при помощи нерегулярного симплекса
- •6.4. Метод циклического покоординатного спуска
- •6.5. Метод Хука–Дживса
- •6.6. Методы случайного поиска
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •7.1. Условный экстремум при ограничениях типа равенств
- •7.2. Условный экстремум при ограничениях типа неравенств
- •Вопросы и задания для самопроверки
- •ГЛАВА 8. Линейное программирование
- •8.1. Определения. Примеры задач линейного программирования
- •8.2. Общая и каноническая задачи линейного программирования
- •8.3. Геометрическое истолкование задач линейного программирования
- •8.4. Аналитическое решение задач линейного программирования
- •Вопросы и задания для самоконтроля
- •Литература
dx |
2 |
≠ 0 |
, а λ = − |
1 |
< 0 , то достаточные условия максимума не выполняются. Так как |
|||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d 2 L(B) ≥ 0 |
при всех dx2 , то и необходимое условие максимума второго порядка в |
|||||||||||||||||||||
точке |
B |
не |
|
|
выполняется. |
Поэтому |
в |
ней нет |
экстремума. |
Так как |
||||||||||||
|
2 |
|
|
|
|
3 |
|
|
2 |
2 |
|
|
при dx2 ≠ 0 , |
то |
достаточные условия |
максимума |
||||||
d |
|
L(C) = − (− |
|
)dx2 |
− dx2 < 0 |
|||||||||||||||||
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выполняются. В точке C условный локальный максимум. |
|
|
||||||||||||||||||||
|
|
|
5. Вычислим значения функций в точках экстремума |
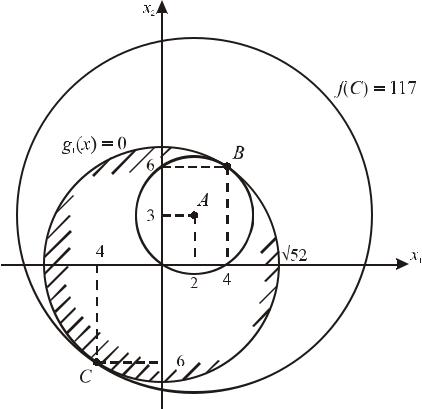
f ( A) = 0, f (C) =117 . |
||||||||||||||||||
|
|
|
Графическое решение задачи приведено на рис.7.9. ■ |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.7.9. Графическое решение задачи из примера 7.10
Вопросы и задания для самопроверки
1.Что называется обобщенной (классической) функцией Лагранжа задачи условного экстремума?
2.Что называется градиентом обобщенной (классической) функции Лагранжа?
3.Что называется вторым дифференциалом обобщенной (классической) функции Лагранжа?
4.Что называется первым дифференциалом ограничения g j (x) ?
149
5.Когда ограничение g j (x) ≤ 0 называется активным в точке x ?
6.Когда ограничение g j (x) ≤ 0 называется пассивным в точке x ?
7.При каких условиях градиенты ограничений g1 (x), ..., gm (x) называются
линейно зависимыми в точке x , линейно независимыми в точке x ?
8.Сформулировать необходимые условия экстремума первого порядка с ограничениями типа равенств.
9.Какие точки x называются условно-стационарными в задаче экстремума с ограничениями типа равенств?
10.Какие точки экстремума x называются регулярными, а какие − нерегулярными при ограничениях типа равенств?
11.В каком случае антиградиент целевой функции является линейной комбинацией градиентов ограничений?
12.Сформулировать необходимые условия экстремума второго порядка; достаточные условия экстремума в случае ограничений типа равенств.
13.В каких точках x проверяются необходимые условия второго порядка и достаточные условия в случае ограничений типа равенств?
14.Сформулировать алгоритм решения задачи нахождения экстремума в случае ограничений типа равенств.
15.Сформулировать необходимые условия минимума (максимума) первого порядка с ограничениями типа неравенств.
16.В каком случае необходимые условия минимума (максимума) первого порядка с ограничениями типа неравенств являются одновременно и достаточными условиями минимума (максимума)?
17.Сформулировать достаточные условия минимума (максимума) первого порядка в случае ограничений типа неравенств.
18.Сформулировать необходимое условие минимума (максимума) второго порядка в случае ограничений типа неравенств.
19.Сформулировать достаточные условия экстремума второго порядка в случае ограничений типа неравенств.
20.Сформулировать алгоритм решения задачи нахождения экстремума в случае ограничений типа неравенств.
150
