
- •Аннотация
- •Оглавление
- •Предисловие
- •ГЛАВА 1. Задачи оптимизации. Основные определения
- •1.1. Задачи оптимизации
- •1.2. Минимум функции одной переменной
- •1.3. Унимодальные функции
- •1.4. Выпуклые функции
- •1.5. Условие Липшица
- •1.6. Классическая минимизация функции одной переменной
- •Вопросы и задания для самоконтроля
- •ГЛАВА 2. Одномерная минимизация функций. Прямые методы
- •2.1. О прямых методах
- •2.2. Метод перебора
- •2.3. Метод поразрядного поиска
- •2.4. Метод дихотомии
- •2.5. Метод золотого сечения
- •2.6. Сравнение методов перебора, дихотомии и золотого сечения
- •2.7. Метод парабол
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 3. Одномерная минимизация. Методы, использующие информацию о производных целевой функции
- •3.1. Метод средней точки
- •3.2. Метод хорд
- •3.3. Метод Ньютона
- •3.4. Возможные модификации метода Ньютона
- •3.5. Методы минимизации многомодальных функций
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 4. Задача минимизации функции многих переменных. Необходимые и достаточные условия безусловного экстремума
- •4.1. Постановка задачи и определения
- •4.2. Свойства выпуклых множеств и выпуклых функций
- •4.3. Необходимые и достаточные условия безусловного экстремума
- •Вопросы и задания для самоконтроля
- •5.1. Выпуклые квадратичные функции
- •5.2. Общие принципы многомерной минимизации
- •5.3. Метод градиентного спуска
- •5.4. Метод наискорейшего спуска
- •5.5. Метод сопряженных направлений
- •5.6. Метод сопряженных градиентов
- •5.7. Метод Ньютона
- •5.8. Квазиньютоновские методы
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 6. Прямые методы безусловной минимизации многомерных задач
- •6.1. Проблема минимизации многомерных задач
- •6.2. Минимизация функций по правильному (регулярному) симплексу
- •6.3. Минимизация функций при помощи нерегулярного симплекса
- •6.4. Метод циклического покоординатного спуска
- •6.5. Метод Хука–Дживса
- •6.6. Методы случайного поиска
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •7.1. Условный экстремум при ограничениях типа равенств
- •7.2. Условный экстремум при ограничениях типа неравенств
- •Вопросы и задания для самопроверки
- •ГЛАВА 8. Линейное программирование
- •8.1. Определения. Примеры задач линейного программирования
- •8.2. Общая и каноническая задачи линейного программирования
- •8.3. Геометрическое истолкование задач линейного программирования
- •8.4. Аналитическое решение задач линейного программирования
- •Вопросы и задания для самоконтроля
- •Литература
7.2. Условный экстремум при ограничениях типа неравенств
Пусть требуется исследовать функцию f (x) на экстремум, т.е. определить
точки x U ее локальных минимумов и максимумов
|
f (x ) = min f (x) , |
f (x ) = max f (x) , |
(7.11) |
|||
|
U = {x : g j (x) ≤ 0, |
x U |
x U |
|
|
|
где |
j =1, ..., m}. |
Рассмотрим |
условный |
экстремум |
с |
|
ограничениями типа неравенств. |
|
|
|
|
||
|
Стратегия решения задачи |
|
|
|
|
|
|
Находятся точки |
x локального |
экстремума |
с помощью |
необходимых |
и |
достаточных условий минимума и максимума первого и второго порядка при ограничениях типа неравенств. Вычисляются значения f (x ) в найденных точках локального экстремума.
Необходимые условия минимума (максимума) первого порядка. Пусть x −
точка локального минимума (максимума) в задаче (7.11). Тогда найдется такое число λ0 ≥ 0 , и вектор λ = ( λ1 , ..., λm )T , не равные одновременно нулю и такие, что
выполняются следующие условия:
− стационарности обобщенной функции Лагранжа по x
∂L(x , λ0 |
, λ ) |
= 0, i =1, ..., n ; |
∂xi |
|
|
|
|
|
− допустимости решения |
|
|
g j (x ) ≤ 0, j =1, ..., m ;
− неотрицательности для условного минимума
(7.12а)
(7.12б)
λj ≥ 0, j =1, ..., m |
|
(7.12в) |
(условие неположительности для условного максимума λj ≤ 0, |
j =1, ..., m ); |
|
− дополняющей нежесткости |
|
|
λj g j (x ) = 0, j =1, ..., m . |
|
(7.12г) |
Если при этом градиенты активных (т.е. g j (x ) = 0 ) в точке |
x ограничений |
|
линейно независимы (выполняется условие регулярности), то |
λ0 |
≠ 0 . Точки x , |
удовлетворяющие системе (7.12), называются условно-стационарными. Необходимо обратить внимание на следующее.
139
1.В отличие от ограничений типа равенств необходимые условия экстремума первого порядка формулируются отдельно для максимума и минимума. Эти условия впервые были доказаны Куном и Таккером.
2.Если в задаче ограничения записаны в форме g j (x ) ≥ 0, то их необходимо
переписать как − g j (x ) ≤ 0 (7.12).
Обозначим через J a множество индексов ограничений, активных в точке x .
3. При λ0 ≠ 0 необходимые условия минимума (максимума) |
первого порядка |
для выпуклых функций f (x), g j (x), j =1, ..., m ( − f (x), g j (x), |
j =1, ..., m ) будут |
одновременно и достаточными условиями глобального минимума (глобального максимума).
4.Из условия дополняющей нежесткости следует, что если ограничение в точке
xпассивное, т.е. g j (x ) < 0 , то λj = 0 , а если активное, т.е. g j (x ) = 0 , то λj ≥ 0
(для минимума), и λj ≤ 0 (для максимума).
Достаточные условия минимума (максимума) первого порядка. Пусть имеется точка (x , λ ) , удовлетворяющая системе (7.12) при λ0 ≠ 0 , число активных
ограничений в точке x совпадает с числом |
n переменных (при этом условие |
|
регулярности выполняется). Если λj > 0 для всех j J a , то x |
− точка условного |
|
локального минимума. Если λj < 0 для всех |
j J a , то x |
− точка условного |
локального максимума в задаче (7.11).
Необходимые условия минимума (максимума) второго порядка. Пусть x −
точка локального минимума (максимума) в задаче (7.11) и имеется решение (x , λ )
системы (7.12). Тогда второй дифференциал классической функции Лагранжа,
вычисленный в точке (x , λ ) , неотрицателен (неположителен)
d 2 L(x , λ ) ≥ 0 |
|
|
( d 2 L(x , λ ) ≤ 0 ) |
(7.13) |
||
для всех d x таких, что |
|
|
|
|
|
|
d g j (x ) = ∑∂ g j (x |
|
) d xi = 0, j J a , λj > 0 (λj < 0) |
; |
|||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
∂x |
i |
|
|
|
|
i 1 |
|
|
|
|
|
|
d g j (x ) ≤ 0, j J a , λj = 0 .
140

Достаточные условия минимума (максимума) второго порядка. Пусть имеется точка (x , λ ) , удовлетворяющая системе (7.12) при λ0 ≠ 0 . Если в этой точке d 2 L(x , λ ) > 0 ( d 2 L(x , λ ) < 0 ) для всех ненулевых d x таких, что
d g j (x ) = ∑∂ g j (x |
|
) d xi = 0, j J a , λj > 0 (λj < 0) ; |
|||
n |
|
|
|
|
|
|
|
|
|
|
|
= |
∂x |
i |
|
|
|
i 1 |
|
|
|
|
|
d g j (x ) ≤ 0, j J a , λj = 0 ,
то x − точка локального минимума (максимума) в задаче (7.11).
Алгоритм решения задачи.
Шаг 1. Составить обобщенную функцию Лагранжа
λj
λ0
m
L(x, λ0 , λ) = λ0 f (x) + ∑λj g j (x) .
j=1
Шаг 2. Записать необходимые условия минимума (максимума) первого порядка
а) |
∂L(x , λ0 , λ ) |
= 0, i =1, ..., n ; |
б) g j (x |
|
) ≤ 0, j =1, ..., m ; |
∂xi |
|
||||
|
|
|
|
|
в) λj ≥ 0, j =1, ..., m (для минимума), λj ≤ 0, j =1, ..., m (для максимума);
г) λj g j (x ) = 0, j =1, ..., m .
Шаг 3. Решить систему для двух случаев
1)λ0 = 0 ;
2)λ0 ≠ 0 (при этом поделить условия, записанные на шаге 2, на λ0 и заменить
на λj ).
Врезультате найти условно-стационарные точки x , выделив из них полученные при λ0 ≠ 0 (они могут быть регулярными точками экстремума).
Вкаждом из двух случаев следует начинать с рассмотрения 2m вариантов удовлетворения условия "г" дополняющей нежесткости.
Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума первого или второго порядка.
Для проверки достаточных условий первого порядка следует: а) определить число l активных в точке x ограничений;
б) если l = n и λj > 0 для всех j J a , то в точке x − локальный минимум;
141
если l = n и λj < 0 для всех j J a , то в точке x − локальный максимум. Если l < n
или соответствующие множители Лагранжа не удовлетворяют достаточным условиям первого порядка, то проверить достаточные условия второго порядка.
Для проверки достаточных условий второго порядка следует:
а) записать выражение для второго дифференциала классической функции Лагранжа в точке (x , λ )
n n |
2 |
L(x |
|
, λ |
|
) dxi d x j ; |
d 2 L(x , λ ) = ∑∑∂ |
|
|
|
|||
i=1 j=1 |
|
∂xi ∂x j |
|
|
||
б) записать условия, накладываемые на первые дифференциалы активных ограничений
d g j (x ) = ∑∂ g j (x |
|
) d xi |
= 0, j J a ; |
λj > 0 (λj < 0) ; |
(7.14) |
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
∂xi |
|
|
|
|
|
|
|
|
|
|
|
d g j (x ) = ∑∂ g j (x |
|
) d xi ≤ 0, |
j J a ; λj = 0 ; |
|
||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
∂x |
i |
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|||
в) исследовать знак второго дифференциала функции Лагранжа для ненулевых
d x , удовлетворяющих системе |
(7.14). Если d 2 L(x , λ ) > 0 , то |
в |
точке x − |
условный локальный минимум. |
Если d 2 L(x , λ ) < 0 , то в точке |
x |
− условный |
локальный максимум. |
|
|
|
Если достаточные условия первого и второго порядка не выполняются, следует проверить выполнение необходимых условий второго порядка, следуя аналогичной процедуре. Если они выполняются, то требуется дополнительное исследование, а
если нет, то в точке x |
нет условного экстремума. |
|
|
|
|||||
|
|
Шаг 5. Вычислить значения функции в точках условного экстремума. |
|||||||
|
|
Условия экстремума в исходной задаче (7.11) приведены в табл. 7.2. и 7.3. |
|||||||
|
Необходимые и достаточные условия первого порядка в задаче поиска условного |
||||||||
|
|
экстремума при ограничениях типа неравенств |
Таблица 7.2. |
||||||
|
|
|
|
|
|
|
|
||
|
|
Необходимые условия первого порядка |
Достаточные условия первого порядка (λ0 ≠ 0) |
||||||
|
|
|
|
|
|
|
|
||
№ |
x L(x , λ0 , λ ); |
|
g j (x ), |
λ0 ≥ 0, |
Число |
λj , |
Тип условно-стационарной |
||
|
|
λj g j (x ), |
|
j =1, m |
λj , j =1, m |
l |
j J a |
|
точки x |
|
|
j =1, ..., m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
≤0 |
≥0 |
n |
> 0 |
условный локальный минимум |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
≤0 |
≤0 |
n |
<0 |
условный локальный максимум |
|
|
|
|
|
|
|
|
|
|
|
142
Необходимые и достаточные условия второго порядка в задаче поиска условного
|
|
экстремума при ограничениях типа неравенств |
Таблица 7.3. |
|||
|
|
|
|
|
|
|
№ |
d 2 L(x , λ ) |
dg j (x ), |
dg j (x ), |
dg j (x ), |
Тип условно-стационарной точки x |
|
|
|
j J a , |
j J a , |
j J a , |
|
|
|
|
λj > 0 |
λj < 0 |
λj = 0 |
|
|
|
|
|
|
|
|
|
1 |
> 0 |
0, dx ≠ 0 |
− |
≤0 |
условный локальный минимум |
|
|
|
|
|
|
|
|
2 |
<0 |
− |
0, dx ≠ 0 |
≤0 |
условный локальный максимум |
|
|
|
|
|
|
|
|
3 |
≥0 |
0 |
− |
≤0 |
может быть локальный минимум, |
|
|
|
|
|
|
требуется дополнительное исследование |
|
|
|
|
|
|
|
|
4 |
≤ 0 |
− |
0 |
≤0 |
может быть локальный максимум, |
|
|
|
|
|
|
требуется дополнительное исследование |
|
|
|
|
|
|
|
|
5 |
= 0 |
0 |
− |
≤0 |
требуется дополнительное исследование |
|
|
|
|
|
|
|
|
6 |
= 0 |
− |
0 |
≤0 |
требуется дополнительное исследование |
|
|
|
|
|
|
|
|
7 |
> 0, < 0 |
0 |
− |
≤0 |
нет экстремума |
|
|
|
|
|
|
|
|
8 |
> 0, < 0 |
− |
0 |
≤0 |
нет экстремума |
|
|
|
|
|
|
|
|
Пример 7.8. Найти условный экстремум
f (x) = x12 + x22 → extr , g1 (x) = x1 + x2 − 2 ≤ 0 .
□ 1. Составим обобщенную функцию Лагранжа
L(x, λ0 , λ1 ) = λ0 (x12 + x22 ) + λ1 (x1 + x2 − 2) .
2. Выпишем необходимые условия экстремума первого порядка
а) ∂ L(x, λ0 , λ1 ) = 2λ |
x + λ = 0, |
∂ L(x, λ0 , λ1 ) = 2λ |
0 |
x |
2 |
+ λ = 0 |
; |
||
∂x1 |
0 |
1 |
1 |
∂x2 |
|
1 |
|
||
|
|
|
|
|
|
|
|
||
б) x1 + x2 −2 ≤ 0 ; |
|
|
|
|
|
|
|
|
|
в) λ1 ≥ 0 (для минимума), |
λ1 ≤ 0 (для максимума); |
|
|
|
|
|
|||
г) λ1 (x1 + x2 − 2) = 0 . |
|
|
|
|
|
|
|
|
|
3.Решим систему для двух случаев.
Впервом случае λ0 = 0 . Тогда из условия "а" следует, что λ1 = 0 . Это
противоречит требованию существования ненулевого вектора (λ0 , λ1 )T .
143
Во втором |
случае |
λ |
0 |
≠ 0 . |
Поделим систему на λ |
0 |
и |
заменим |
|
λ1 |
на |
λ . |
||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
λ0 |
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обобщенная функция Лагранжа при этом заменяется классической |
|
|
|
|
||||||||||||
а) ∂ L(x, λ1 ) = 2x + λ = 0, |
∂L(x, λ1 ) = 2x |
2 |
+ λ = 0 ; |
|
|
|
|
|
|
|
||||||
|
∂x1 |
|
1 |
1 |
|
|
∂x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) x1 + x2 −2 ≤ 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) λ1 ≥ 0 (для минимума), |
λ1 ≤ 0 (для максимума); |
|
|
|
|
|
|
|||||||||
г) λ1 (x1 + x2 − 2) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Из условия "г" дополняющей нежесткости следует |
|
|
|
|
|
|
|
|||||||||
1) λ1 |
= 0 (фактически решается задача поиска безусловного экстремума). |
|
||||||||||||||
Тогда x = x = 0, |
λ = 0 и условие "б" выполняется. Выполняются необходимые |
|||||||||||||||
1 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
условия и для минимума, и для максимума. |
|
|
|
|
|
|
|
|
|
|||||||
2) λ1 |
≠ 0 . Тогда из системы x1 + x2 −2 = 0 , |
|
2x1 + λ1 = 0 , |
2x2 + λ1 |
= 0 |
|
||||||||||
получаем x = x |
|
=1, λ = −2 . Так как λ < 0 , то необходимое условие минимума не |
||||||||||||||
|
1 |
2 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
выполняется (в точке (1, 1)T нет минимума), но выполняется необходимое условие максимума. Таким образом, имеем две условно-стационарные точки.
4.Проверим выполнение достаточных условий экстремума.
Вточке x = (0, 0)T ограничение не является активным, так как g1 (x) = −2 < 0 ,
поэтому достаточные условия первого порядка не удовлетворяются. Проверим
условия второго порядка. Так как d 2 L(x , λ ) = 2dx2 |
+ 2dx2 |
> 0 при dx ≠ 0 , то в точке |
||
|
1 |
2 |
|
|
x = (0, 0)T |
регулярный локальный условный минимум, |
|
совпадающий в данной |
|
задаче с безусловным. |
|
|
|
|
В точке |
x = (1, 1)T ограничение является активным, |
но l =1 < n = 2 , поэтому |
||
достаточное условие первого порядка не выполняется. Проверим достаточное условие второго порядка.
|
|
|
d 2 L(x , λ ) = 2dx2 + 2dx2 |
, |
|
||||
|
|
|
|
|
|
1 |
2 |
|
|
|
dg |
(x ) = dx + dx |
2 |
= 0 |
откуда dx = −dx . |
||||
|
1 |
|
1 |
|
|
|
1 |
2 |
|
Следовательно, d 2 L(x , λ ) = 4dx22 |
> 0 |
при |
dx2 |
≠ 0 . |
Так как в этой точке |
||||
λ = −2 < 0 |
, то достаточное |
условие максимума |
не |
выполняется. Проверим |
|||||
1 |
|
|
|
|
|
|
|
|
|
достаточное условие максимума второго порядка. Так как d 2 L(x , λ ) = 4dx22 ≥ 0 при
144
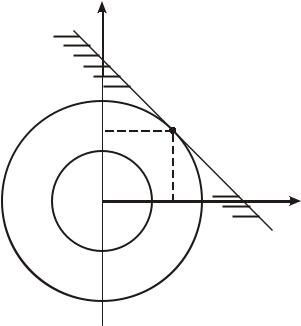
любых dx2 , то необходимое условие максимума не выполняется, поэтому в точке x = (1, 1)T максимума нет.
5. Вычислим значение функции в точке условного минимума f (x ) = 0
(рис.7.7). ■
x2
2
g(x) = x1 + x2 - 2 = 0
1
2 x1
 x* 1
x* 1
Рис.7.7. Иллюстрация к решению задачи из примера 7.8 Пример 7.9. Найти условный экстремум в задаче
f (x) = x1 + x2 →extr ,
g1 (x) = x12 + x22 −1 ≤ 0 .
□ 1. Составим обобщенную функцию Лагранжа
L(x, λ0 , λ1 ) = λ0 (x1 + x2 ) + λ1 (x12 + x22 −1) .
2. Выпишем необходимые условия первого порядка
а) ∂ L(x, λ0 , λ1 ) = λ |
0 |
+ 2λ x = 0 |
, |
∂ L(x, λ0 , λ1 ) = λ |
0 |
+ 2λ x |
2 |
= 0 |
; |
|||
|
∂x1 |
1 |
1 |
|
∂x2 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
б) x2 |
+ x2 |
−1 ≤ 0 ; |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
в) λ1 ≥ 0 (для минимума), |
|
λ1 ≤ 0 (для максимума); |
|
|
|
|||||||
г) λ (x2 + x2 −1) = 0 . |
|
|
|
|
|
|
|
|
|
|||
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
3. Решим задачу для двух случаев.
145
В первом случае λ0 |
= 0 . |
Тогда, согласно необходимым условиям экстремума |
|||||||||
первого порядка требуется, чтобы λ1 ≠ 0 . При этом x1 |
|
= x2 = 0 и не удовлетворяется |
|||||||||
условие "г" дополняющей нежесткости. |
|
|
|
|
|
|
|||||
Во втором случае λ |
0 |
≠ 0 . Поделим уравнения на λ |
0 |
и заменим |
λ1 |
на λ |
|||||
|
|||||||||||
|
|
|
|
|
|
|
|
λ0 |
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
а) ∂ L(x, λ1 ) =1 + 2λ x = 0 |
∂L(x, λ1 ) =1 + 2λ x |
2 |
= 0 ; |
|
|
||||||
|
∂x1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
б) x2 |
+ x2 |
−1 ≤ 0 ; |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
в) λ1 ≥ 0 (для минимума), |
λ1 ≤ 0 (для максимума); |
|
|
||||||||
г) λ (x2 + x2 −1) = 0 . |
|
|
|
|
|
|
|
|
|
||
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
Из условия "г" дополняющей нежесткости следует два варианта
1)λ1 = 0 . Тогда условие "а" не выполняется.
2)λ1 ≠ 0 . Тогда x12 + x22 −1 = 0 и система имеет два решения (рис. 7.8)
точка A : x |
= x = − |
2 , |
λ |
= |
2 |
(в точке A может быть минимум); |
|
|
|||||||||||||
1 |
|
2 |
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точка B : x |
= x = |
|
2 , |
λ = − |
2 |
(в точке B может быть максимум). |
|
|
|||||||||||||
1 |
|
2 |
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Проверим достаточные условия экстремума. |
В точках A и B ограничения |
||||||||||||||||||||
являются активными, |
но |
l =1 < n = 2 . |
Поэтому |
|
условия |
первого |
порядка |
не |
|||||||||||||
выполняются. Проверим условия второго порядка: |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
d 2 L(x , λ ) = 2λ dx2 + 2λ dx2 |
, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
d g |
(x |
) = 2x dx + 2x dx |
2 |
= 0 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
1 |
|
2 |
|
|
|
|
|
|
|
|
В точках |
A и B выполняется dx |
= −dx |
2 |
. Так как d 2 L( A) = 4λ dx 2 |
= 2 2dx 2 |
> 0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
2 |
2 |
|
||
при dx2 ≠ 0 , |
то в точке |
A − регулярный локальный условный минимум. Так как |
|||||||||||||||||||
d 2 L(B) = 4λ dx 2 = −2 |
|
2dx 2 < 0 |
при |
dx |
2 |
≠ 0 , то в точке |
B − регулярный локальный |
||||||||||||||
1 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условный максимум. С другой |
стороны, |
|
функции |
f (x) |
и |
− f (x) = −x1 − x2 |
− |
||||||||||||||
выпуклые и |
ограничение |
выпуклое, |
поэтому в |
точках |
A |
и |
B |
достигается |
|||||||||||||
глобальный экстремум. Достаточные условия первого и второго порядка проверялись для демонстрации методики.
5. Вычислим значение целевой функции в точках условного экстремума: f ( A) = − 2, f (B) =
2, f (B) =  2 . ■
2 . ■
146
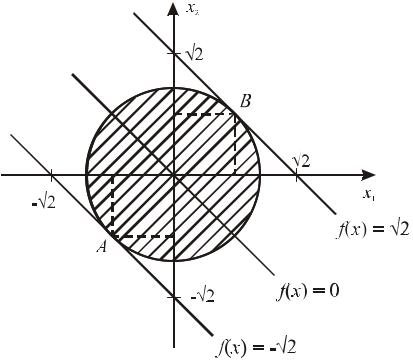
Рис.7.8. Иллюстрация к решению задачи из примера 7.9
Пример 7.10. Найти условный экстремум
f (x) = (x1 − 2)2 + (x2 −3)2 → extr, g1 (x) =x21 +x22 −52 ≤ 0.
□ 1. Составим обобщенную функцию Лагранжа
|
|
L(x, λ |
0 |
, λ ) = λ |
0 |
((x |
− 2)2 + (x |
2 |
−3)2 ) + λ (x2 |
+ x2 |
−52) . |
|
|
|
||||||
|
|
|
|
1 |
1 |
|
1 |
1 |
|
|
2 |
|
|
|
|
|
||||
2. Выпишем необходимые условия первого порядка |
|
|
|
|
|
|
|
|
|
|||||||||||
а) ∂L(x, λ0 , λ1 ) = 2λ |
0 |
(x − 2) + 2λ x = 0 , ∂L(x, λ0 , λ1 ) = 2λ |
0 |
(x |
2 |
−3) + 2λ x |
2 |
= 0 |
; |
|||||||||||
|
∂x1 |
|
1 |
|
1 |
1 |
|
∂x2 |
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) x2 |
+ x2 −52 ≤ 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) λ1 ≥ 0 (для минимума), |
|
λ1 ≤ 0 (для максимума); |
|
|
|
|
|
|
|
|||||||||||
г) λ (x2 |
+ x2 −52) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Решим задачу для двух случаев.
Впервом случае λ0 = 0 . Тогда, согласно необходимым условиям экстремума
первого порядка требуется, чтобы λ1 ≠ 0 . При этом x1 = x2 = 0 и не выполняется условие "г" дополняющей нежесткости.
147
Во втором случае λ |
0 |
≠ 0 . Поделим уравнения на λ |
0 |
и заменим |
λ1 |
на λ |
|||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
λ0 |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) ∂L(x, λ1 ) = 2(x − 2) + 2λ x = 0 |
∂L(x, λ1 ) = 2(x |
2 |
−3) + 2λ x |
2 |
= 0 |
; |
|||||||||||
|
|
∂x1 |
|
1 |
|
|
1 |
1 |
∂x2 |
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) x2 |
+ x2 |
−52 ≤ 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) λ1 ≥ 0 (для минимума), |
λ1 |
≤ 0 (для максимума); |
|
|
|
|
|||||||||||
г) |
λ (x2 + x2 −52) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из условия "г" следуют два варианта |
|
|
|
|
|
|
|
|
|||||||||
1) |
λ1 |
= 0 . |
Тогда |
x1 = 2, x2 |
= 3 и |
выполняются необходимые условия и для |
|||||||||||
минимума, |
и |
для |
|
максимума. |
Имеем условно-стационарную |
точку A : |
|||||||||||
x = 2, x |
= 3, λ = 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) λ1 ≠ 0 . Тогда x12 + x22 −52 = 0 и система имеет решение:
точка B : x |
= 4, x = 6, |
λ = − |
1 |
; точка C : x = −4, x = −6, |
λ = − |
3 |
. |
|
|
|
|||||||
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
||
Так как |
λ1 < 0 в |
обеих |
точках, то в них |
минимума нет, но может быть |
||||
максимум. |
|
|
|
|
|
|
|
|
4. Проверим достаточные условия экстремума. В обеих условно-стационарных точках ограничение превращается в равенство, т.е. активно. Так как число активных ограничений l =1 < 2 = n , то условия первого порядка не выполняются.
Так как функция − f (x) = −(x1 − 2)2 −(x2 −3)2 не является выпуклой, то необходимые условия не являются достаточными. Поэтому проверим условия второго порядка
|
|
|
d 2 L(x , λ ) = (2 + 2λ )dx2 |
+ (2 + 2λ )dx2 . |
|||
|
|
|
1 |
1 |
1 |
1 |
2 |
В точке |
A |
ограничение не |
является |
активным. Так как λ = 0 , то |
|||
|
|
|
|
|
|
|
1 |
d 2 L(x , λ ) = 2dx2 |
+ 2dx2 |
> 0 при dx ≠ 0 |
. Поэтому в точке A − условный локальный |
||||
1 |
1 |
2 |
|
|
|
|
|
минимум. Так как целевая функция выпуклая и множество допустимых значений выпукло, то можно заключить, что в данном случае необходимое условие минимума является достаточным. В точке A − глобальный минимум.
В точках B и C ограничение активно. Поэтому d g |
(x ) = 2x dx |
+ 2x dx |
2 |
= 0 . В |
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
2 |
|
||
точках |
B и |
C выполняется dx |
= − |
3 |
dx |
|
. Так как |
d 2 L(B) = |
(− |
3 |
)dx |
|
2 |
+ dx2 |
> 0 при |
||
|
2 |
|
2 |
|
|||||||||||||
|
|
1 |
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
148
