Одномерная минимизация. Методы, использующие информацию о производных целевой функции

′

≈ 0

или

′

≤ ε может служить условием

[a, b], то приближенное равенство f

(x)

f (x)

остановки вычислений в рассматриваемых трех методах.

3.1. Метод средней точки

Если определение производной

f

′

не

представляет затруднений, то в

(x)

f (x)

вблизи середины очередного отрезка можно заменить вычислением одного

′

a +b

значения f (x) в его средней точке

x =

.

2

В

самом

деле, если f

′

то

точка x лежит на участке монотонного

(x) > 0 ,

возрастания

f (x) , поэтому

x < x ,

и точку минимума следует искать на отрезке

[a, x].

При f

′

(x) < 0 имеем противоположную ситуацию и переходим к отрезку

[x, b]. Равенство

′

означает,

что точка минимума найдена точно

x

= x ,

f (x) = 0

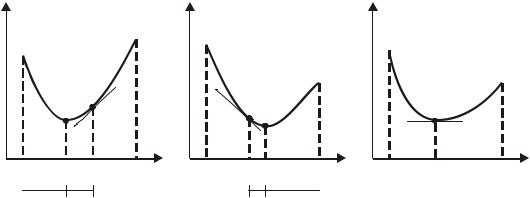
(рис. 3.1).

y

y

y

a

x*

_

b x

a

_

b x

a

_

b x

x

x x*

x*= x

_

_

a

x*

x*

b

x

x

Рис. 3.1. Иллюстрация исключения отрезков методом средней точки

Такое исключение отрезков требует

на каждой

итерации только

одного

′

x

ровно вдвое.

вычисления f (x) и уменьшает отрезок поиска точки

Алгоритм метода средней точки следующий.

Шаг 1. Положить x =

a + b

. Вычислить

f

′

2

(x) . Перейти к шагу 2.

Шаг 2. Проверка на окончание поиска:

если

f

′

≤ ε , то положить

x

= x ,

(x)

f = f (x) и завершить поиск, иначе перейти к шагу 3.

′

′

Шаг 3. Сравнить f (x) с нулем: если f

(x) > 0 , то продолжить поиск на отрезке

x [0, 1], с точностью до

′

(x)

≤ 0,02 .

f

□ Рассмотрим детально действия при выполнении итерации 1.

Шаг 1. Находим x =0,5,

f

′

, переходим к шагу 2.

(x) = −0,107

Шаг 2.

′

> 0,02

, поэтому переходим к шагу 3.

f (x)

Шаг 3.

′

значит

полагаем

a = x = 0,5 , и переходим к следующей

f (x) < 0 ,

Результаты вычислений примера методом средней точки

Таблица 3.1.

′

′

Номер

a

b

x

f (x)

Знак

f (x)

итерации

-0,107

1

0

1

0,5

-

1,215

2

0,5

1

0,75

+

0,441

3

0,5

0,750

0,625

+

0,142

4

0,5

0,625

0,563

+

0,012

5

0,5

0,563

0,531

точность

достигнута

Таким образом, x ≈ 0,531,

f ≈ 0,668 . ■

функции

f (x) получаем n =

b − a

.

2n

Как уже отмечалось, равенство

′

f (x) =0 является необходимым и достаточным

условием

глобального минимума

выпуклой дифференцируемой

функции

f (x) .

Если

на

концах отрезка

[a, b]

производная

′

имеет разные знаки,

т.е.

f (x)

′

′

< 0 , и она непрерывна,

то на интервале (a, b)

найдется точка, в которой

f (a) f (b)

′

обращается в нуль.

В этом случае поиск точки минимума

f (x) на отрезке

f (x)

[a, b]

эквивалентен решению уравнения

′

x (a, b) .

(3.1)

f (x) = 0 ,

Таким

образом, при

′

′

приближенный

метод решения

f (a) f

(b) < 0 любой

Сущность приближенного решения уравнения F(x) = 0 на отрезке [a, b]

при

F(a) F(b) < 0 методом хорд состоит в исключении отрезков путем определения

~

−

x

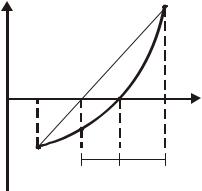
точки пересечения с осью Ox

хорды графика функции F(x) на [a, b] ,

представленного на рис. 3.2.

y

F(x)=f΄(x)

a

~

*

b

x

x

x

~

x*

b

x

Рис. 3.2. Иллюстрация исключения отрезков методом хорд

′

~

Полагая F(x) = f (x) , запишем координату точки x

~

f

′

(3.2)

(a)

− b) .

x = a −

(a

f

′

′

(a) −

f (b)

~

~

Отрезок

дальнейшего

поиска

точки

x

или

в

([a, x]

[x, b] ) выбирается

зависимости

от

знака

′

~

так

же, как

в

методе

средней точки.

На каждой

f (x)

итерации, кроме первой, необходимо вычислять только одно новое значение

′

f

(x) .

Алгоритма метода хорд следующий.

Шаг 1. Найти

~

′ ~

x по формуле (3.2). Вычислить f

(x) и перейти к шагу 2.

Шаг 2. Проверка на окончание поиска:

если

′

~

≤ ε

, то положить

x

= x ,

f (x )

f = f (x)

и завершить поиск, иначе перейти к шагу 3.

Шаг

3.

Переход

к новому

отрезку.

Если

′

~

то положить

~

f (x) > 0 ,

b = x ,

′

′

~

~

, f

′

= f

′

~

f (b) = f (x) , иначе положить a

= x

(a)

(x) . Перейти к шагу 1.

Пример 3.2. Методом хорд решить задачу

f (x) = x4 + e−x →min,

x [0,1] ,

с

точностью до

f

′

≤ 0,05 .

(x)

□ Условие

f

′

′

(0) f (1) < 0 выполняется.

Рассмотрим детально действия при выполнении итерации 1.

~

=0,216,

′

~

= −0,766 . Переходим к шагу 2.

Шаг 1. Находим: x

f (x)

Шаг 2.

f

′

~

> 0,05

, поэтому переходим к шагу 3.

(x )

Шаг

3.

f

′ ~

поэтому

полагаем

a

= 0,216 ,

′

к

(x) < 0 ,

f (a) = −0,766 . Переходим