Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Uch_posobie_po_UR_MAT_FIZ

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.46 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Чтобы удовлетворить нулевым граничным условиям, наложим на функции Φ(x) и Ψ(x)

требования нечетности относительно точек x=0, x=l:

(x) ( x),

Сопоставляя эти равенства, получим:

~ ~ (x ) (x

(x) (2l x),(x) (2l x).

2l)	~	x)
	(x

и аналогично для Ψ(x), то есть Φ и Ψ являются периодическими функциями с периодом 2l.

Нетрудно видеть, что условия нечетности относительно начала координат и условия периодичности определяют продолжение Φ(x) и Ψ(x) на всей прямой x .

Подставляя их, получаем решение задачи.

Пример.	Решить	уравнение								колебания					бесконечной										струны		2u		1 2u		,
Пример.	Решить	уравнение								колебания					бесконечной										струны		t	2	4	x2	,
																											t	2	4	x2
удовлетворяющее условиям:			u(x,0) cosx,
удовлетворяющее условиям:
			ut (x,0) x 1.
Решение: Имеем задачу свободных колебаний бесконечной струны (без краевых
условий). Применяем формулу Даламбера:
					cos(x			1		t) cos(x				1						x	1	t
															t)
																		1			2
																					2
	u(x;t)							2						2						(x 1)dx =
								2						2
											2								1
											2								1		1
																	2		2 x		1	t

																					2
	2cos x cos		t						x		1	t
				(		x2	x)				2
			2			x2					2		cos x cos			t		1	((x				1	t)2	(x	1	t)2 )
													cos x cos						((x					t)2	(x		t)2 )
	2	2							x		1	t		2				2					2			2
									x		2	t
											2

t) (x

t) cos x cos

xt t .

Пример.

Решить

уравнение

колебания

полубесконечной

струны

, 0

x ,

t 0 , удовлетворяющее условиям:

u( x,0) x2 ,ut ( x,0) sin2 x,u(0,t) 0.

Решение: Имеем задачу свободных колебаний полубесконечной струны (с краевым условием u(0,t) 0 ). Так как u(0, t) 0 , то продолжим функции (x) и (x) на отрицательную полуось нечетным образом:

		x	2	,	x 0,

1	(x)
	x2 ,				x 0;

		2		x 0,
1	(x) sin		x,	x 0,
	sin 2 x,			x 0.

Тогда по формуле Даламбера:

x at

u(x,t)

( (x at) (x at))

(s)ds

x at

((x at)2

( x at)2 )

sin2 sds,

x at

((x at)2

( x at)2 )

sin2 sds sin2

sds , 0

x at

a2t2

cos2x sin 2at,

4a (2x sin 2x cos2at),

0 t a .

2axt

t ax ,

Упражнения

Решить уравнение колебания бесконечной струны:

u(x,0) 0,

2.1

t 2

ut (x,0) cos x

Ответ: u(x, t)

cos x sin 5t

u(x,0) cos x,

2.2

ut (x,0) 0

t 2

Ответ: u(x, t) cosx cost

u(x,0) 3cos x

2.3

2sin x

;

t 0

Ответ: u(x, t) 3cosx cost 2sin x sin t

1 2u

u(x,0) x2

2.4

9 x2

t 0

Ответ: u(x, t) x2

2xt

t 2

u(x,0) x,

2.5

;

t 0 1

Ответ: u(x,t) x t

u(x,0) 3sin 2x,

2.6

;

cos 2x

t 0

Ответ: u(x, t) 3sin x cos2t

cos x sin 2t

u(x,0) x2 ,

2.7

;

t 0 sin 3x

Ответ: u(x, t)

(x2 t2 ) 3sin x sin t

u(x,0) cos x,

2.8

;

2sin x

t 0

Ответ: u(x, t) cos x cos2 t

sin x sin 2 t

Решить

уравнение

колебания

полубесконечной

струны

0 x ,

t 0 , удовлетворяющее условиям:

u( x,0) 0,

2.9ut ( x,0) sin x,u (0,t) 0.

Ответ: u(x, t)

2.10

Ответ: u(x, t)

2.11

		sin x sin at						,					at x ,
								,					at x ,
					a
1 cos x cosat
													,		0 x at.
													,		0 x at.
					2
							x2
u( x,0)									,
u( x,0)						1 x2			,
					0,
ut ( x,0)					0,
u (0,t) 0.

	1			(x at)2											(x at)2				at x ,
																	,
	2			(x at)							2				(x at)	2	,
	2		1	(x at)									1		(x at)
		1			(x at)2										(at x)2
		1			(x at)2										(at x)2				0 x at.
																		,
												2					2	,
		2 1			(x at)									1 (at x)
		2 1			(x at)									1 (at x)
u( x,0) 0,
							x2
ut ( x,0)										,
ut ( x,0)							1 x2			,

					0.
u (0,t)					0.

Ответ: u( x, t)	1	ln	1 ( x at)2	.
	4a		1 ( x at)2

sin l , x [0, l],

u(x,0) u(x,0)

(l, ),

0, x

2.12

ut ( x,0) 0,

u(0, t) 0.

Ответ:

0 t

sin x cos at ,

0 x l at,

u( x, t)

( x at)

sin

l at x l at,

l at x .

0 x at l,

u( x, t)

sin

( x at)

at l x at l,

l at x .

2.3Метод Фурье (метод стоячих волн). Метод разделения переменных

Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение волнового уравнения с начальными и граничными условиями:

	2u		a2	2u		( l x l,	t 0),
	t	2		x	2

u( x,0) (x),

ut (x,0) (x),u(0, t) 0,

u(l, t) 0.

Уравнение линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение. Частные решения будем искать в виде:

u(x,t) X (x) T (t),

где X (x) – функция только переменного x, T (t) – функция только переменного t.

Подставляя предполагаемую форму решения в уравнение, получим:

X (x) T (t) a12 T (t) X (x)

или, после деления на X (x) T (t) ,

	1
X (x)		T (t)	.

X (x)	a2 T (t)

Правая часть полученного равенства является функцией только переменного t, а левая

– только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим,

что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение


X (x)	1 T (t)	,

X (x)	a2 T (t)
X (x)	a2 T (t)

где – постоянная, которую для удобства последующих выкладок берем со знаком минус,

ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t) :

X X 0,
T a2 T 0.
Очевидно, что нас интересуют нетривиальные решения ( X (x) 0,	T (t) 0 ).
Граничные условия дают:
u(0, t) X (0) T (t) 0,
u(l, t) X (l) T (t) 0.
Отсюда следует
X (0) X (l) 0 .

Таким образом, мы приходим к простейшей задаче: найти те значения параметра ,

при которых существуют нетривиальные решения задач:

T a2T 0,

X X 0,

X (0) X (l) 0.

а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи. Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.

Рассмотрим отдельно случаи, когда параметр отрицателен, равен нулю или положителен.

1. При 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения X X 0 имеет вид

X (x) C1e x C2e x

Граничные условия дают:

X (0) C1 C2 0 ,

X (l) C1el C2e l .

Отсюда C1 C2 0 и, следовательно, X (x) 0 .

2. При 0 также не существует нетривиальных решений. Действительно, в

этом случае общее решение уравнения (15) имеет вид

X (x) C1 x C2 .

Граничные условия дают:

X (0) C2 0 ,

X (l) C1l 0 .

Отсюда C1 C2 0 и, следовательно, X (x) 0 .

3.При 0 общее решение уравнения может быть записано в виде

X (x) C1 cos(x ) C2 sin(x ) .

Граничные условия дают:

X (0) C1

X (l) C2 sin(l

) 0.

Нетривиальное решение получаем только в случае sin

l 0 или

l n,

n Ζ . Отсюда

Этим собственным значениям соответствуют собственные функции

(x) C

sin nx ,

где Cn – произвольная постоянная. Пусть Cn 1.

Аналогично решаем уравнение относительно T (t) :

T (t) A cos nat B sin nat

где An и Bn – произвольные постоянные.

Следовательно, функции

u		(x, t) X				nat	B sin	nat	nx
u		(x, t) X		(x)T (t) A cos			B sin	sin
	n		n	n	n	l	n	l	l

являются частными решениями данного уравнения. В силу линейности и однородности уравнения сумма частных решений также удовлетворяет этому уравнению и граничным условиям. Получаем общее решение:

				nat		Bn			nat
u(x, t) un (x, t)		An cos		l		Bn		sin	l	sin
n 1	n 1			l					l
Начальные условия позволяют определить An		и Bn :
							nx ,
	u(x,0) (x) An sin						nx ,
		n 1					l
			na					nx .
	ut (x,0) (x)		na		Bn		sin	nx .
		n 1		l				l

nx l

Из теории рядов Фурье известно, что коэффициенты разложения в ряд Фурье

вычисляются по формулам:

2 l

(x) sin

dx ,

(x)sin nx dx .

Подставив эти коэффициенты в общее решение, мы удовлетворим краевым условиям

и получим решение уравнения.

Простейшие задачи Штурма-Лиувилля для уравнения X X 0 :

Вид условия

Собственные значения и функции

X (0) X (l) 0

sin

n 1,2,...

X n (x)

X (0) X (l) 0

(2n 1)

(2n 1)x

X n (x) cos

n 1,2,...

X (0) X (l) 0

(2n 1)

(2n 1)x

X n (x) sin

n 1,2,...

X (0) X (l) 0

cos

n 1,2,...

X n (x)

Пример. Решить

уравнение

колебания ограниченной струны

3 x

u(x,0)

sin

удовлетворяющее условиям:

ut (x,0) 0,

u(l, t) 0.

u(0, t)

Решение: Общее решение имеет вид:

			nat			nat		nx
u(x, t)				Bn
	An	cos			sin		sin

n 1			l			l		l

Из начальных условий определим An и Bn :

			sin nx		1		3 x
		u( x,0) An			1	sin	3 x	,
		u( x,0) An			8	sin	l	,
		n 1		l	8		l
тогда A	1	(n 3) .
тогда A		(n 3) .
3	8
	8
			na		nx
		ut ( x,0)	na	Bn sin	nx		0,
		n 1	l			l

отсюда Bn 0 .

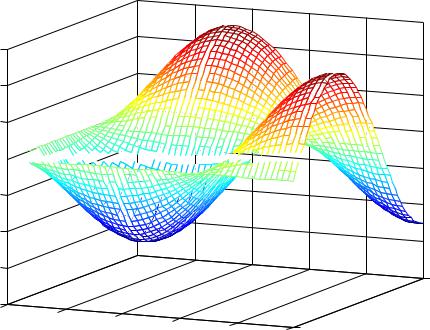
Подставив эти коэффициенты в общее решение, получим решение уравнения: u(x, t) 81 cos 3l t sin 3l x

Можно построить в среде MATLAB поверхность u u(x, t) решения данного волнового уравнения. Для этого напишем m-файл:

[x,t]=meshgrid(0:.1:5); u=1/8*sin(3*pi*x/10).*cos(3*pi*t/10); mesh(x,t,u)

xlabel('x') ylabel('t') zlabel('u(x,t)')

title('Поверхность решения волнового уравнения')

u(x,t)

Поверхность решения волнового уравнения

0.15

0.1

0.05

-0.05

-0.1

-0.15

-0.2
5	4	3
	4		2
				1		0
					0
					0

t	x

Рис. 7. Поверхность решения волнового уравнения

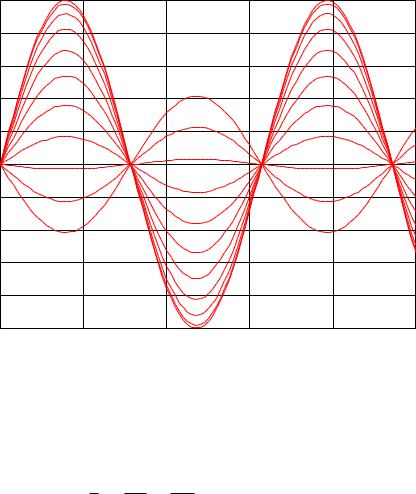
Для лучшей визуализации напишем m-файл, который будет с частотой в 1 секунду демонстрировать графики решения волнового уравнения u(x, t) cost sin x для различных моментов времени t:

figure,axis([0 10 -1 1]),grid hold on

x=0:.1:10;

t=0:.2:2;

for k=1:length(t) u=sin(x)*cos(t(k)); plot(x,u,'r') xlabel('x') ylabel('u')

title('Колебание струны u(x,t)=sin(x)cos(t)') pause(1)

end

			Колебание струны u(x,t)=sin(x)cos(t)
	1
	0.8
	0.6
	0.4
	0.2
u	0
	0
	-0.2
	-0.4
	-0.6
	-0.8
	-10	2	4	6	8	10
				x
Рис. 8. График профиля колебания струны u u( x)					для различных моментов времени t
Для создания анимации в среде MATLAB можно написать m-файл решения волнового

уравнения, например, u(x, t) 81 cos 3l t sin 3l x :

x=0:.1:10; for t=0:20;

u=1/8*sin(3*pi*x/10).*cos(3*pi*t/10); plot(x,u,'r');

hold all; xlim([0 10]); ylim([-1/8 1/8]); grid on; xlabel('x') ylabel('u')

title('Колебание струны') M(t+1)=getframe

pause(.5) hold off;

end

movie(M,5)%повторяем 5 раз

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.11.2019458.24 Кб6topograficheskie_znaki (1).doc
#
26.11.201981.41 Кб6Trite metaphors.doc
#
25.11.20195.02 Mб93Uchebno-metodicheskoe_posobie_po_kursu_laborato...doc
#
01.04.20254.18 Mб2Uchet_i_analiz_1.doc
#
01.04.2025579.07 Кб0uch_metodicheskoe_posobie_vsyo.doc
#
05.06.20151.46 Mб35Uch_posobie_po_UR_MAT_FIZ.pdf
#
14.11.2019866.3 Кб3UMK_strakhovanie_080102_080105_080109__Stepan.doc
#
05.06.201512.36 Кб14Unit 22.docx
#
05.06.20151.27 Mб12Untitled_1 (1).pdf
#
01.04.20253.25 Mб2Uslovnye_topograficheskie_znaki.docx
#
05.06.201513.95 Кб327Ustav_vnutrenney_sluzhby.docx