Uch_posobie_po_UR_MAT_FIZ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Можно подобрать коэффициенты An так,

чтобы равенство выполнялось

при n 3, следовательно,

A 0, n 3 .

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Пример. Решить уравнение колебания ограниченной струны:

					u(x,0)				1	sin	3 x
					u(x,0)					sin
2u								4				2
			2u					4				2
		9				u

t	2		x	2				sin x
	2			2	t			sin x
							t 0

								u(2,t)				0

					u(0,t)

Решение: Имеет место задача свободных колебаний струны, закрепленной на концах

(в точках 0 и 2). Здесь a2 9 , т.е. a 3, l 2 . Поэтому решение имеет вид:

3 n

nx .

u(x;t) ( An cos

Bn sin

t)sin

n 1

Подставим t=0:

u(x;0) ( An cos0 Bn sin 0)sin nx

An sin

nx ,

n 1

Используя первое начальное условие, получаем:

3 x

An sin

sin

n 1

Чтобы использовать второе начальное условие, продифференцируем u(x;t) по

3 n

(

An sin

Bn cos

t)sin

n 1

и подставим t=0:

3 n

(

An sin 0

Bn cos0)sin

Bn sin

t 0

n 1

Таким образом, получаем условие

3 n

Bn sin nx sin x

n 1

и подбираем коэффициенты:

тождественно:

nx .

nx x	при n 2;	3 2	B	1	B	1	;	B 0, n 2 .

2		2	2		2	3		n

Итак, имеется всего два ненулевых слагаемых: при n=2 ( B2 31 ) и при n=3 ( A3 14 ).

Окончательно, получаем решение:

u(x;t) B2 sin 3 2 2 t sin 22x A3 cos 3 2 3 t sin 23x

31 sin 3 t sin x 14 cos 92 t sin 32x .

Замечание. Часто начальная скорость точек струны (х)=0 (то есть рассматриваются колебания струны, которую в начальный момент времени оттянули и отпустили без рывка),

тогда, очевидно, Вn=0.

Пример. Решить уравнение колебания ограниченной струны:

		u(x,0) x(3 x)
2u	2u		u

				0

t2	x2		t
				t 0
				t 0
		u(0,t) u(3,t) 0

Решение: Имеем задачу свободных колебаний струны, закрепленной на концах, где a 1 , l 3. Решение имеет вид:


														u(x;t) ( An cos n t Bn sin n t)sin nx
																	n 1										3									3							3
																	n 1
Используем первое начальное условие:
																												nx
															u( x,0) An sin													nx				x(3 x) .
																			n 1											3
Подобрать коэффициенты An																	здесь нельзя, будем их вычислять как коэффициенты
Фурье разложения функции x(3 x)																	на интервале (0;3) по синусам:
									2		3						nx									u 3x x2													du (3 2x)dx
									2								nx
				An								x(3			x)sin							dx																						3					nx
				An								x(3			x)sin							dx																						3					nx
									3 0									3								dv sin							nx dx				v									cos
									3 0									3								dv sin							nx dx				v						n			cos			3
																																		3									n						3
												2			3	x(3 x)cos nx													3		3			3								nx dx)
																													3					3
													(																					(3 2x)cos
													(																		n			(3 2x)cos
											3				n									3					0		n			0										3
																													0					0
															u 3 2x												du 2dx
																			nx																nx
																			nx												3				nx
															dv cos									dx			dv							sin
															dv cos									dx			dv				n			sin
																					3										n					3
																			3																				3								3
																			3																				3								3
	2		(			3			x(3 x)cos nx															3		(	3			(3 2x)sin						nx					2				3		sin nx dx))
			(		n				x(3 x)cos nx																	(	n			(3 2x)sin											2			n			sin nx dx))
3					n										3				0				n				n									3			0					n			0			3
																			0																				0								0
		2		(		3				x(3 x)cos nx										3				9						(3 2x)sin						nx				3					54			cos nx			3 )
		2				3																		9												nx				3					54
																									n 2																	n 3
3							n										3			0																		3		0										3	0
3							n										3			0																		3		0										3	0
									36					cos n cos0													36				( 1)n 1										36				1		( 1)n .

								n 3																			n 3											n 3
																																																		28

Второе начальное условие тривиально, поэтому Bn=0.

Таким образом, получаем ответ:

	36	1 ( 1)n cos	n t sin	nx .
u(x;t)
	n 3
n 1			3	3

Упражнения

Решить уравнение колебания ограниченной струны:

										u(x,0)				3	sin	2 x
										u(x,0)					sin
	2u												7		3
							2u						7		3
2.13					25						u				;
2.13															;
	t		2				x		2				0
			2						2	t			0
												t 0

													u(3,t) 0

										u(0,t)

Ответ: u(x, t)		3		cos		nt		sin		nx .
Ответ: u(x, t)				cos				sin		nx .
		7				3				3

						u(x,0)				2	sin x
						u(x,0)					sin x
											2
		2u		2u							2
2.14	4						u
2.14
		t	2	x	2				0
			2		2	t			0
								t 0

									u(2,t) 0

						u(0,t)

Ответ:

u(x,0) 0,

2.15

sin 2 x

;

t 0

9 x2

x 0

x 3

Ответ:

u(x,0) sin

2.16

;

; u

sin x

t 0

x 6 0

x 0

Ответ:

u(x,0) x(3 x)

2.17

;

t 0

u(0,t) u(3,t) 0

Ответ:

;

2.182ut2

Ответ:

2.192ut2

Ответ:

u(x,0) 2

2 x

;

t 0

x 0

x 4

		u(x,0) 0,
	2		u
25	u						x(x 5)
	u
		;			t 0
	x2	;	t
	x2		t
		u		x 0		u		x 5	0
				x 0				x 5

Глава 3. Уравнение теплопроводности. Решение уравнения

теплопроводности методом Фурье

3.1Вывод уравнения теплопроводности

Рассмотрим однородный теплоизолированный с боков стержень конечной длины l

имеющий постоянную по длине толщину, и настолько тонкий, чтобы в любой момент времени температуру тела во всех точках поперечного сечения можно было бы считать

одинаковой.

Выберем ось х (направив ее по оси стержня) так, чтобы стержень совпадал с отрезком

[0, l] оси х.

Обозначим температуру стержня в сечении х в момент времени t через u(x, t) . Тогда

функция u u(x, t) дает закон	распределения температуры в	стержне.	Выведем
дифференциальное уравнение для этой функции.
Выделим элемент стержня	[x, x x] и составим для него	уравнение	теплового

баланса, согласно которому скорость изменения количества тепла в рассматриваемом объеме, обусловленная теплоѐмкосью материала, равна количеству тепла, поступившему в этот объем в единицу времени вследствие теплопроводности. Скорость изменения тепла в

	x x		c s u(x, t) dx , где c – теплоемкость материала
выделенном элементе стержня равна			c s u(x, t) dx , где c – теплоемкость материала
		x	t
		x
стержня, – плотность материала,		s	– площадь поперечного сечения. По теореме о
среднем:
x x	c s u(x, t) dx c s ut (x1 , t) x,
	c s u(x, t) dx c s ut (x1 , t) x,			x1 (x, x x) .
x	t
x

Теперь найдем количество тепла, поступившее в выделенный элемент стержня за единицу времени. Так как стержень теплоизолирован с боков, то тепло может поступать только через сечения, ограничивающие выделенный элемент стержня. Поэтому искомое количество тепла с учетом формулы Лагранжа равно:

					(x2	, t) x,		x2 (x, x x) ,
ks(ux	( x x, t) ux ( x, t))			ksuxx	(x2	, t) x,		x2 (x, x x) ,
где k - коэффициент теплопроводности.
Составим уравнение теплового баланса
		( x1	, t) x k s				( x2	, t) x .
	c s ut	( x1	, t) x k s			uxx	( x2	, t) x .

Разделим обе части этого уравнения на s x (объем выделенного элемента стержня) и

устремим x 0 (тогда x1 , x2 x ). Получим

u		2u
						k
	a2			,	a		.

t		x	2			c

Это уравнение называется уравнением теплопроводности для однородного стержня.

Величина a	k	называется коэффициентом температуропроводности.

	c

3.2Метод Фурье для конечного стержня

Уравнение теплопроводности относится к уравнениям параболического типа.

Будем искать решение уравнения теплопроводности с начальными и граничными условиями:

	u a2		2		u2 , (0 x l,
			2
						t 0),
	t	x
	u( x,0)			( x),

u(0, t) 0,
		0.
u(l, t)		0.

Частные решения данного уравнения будем искать в виде:

u(x,t) X (x) T (t),

где X (x) – функция только переменного x, T (t) – функция только переменного t.

Подставляя предполагаемую форму решения в уравнение, получим:

X (x) T (t) a12 T (t) X (x)

или, после деления на X (x) T (t) ,

	1
X ( x)		T (t)	.

X (x)	a2 T (t)

Правая часть полученного равенства является функцией только переменного t, а левая

– только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим,

что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение

где – постоянная, которую для удобства последующих выкладок берем со знаком минус,

ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t) :

X X 0,

T a2 T 0.

Очевидно, что нас интересуют нетривиальные решения ( X (x) 0,

T (t) 0 ).

Граничные условия дают:

u(0, t) X (0) T (t) 0, u(l, t) X (l) T (t) 0.

Отсюда следует

X (0) X (l) 0 .

Таким образом, мы приходим к простейшей задаче: найти те значения параметра ,

при которых существуют нетривиальные решения задач:

T a2T 0,

X X 0,

X (0) X (l) 0.

а также найти эти решения.

При решении уравнения колебания струны было доказано, что при 0					и 0
уравнение X X 0	имеет только тривиальные решения,			поэтому рассмотрим только
случай 0 . Тогда	решение уравнения X X 0 с			учетом граничных	условий
X (0) X (l) 0 имеет вид:
	X	n	( x) sin nx ,
		n	l
			l

а решение уравнения T a2 T 0 имеет вид:

Tn (t) Cn e a2t ,

где Cn – неопределенный пока коэффициент.

Тогда частные решения уравнения теплопроводности

un (x, t) X n (x) Tn (t) Cn e a2t sin nxl ,

А общее решение

u(x, t) Cn e a

t sin

na 2

sin nx .

nx Cn e l

n 1

Начальные условия позволяют определить Cn :

u( x,0) ( x) Cn

sin

n 1

Для выполнения этого начального условия необходимо взять в качестве Cn

коэффициент Фурье:

2 l

(x) sin

dx .

Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.

u(0, t)

где Cn

Пример. Найти решение уравнения теплопроводности при граничных условиях

u(l, t) 0

0 x l / 2,

и начальном условии u(x,0)

l x,

l / 2 x l.

Решение. Общее решение уравнения имеет вид:

u( x, t) Cn e

sin

n 1

l / 2

nx dx

nx dx .

x sin

(l x) sin

l / 2

Вычисляя данный интеграл, получим

l / 2

l 2

x sin

cos

sin

2 n

l 2

(l x) sin

cos

sin

2 n

l /1

sin n .

2n2

Так как sin n 0

, то C

0, C

4l ( 1)n 1

2n 1

2 (2n 1)2

Итак,

u(x, t) 4l2

( 1)n 1

(2n 1)a 2

sin (2n 1)x .

2 e

n 1

(2n 1)

Упражнения:

Решить уравнение теплопроводности:

3.1ut

Ответ:

3.2ut

Ответ:

3.3 t

Ответ:

3.4 t

Ответ:

3.5 t

Ответ:

u(x,0)

sin x

;

u(0,t) u(2,t) 0

1 2u

2sin

5 x

u(x,0)

;

9 x2

u(0,t) u(6,t) 0

x, [0,

u(x,0)

x, (1,

2] ;

4 x2 ;

x 2 0

x 0

u(x,0) x(4 x)

x 4 0

x 0

x / 4, [0,

u(x,0)

;

, (4,

x 0

x 4

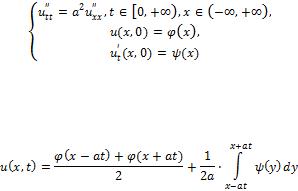
Приложения

Практикум в среде MATLAB

Волновые уравнения

Аналитические методы решения волновых уравнений. Метод Даламбера. Создание анимации средствами MATLAB.

В этой работе мы переходим к изучению методов решения уравнений в частных производных. В работе рассмотрим задачу Коши для уравнения колебаний струны

(волнового уравнения).

Нашей целью будет познакомиться с аналитическими методами решения данной задачи и провести расчеты с помощью MATLAB.

1.Задача Коши для неограниченной струны.

Рассмотрим одномерную бесконечную струну. Пусть в начальный момент времени струну отклонили от равновесного положения (придали некоторую начальную форму) и/или приложили некоторый распределенный импульс к точкам струны.

Последующие колебания струны описываются следующей системой уравнений,

получившей название задача Коши:

Известно, что решение данной задачи можно найти с помощью формулы Даламбера:

Для упрощения вычислений по данной формуле воспользуемся средствами MATLAB.

Пример 1.

Задание: Дана задача Коши для неограниченной струны:

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.09.2019107.52 Кб12test1.doc
#
05.06.20151.22 Mб103Testy_k_ekzamenu.doc
#
16.11.2019458.24 Кб3topograficheskie_znaki (1).doc
#
26.11.201981.41 Кб3Trite metaphors.doc
#
25.11.20195.02 Mб59Uchebno-metodicheskoe_posobie_po_kursu_laborato...doc
#
05.06.20151.46 Mб26Uch_posobie_po_UR_MAT_FIZ.pdf
#
14.11.2019866.3 Кб2UMK_strakhovanie_080102_080105_080109__Stepan.doc
#
05.06.201512.36 Кб12Unit 22.docx
#
05.06.20151.27 Mб8Untitled_1 (1).pdf
#
05.06.201513.95 Кб318Ustav_vnutrenney_sluzhby.docx
#
05.06.20153.73 Mб43VAMS-LRM-2-3-1.pdf