Uch_posobie_po_UR_MAT_FIZ

Найти решение задачи при x = 4 в момент времени t = 2.

Решение:

1. Сначала создаем две вспомогательные функции-файла для вычисления начального отклонения и начальной скорости.

Функция для начального отклонения будет иметь вид: function u = u0(x)

u(abs(x) <= 2) = 1; u(abs(x) > 2) = 0;

end

Функция для начальной скорости будет иметь вид: function u = u_t0(x)

u(abs(x) <= 2) = 2-x; u(abs(x) > 2) = 0;

end

Обратите внимание, что мы используем при заполнении переменной u операции логического индексирования. Такой вид записи позволяет нашим функциям работать правильно в том случае, если х будет являться не числом, а массивом чисел. Данное свойство нам понадобится в дальнейшем при вычислении интеграла от начальной скорости (второе слагаемое в формуле Даламбера).

2.Сохраняем написанные функции в файлы с именами u0.m и u_t0.m, соответственно.

3.Выполняем расчет по формуле Даламбера:

>>x = 4;

>>t = 2;

>>a = 2;

>>u = (u0(x- a*t) + u0(x + a*t)) / 2 + quad(@u_t0, x - a*t, x + a*t)

37

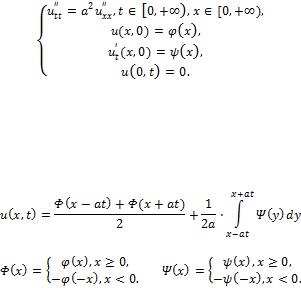
Обратите внимание, что мы воспользовались встроенной функцией численного вычисления интеграла (quad), которая дает приближенное значение интеграла. Для повышения точности можно вычислять интеграл аналитически с помощью символьных функций, либо вычислить его точный вид предварительно на бумаге.

Упражнение 1.

1)На основе примера 1 написать скрипт, позволяющий вычислять значения функции на отрезке по x (для некоторого массива значений переменной x) в заданный момент времени t.

2)С помощью написанного скрипта решить задачу Коши из примера 1 для произвольных x и моментов времени t = 1, 2, 5, 10.

3)Построить графики, отображающие полученные решения.

Замечание: При выборе отрезка по x необходимо задавать его границы так, чтобы на данном отрезке было представлена вся ненулевая часть решения в заданный момент времени.

2. Задача Коши для полуограниченной струны. Метод продолжений.

Теперь рассмотрим полуограниченную струну закрепленную на одном конце.

Возможны два основных способа закрепления струны: жесткое и свободное закрепление.

В случае жесткого закрепления на конце струны ставят дополнительное условие В результате рассматривают задачу Дирихле вида:

Для решения данной задачи используют метод продолжений, заключающийся в том,

что функции и продолжают в отрицательную область нечетным образом. В итоге получаем модифицированную формулу Даламбера:

38

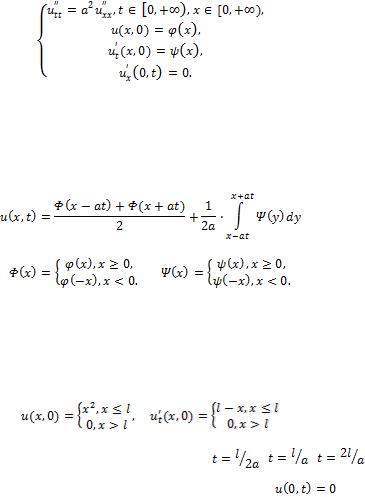
Теперь рассмотрим так называемое свободное закрепление. В этом случае дополнительное условие на границе ставится таким образом, чтобы конец струны оставался всегда параллелен оси x. Таким образом приходим к задаче Неймана для струны:

Для решения данной задачи используют метод продолжений, заключающийся в том,

что функци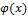и и 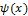продолжают в отрицательную область четным образом. В итоге получаем модифицированную формулу Даламбера:

Упражнение 2.

В области 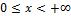, 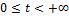найти решение уравнения колебания струны (,

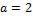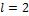), удовлетворяющее условиям

закрепление струны.

Интервал отображения по оси x выбрать равным [0, 2l].

3.Создание анимации средствами MATLAB.

При решении уравнений в частных производных регулярно возникает необходимость отобразить развитие функции решения в зависимости от времени. В предыдущих упражнениях мы отображали полученные решения для нескольких моментов времени.

Но очень часто возникает ситуация, когда моментов времени которые нас интересуют достаточно много. В этом случае, приходится строить большое количество графиков, анализ которых становится слишком трудоемким.

MATLAB позволяет ускорить данный анализ с помощью средств анимации графики.

Общая идея, которая лежит в основе создания анимации в MATLAB, заключается в следующем. Выбирается некоторое равномерное разбиение интервала по времени

39

(некоторый шаг). Для последовательных моментов времени, отстоящих на данный шаг,

строится отдельный график. Таким образом, получается последовательность графиков,

которая впоследствии превратится в последовательность кадров для создаваемой анимации.

Созданная последовательность кадров сохраняется в массив с помощью специальной команды getframe. Вызов данной функции осуществляется для каждого кадра (графика).

Возможно поместить рисование кадров в цикл с перерисовкой одного графического окна в каждом цикле. При этом команда getframe должна быть вызвана на каждой итерации цикла.

Сохраненная последовательность кадров может быть проиграна с помощью команды movie. Первым параметром данной команды является массив сохраненных кадров, вторым необязательным параметром число повторений последовательности при проигрывании.

Существует возможность сохранить записанную анимацию в файл с помощью команды movie2avi.

Пример 2.

Задание:

Задано уравнение функции от координаты x и от времени .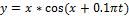

Отобразить данную функцию для моментов времени от 0 до 100 с шагом 1. Сохранить последовательность графиков в виде анимации.

Дополнительно на графике отобразить асимптоты графика y = x и y = -x.

Решение:

x=-4*pi:pi/20:4*pi;

for t=0:100

y=x.*cos(x+pi*t/10.0);

plot(x,y,'b-');

hold all;

plot(x,x,'r-');

plot(x,-x,'r-');

xlim([-4*pi 4*pi]);

ylim([-4*pi 4*pi]);

grid on;

xlabel('x');

40

ylabel('y');

M(t+1)=getframe;

hold off;

end

movie(M, 20) % повторяем 20 раз

Упражнение 3.

Для задач, рассмотренных в упражнении 2, построить анимированный график зависимости колебаний струны от времени. Конечное время и шаг по времени выбрать из условия отсутствия резких скачков между кадрами и полного затухания колебаний в конечный момент времени.

4.Фазовая плоскость. Бегущие волны.

Вупражнениях 1 и 2 мы получали решения заданных уравнений, используя подстановку значений в готовую формулу. При этом область решения определялась автоматически по полученному графику. В этом разделе мы рассмотрим детально поведение решения, рассмотренных в упражнениях 1 и 2 задач.

При аналитическом решении задачи (на бумаге) предварительно всегда проводят анализ будущего решения, выявляя подобласти с определенными его свойствами. Для выявления характера решения задачи удобно воспользоваться плоскостью состояний (x, t)

или фазовой плоскостью.

Пусть начальное отклонение струны и/или начальный импульс локализованы в области 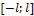. Проведем через концы отрезка локализации прямые 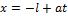, , , 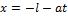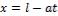(такие прямые обычно называют характеристиками). Получим картину аналогичную, представленной на рисунке 1.

Полуплоскость 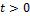разбивается на 6 областей. Рассмотрим поведение решения в каждой из них отдельно.

41

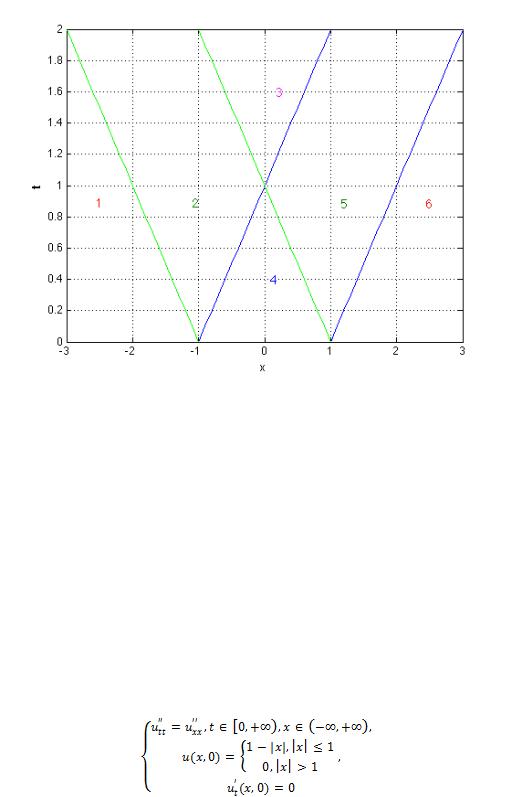
Рисунок 1. Фазовая плоскость для случая .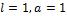

Сначала рассматриваем случай нулевой начальной скорости 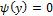. Решение задачи будет представлять из себя комбинацию двух «бегущих волн», каждая из которых описывается функцией 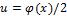. Первая волна будет «бежать» влево и ее границы будут всегда совпадать с «зелеными» характеристиками, вторая волна будет «бежать» вправо и ее границу будут совпадать с «синими» характеристиками.

В областях 1, 3 и 6 в этом случае колебаний не будет; в области 2 будет только левая волна; в области 5 только правая; в области 4 колебания будут являться суммой двух волн.

Пример 3.

Пусть дана задача Коши для неограниченной струны:

Фазовая плоскость для этой задачи, совпадает с фазовой плоскостью на рисунке.

Построим графики решения задачи для моментов времени t = 0; t = 0.5; t = 1 и t = 1.5

воспользовавшись представлением решения в виде комбинации двух бегущих волн.

Текст функции для построения данных графиков будет иметь вид:

a=1;

42

ylim([0 2]); grid on; xlabel('x'); ylabel('u');

title(['t=' num2str(t)]); end

В результате выполнения скрипта получаем результат, представленный на следующем рисунке.

43

Теперь рассмотрим случай нулевого начального отклонения 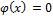. В этом случае,

характерные области сохраняются те же, но форма решения будет описываться более

сложным образом.

Вобластях 1 и 6, как и в первом случае, колебаний не будет.

Вобласти 2 будет наблюдаться бегущая влево волна, форма которой в нулевой момент времени описывается уравнением

Вобласти 5 будет наблюдаться бегущая вправо волна, форма которой в нулевой момент времени описывается уравнением

Вобласти 3 решение будет задано константой равной значению интеграла

Значение интеграла в области 3 совпадает со значениями на границе областей 2 и 5. В

области 4 форма решения наиболее сложная. В зависимости от x она описывается уравнением:

44

К сожалению, для областей 3 и 4 интерпретация решения в виде комбинации волн из решения для областей 2 и 5 невозможна.

В общем случае, когда и начальное отклонение и начальная скорость не равны 0,

решение описывают как комбинацию двух решений. Первое – это комбинация двух бегущих волн, созданных начальным отклонением, второе – это решение, зависящее только от начальной скорости.

Упражнение 4.

Дана задача Коши для неограниченной струны:

1.Построить фазовую плоскость для данной задачи.

2.Построить графики решения для моментов времени , , 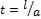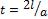. Для

построения воспользоваться построенной фазовой плоскостью и представлением в виде

бегущих волн для характерных областей.

45

Индивидуальные задания

Вариант 1

1.Полуограниченная струна ( u(0, t) 0 , a 3, l 5 ) в начальный момент имеет форму

Найти форму струны и построить графики решения для моментов времени t l / 4a; t l / a; t 3l / 2a; t 7l / 4a .

46