
Uch_posobie_po_UR_MAT_FIZ
.pdf
Глава 1. Дифференциальные уравнения в частных производных.
Задача Коши. Типы уравнений второго порядка в частных производных.
1.1Дифференциальные уравнения в частных производных.
Рассмотрим функцию нескольких независимых переменных u u(x1 , x2 ,..., xn ) .
Частные производные 1-го порядка данной функции по переменной xk вычисляются по обычным правилам и формулам дифференцирования, при этом все переменные, кроме xk ,
рассматриваются как постоянные.
|
|
, |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Обозначение: u x |
xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частными производными 2–ого порядка функции |
|
u u(x1 , x2 ,..., xn ) |
называются |
||||||||||||||||||||||
частные производные от ее частных производных первого порядка. |
|
|
|
|||||||||||||||||||||||
|
|
, |
|
2u |
, |
|
|
2u |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Обозначение: ux x |
ux x , |
x2 |
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
k |
k |
|
k l |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример. Найти |
частные |
|
производные |
1-го |
и |
2-го |
порядков |
функции |
|||||||||||||||||
u x3 5xy 2 3y 25 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
2 |
5 y |
2 |
|
|
|
|
|
|
|
|||
|
Считая y постоянной, получим: |
|
|
ux |
|
|
. |
Считая |
x |
постоянной, |
получим: |
|||||||||||||||
|
10 xy 3 . Соответственно: |
|
|
6x , |
|
|
10 y , |
|
10 x . |
|
|
|
||||||||||||||
u y |
u xx |
uxy |
u yy |
|
|
|
||||||||||||||||||||
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным. Если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:
1.x 2 y 3xy x3 0 – обыкновенное дифференциальное уравнение 1-го порядка;
2.d 2 y 3 dy x – обыкновенное дифференциальное уравнение 2-го порядка; dx2 dx
3.xy x 2 y 5y – обыкновенное дифференциальное уравнение 3-го порядка;
1

4. F(x, y, y , y ) 0 – общий вид обыкновенного дифференциального уравнения 2-го порядка;
5. x 2 z 8 y z x 0 – уравнение в частных производных 1-го порядка;
x y
6.2 z 2 z 3y 0 – уравнение в частных производных 2-го порядка.
x 2 y
Решением дифференциального уравнения называется такая дифференцируемая
функция, которая при подстановке в уравнение обращает его в тождество.
1.1.1Дифференциальные уравнения в частных производных второго порядка
Многие задачи механики и физики приводят к исследованию дифференциальных уравнений с частными производными второго порядка. Так, например:
1) при изучении различных видов волн − упругих, звуковых, электромагнитных, а
также других колебательных явлений мы приходим к волновому уравнению
|
2 |
u |
|
|
2 |
u |
|
|
2 |
u |
|
|
2 |
u |
|
, |
||
|
a2 |
|
|
|
|
|||||||||||||
t |
2 |
|
x |
2 |
|
y |
2 |
|
z |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
где а − скорость распространения волн в данной среде; 2) процессы распространения тепла в однородном изотропном теле, так же как и
явления диффузии, описываются уравнением теплопроводности:
u |
a |
|
|
|
2 |
u |
|
2 |
u |
2 |
u |
|
|||
2 |
|
|
|
, |
|||||||||||
t |
|
|
|
|
x |
2 |
|
y |
2 |
z |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|||||||
3) при рассмотрении установившегося теплового состояния в однородном изотропном |
|||||||||||||||
теле мы приходим к уравнению Пуассона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2u |
|
2u |
|
2u |
f (x, y, z) . |
||||||||||
x2 |
y 2 |
|
z 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
При отсутствии источников тепла внутри тела уравнение данное переходит в |
|||||||||||||||
уравнение Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2u |
|
2u |
|
2u |
0 . |
|
||||||||
|
x2 |
|
y 2 |
z 2 |
|
||||||||||
|
|
|
|
|
|
|
|||||||||
Потенциалы поля тяготения и стационарного электрического поля также удовлетворяют уравнению Лапласа, в котором отсутствуют массы и, соответственно,
электрические заряды.
2
Приведенные уравнения называют основными уравнениями математической физики.
Их подробное изучение дает возможность построить теорию широкого круга физических явлений и решить ряд физических и технических задач.
Функция u u(x, y, z) , удовлетворяющая какому-либо из приведенных уравнений,
называется его решением.
1.1.2Понятие об общем решении уравнения в частных производных
Рассмотрим |
обыкновенное |
дифференциальное |
уравнение |
n-го порядка: |
|||
|
|
(n) |
) . Его общий интеграл представляет собой некоторое семейство функций, |
||||
f (x, y, y , y ,..., y |
|
||||||
зависящее |
от n |
произвольных постоянных F (x, y,C1 ,C2 ,..., Cn ) . Любое частное решение |
|||||
получается из него, если параметрам C1 ,C2 ,..., Cn |
придать определенные значения. |
|
|
||||||
Рассмотрим решения некоторых дифференциальных уравнений в частных |
|||||||||
производных. |
|
|
|
|
|
|
|
|
|
Пример 1. Пусть дано уравнение |
2u |
0 |
, где u u(x, y) . |
|
|
|
|
|
|
x y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Решение: найдем его общий интеграл, т.е. функцию u u(x, y) , |
удовлетворяющую |
||||||||
|
|
|
|
|
|
|
u |
|
|
данному уравнению. Для этого сначала |
запишем это уравнение в |
виде: |
|
|
|
0 . |
|||
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
|
Поскольку производная по переменной х от величины, стоящей в скобках, равна нулю, то
последняя является некоторой произвольной функцией |
от у: |
|
|
f ( y) . Поэтому |
|
|
|||
|
y |
|||
u(x, y) f ( y)dy . Но интегрируя произвольную функцию |
f ( y) , |
получим новую, также |
||
произвольную функцию, скажем F ( y) , плюс произвольная функция g(x) ( g(x) играет роль произвольной постоянной интегрирования в теории обыкновенных дифференциальных уравнений). Таким образом, общий интеграл уравнения второго порядка u(x, y) g(x) F( y)
содержит две произвольные функции.
Пример 2. Решить уравнение z 1, где z z(x, y) .
x
Решение: проинтегрируем обе части уравнения по х:
z
x dx 1 dx x f ( y) ,
где f ( y) – произвольная функция.
3

Пример 3. Решить уравнение 2 z 6 y , где z z(x, y) .
y 2
Решение: проинтегрируем обе части уравнения по у:
|
|
|
|
2 z2 |
dy 6 ydy . |
|
|
|
|
|
y |
|
|
Получаем |
z |
3y 2 |
g(x) , где |
g(x) – произвольная функция. |
||
y |
||||||
|
|
|
|
|
||
полученное равенство:
z (3y 2 g(x))dy y3 yg(x)
Интегрируем повторно по у
h(x) ,
где g(x), h(x) – произвольные функции.
Пример 4. Решить уравнение |
2 z |
0 |
, где z z(x, y) . |
|
x y |
||||
|
|
|
Решение: проинтегрируем обе части уравнения сначала по х, а затем по у:
2 z dx z f ( y) ,
x y y
тогда
z f ( y)dy g(x) C1 ( y) g(x) ,
где g(x), h(x) – произвольные функции.
Замечание: в отличие от общего решения обыкновенного дифференциального уравнения, зависящего от произвольных постоянных, общее решение уравнения с частными производными зависит от произвольных функций, количество которых равно порядку уравнения.
Упражнения
Найти общее решение u u(x, y) следующих дифференциальных уравнений с частными производными. Выполнить проверку.
1.1 |
|
2u |
|
x y . |
|
|
|
||
|
x y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Ответ: |
u(x, y) |
x2 y |
|
xy2 |
C (x) C |
|
( y) . |
||
|
|
2 |
|||||||
|
|
|
2 |
2 |
1 |
|
|||
|
|
|
|
|
|
||||
1.22u x2 y .x2
Ответ: u(x, y) x4 yx2 xC1 ( y) C2 ( y) . 12 2
1.32u x y .y 2
Ответ: u(x, y) |
xy2 |
|
y3 |
|
yC (x) C |
|
(x) . |
||||||||||
|
|
|
|
|
2 |
||||||||||||
|
|
|
|
|
2 |
|
|
|
6 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.4 |
|
2u |
|
|
1 u |
0 . |
|
|
|
|
|||||||
|
x y |
|
x |
|
y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: |
u(x, y) C (x) |
1 |
C |
|
( y) . |
|
|
||||||||||
|
2 |
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4
1.5 |
2u |
2 y |
u |
. |
|
x y |
x |
||||
|
|
|
Ответ: u(x, y) C1 (x)ey2 C2 ( y) .
1.6 |
|
2u |
|
|
5 |
u |
. |
|
|
|
|
|
|
|
x y |
|
y |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
u(x, y) C |
(x) C |
2 |
( y)e5 x . |
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
||
1.7 |
|
2u |
2 . |
|
|
|
|
|
|
|
|||
|
x2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
u(x, y) x2 |
C ( y)x C |
2 |
( y) . |
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1.8 |
|
2u |
|
|
2x . |
|
|
|
|
|
|
||
|
x y |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
u(x, y) x2 y C ( y) C |
2 |
(x) . |
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1.92u u .y 2 y
Ответ: u(x, y) C1 (x)e y C2 (x) .
1.102u e x y .
y 2
Ответ: u(x, y) ex y yC1 (x) C2 (x) .
1.112u 6x .x2
Ответ: |
u(x, y) x3 xC |
( y) C |
2 |
( y) . |
||
|
|
|
1 |
|
|
|
1.12 |
|
2u |
sin y |
|
|
|
|
x y |
|
|
|
||
|
|
|
|
|
|
|
Ответ: u(x, y) x cos y C1 (x) C2 ( y) .
1.2Начальные и граничные условия. Задача Коши
1.2.1Задача Коши для дифференциальных уравнений первого порядка
Будем рассматривать случай, когда искомая функция u зависит от двух переменных u u(x, y) . Тогда уравнение первого порядка будет иметь вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x, y, u, u x |
, u y ) 0 . |
|
|
|
|
|
|
|
|||
|
Всякое решение |
u u(x, y) |
данного |
уравнения будем |
называть |
интегральной |
||||||||||
поверхностью (график решения – поверхность в пространстве с координатами x, y,u ). |
||||||||||||||||
|
Для того чтобы из совокупности всех решений данного уравнения выделить |
|||||||||||||||
некоторое |
частное |
решение, |
формулируется |
задача |
Коши: найти |
решение |
уравнения |
|||||||||
|
|
|
удовлетворяющее |
условию |
u(x0 , y) |
|
( y) , |
где |
( y) |
– |
некоторая |
|||||
|
|
|||||||||||||||
F (x, y, u, u x |
, u y ) 0 , |
|
||||||||||||||
заданная функция. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Обозначим через |
l |
кривую |
в |
пространстве |
x, y,u , задаваемую |
уравнениями: |
|||||||||
x x0 , |
u ( y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда задача Коши имеет следующий геометрический смысл: среди всех |
|||||||||||||||
интегральных поверхностей найти ту, которая проходит через заданную кривую l. |
|
|||||||||||||||
2
1.2.2Задача Коши для дифференциальных уравнений второго порядка
Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за x x0 . В результате возникает задача Коши:
F (x, y,u,u |
,u |
,u |
,u |
,u |
) 0, |
|
|
x |
y |
xx |
yy |
xy |
|
|
|
|
|
|
|
|
u(x0 , y) ( y), |
|
|
|
|||
|
(x0 , y) ( y). |
|
|
|
||
u y |
|
|
|
|||
Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для
нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные
(зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости,
или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая
влияния концов, мы тем самым не будем учитывать влияния отраженных волн.
|
a |
2 |
|
задаются два начальных условия: u(x,0) (x) и |
Для волнового уравнения utt |
|
uxx |
ut (x,0) (x) . Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие – начальные скорости точек струны. В случае
|
a |
2 |
|
на плоскости или в пространстве задаются те же два |
волнового уравнения utt |
|
uxx |
начальных условия, только функции φ и ψ, соответственно, будут зависеть от двух или трех переменных.
2
Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются
граничными условиями или краевыми условиями. Если в задаче заданы начальные и
граничные условия, то такая задача называется смешанной. |
|
Для уравнения колебаний струны часто задаются условия: u(0,t) 0, |
u(l,t) 0 . Эти |
условия физически означают, что концы струны закреплены (то есть отклонения при x 0 и
при x l в любой момент времени равны нулю). Можно задавать и другие условия на
|
(0,t) 0, |
|
(l,t) 0 |
– свободные концы струны. |
концах струны, например, ux |
ux |
1.3Классификация уравнений второго порядка в частных производных
Рассмотрим уравнение второго порядка
|
2 z |
|
2 z |
|
2 z |
|
z |
|
z |
|
|
||
a |
|
2 |
2b |
|
c |
|
2 |
F x, y, z, |
|
, |
|
0 , |
(1) |
|
|
|
|
||||||||||
|
x |
|
x y |
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
x y |
|
|
|||||
где a a(x, y), b b(x, y), c c(x, y) .
Обозначим D b2 ac . Тогда уравнение (1) принадлежит
кгиперболическому типу, при D 0 ,
кпараболическому типу, при D 0 ,
кэллиптическому типу, при D 0.
К уравнениям гиперболического типа приводят различные задачи о колебательных процессах. Уравнения параболического типа описывают процессы распространения тепла,
диффузии и т.п. К уравнениям эллиптического типа обычно приводят задачи о стационарных тепловых процессах.
Упражнения
1.13 |
К какому типу относится уравнение колебания струны |
2u |
a 2 |
2u |
? |
|
t 2 |
x 2 |
|||||
|
|
|
|
|||
Ответ: гиперболическому. |
|
|
|
|
||
1.14 |
К какому типу относится уравнение теплопроводности |
u |
a 2 |
2u |
? |
|
t |
x 2 |
|||||
|
|
|
|
|||
Ответ: параболическому.
1.15 К какому типу относится уравнение Лапласа 2u 2u 0 ?
y 2 x2
Ответ: эллиптическому.
3
Глава 2. Уравнение колебания струны
2.1Вывод уравнения колебания струны
Рассмотрим натянутую струну длины l закрепленную на концах. В положении равновесия струна направлена вдоль оси Ox. Сила натяжения T0, действующая на струну,
предполагается значительной. Каждую точку струны длины l можно охарактеризовать значением еѐ абсциссы x и смещением этой точки в момент времени t.
Для упрощения задачи примем следующие предположения:
1. Будем рассматривать только поперечные колебания струны, предполагая, что движение происходит в одной плоскости, и что все точки струны движутся перпендикулярно оси Ox.
Тогда процесс колебания струны может быть описан одной скалярной функцией u(x,t) , которая характеризует (вертикальное) смещение точки струны с координатой x в
момент времени t.
2. Будем рассматривать струну как гибкую упругую нить:
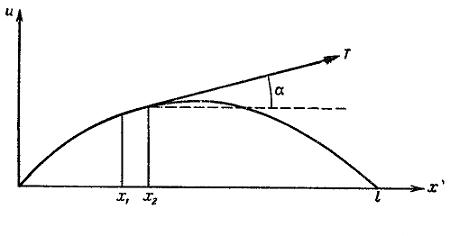
Математической выражение понятия гибкости заключается в том, что напряжения, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю (рис.1). Это условие выражает собой то, что струна не сопротивляется изгибу.
Понятие "нить" означает, что мы пренебрегаем формой поперечного сечения и толщиной (рассматриваем линейную плотность ρ(x)).
Рис. 1. Профиль струны
3. Рассматриваем только малые колебания струны, т.е. будем считать, что смещение
u(x,t) , а также u (x, t) столь малы, что квадратами этих величин по сравнению с 1 можно
x
пренебречь, то есть u2 (x,t) 1, u 2 (x, t) 1 .
x
4
4. Величина напряжений (силы натяжения) может быть вычислена с помощью закона Гука: сила натяжения, возникающая в струне, пропорциональна еѐ относительному удлинению:
l T ~ x ,
где x - начальная длина струны, l - удлинение струны, таким образом,
T k xl ,
где k – коэффициент упругости.
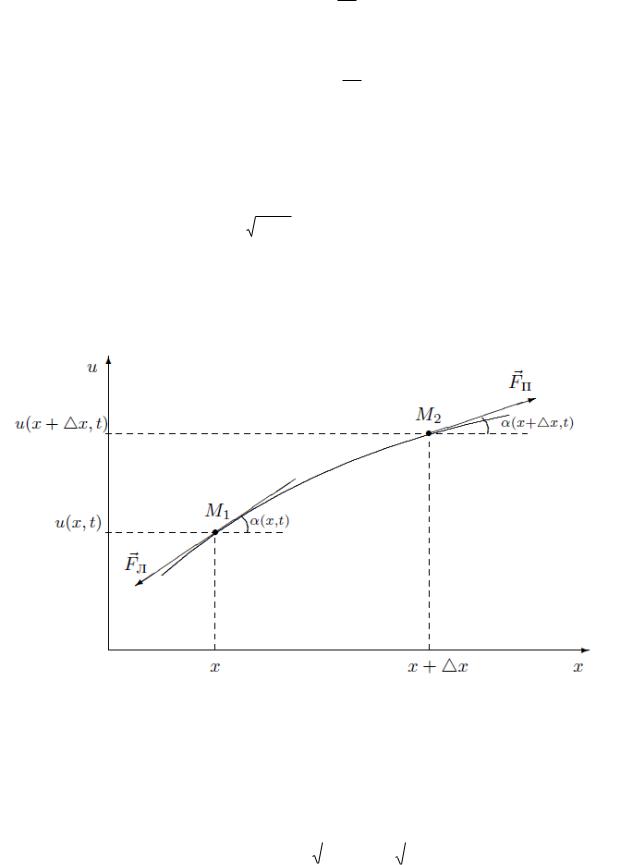
Длина произвольного участка М1М 2 струны (рис.2) в любой момент времени выражается формулой:
x x
l
x
x x
1 u dx dx x x x x .
x
x
Таким образом, получаем, что при условии малых отклонений длина произвольного участка струны сохраняется. А значит, можно считать, что величина сил натяжения точек струны не изменяется с течением времени, т.е. имеем T (x,t) T (x) .
Рис.2. Мгновенный профиль участка струны (x, x x) в момент времени t
Покажем также, что натяжение не зависит и от x. Найдем проекции натяжения на оси x и u (обозначим их Tx и Tu):
Tx |
(x) T (x) cos |
|
T (x) |
|
|
|
T (x) |
|
T (x) , |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
1 tg 2 |
1 u 2 |
|||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
5

|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
ux |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tu (x) T (x) sin T (x) |
1 tg 2 |
|
T (x) |
1 u 2 |
|
T (x) ux |
, |
||
|
|
|
|
|
|
x |
|
|
|
где α – угол касательной к кривой) u(x,t) с осью x. |
|
|
|
|
|
|
|
||
На участок (x, x x) действуют силы натяжения и внешние силы. Сумма проекции |
|||||||||
всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания,
т.е. струна не движется вдоль оси Ох). Так как внешние силы по предположению направлены вдоль оси u, то
Tx (x x) Tx (x) 0 или Tx (x x) Tx (x) .
Отсюда в силу произвольности x и x следует, что натяжение не зависит от x, т. е.
для всех значений x и t:
T (x) T0 .
Согласно второму закону Ньютона сумма сил, действующих на участок струны М1М 2
(рис.2) равна по величине и по направлению вектору ускорения этого участка, умноженному на его массу. Определим величины всех сил, действующих на этот участок. Обозначим через
F (x, t) плотность распределения внешних сил, вызывающих отклонение точек струны
только в вертикальном направлении. Тогда величина внешних сил, действующих на участок
М1М 2 , при условии непрерывности функции F (x, t) по переменной х равна:
x x |
|
|
|
|
|
|
|
F( , t)d F(x1 , t) x, |
x1 (x, x x). |
|
|||
|
|
|||||
x |
|
|
|
|
|
|
Далее, силы натяжения Fл |
T (x) |
и Fп T (x x) , действующие со стороны левого (в |
||||
точке М1 ) и правого (в точке М 2 ) |
концов струны, направлены |
по касательным к |
||||
мгновенному профилю струны в соответствующих точках. |
|
|
||||
Для вертикальной составляющей сил натяжения имеем выражение |
|
|||||
|
|
T0 sin (x x,t) T0 sin (x,t) 0 . |
|
|||
Так как рассматриваем малые колебания, то |
|
|
|
|||
T0 sin (x x,t) T0 sin (x,t) T0tg (x x,t) T0tg (x,t) |
||||||
|
|
|
|
,t) x, |
x2 (x, x x). |
|
T0 (ux (x x,t) ux (x,t)) T0uxx (x2 |
||||||
Таким образом, сумма сил, действующих на участок струны М1М 2 |
равна: |
|||||
|
|
(x2 ,t) x F (x1 ,t) x. |
|
|
(2) |
|
FM1M 2 T0uxx |
|
|
||||
С другой стороны, рассматривая участок струны как совокупность материальных точек, имеем
6
