Вопрос 37. Интеграл с переменным верхним пределом, его непрерывность.

Пусть функция f(x) интегрируема на [a,b]. Тогда, ∀x∈[a,b] каково бы ни было число x из [a,b], функция f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция , которую называют интегралом с переменным верхним пределом.

Непрерывность F(x). Если функция f(x) интегрируема на интервале (a,b) ( =>интегрируема на любом сегменте, содержащихся в интервале (a,b)), то интеграл с переменным верхним пределом представляет собой непрерывную на (a,b) функцию от верхнего предела. Чтобы убедиться в этом, докажем, что приращение ΔF(x)=F(x+Δx)−F(x)  функции 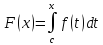стремится к нулю при Δx→0 .  В силу формулы среднего значения имеем  где μ заключено между точной верхней и нижней гранями  функции f(x) на сегменте [x,x+Δx]. Из последней формулы и вытекает, что ΔF→0  при Δx→0 . =>непрерывна в каждой точке интервала(a,b).

Вопрос 38. Дифференцируемость интеграла с переменным верхним пределом.

Пусть функция f(x) интегрируема на [a,b]. Тогда, ∀x∈[a,b] каково бы ни было число x из [a,b], функция f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция , которую называют интегралом с переменным верхним пределом.

Дифференцируемость F(x). Если f интегрируема на [a,b] и непрерывна в x0∈[a,b] , то Fдифференцируема в x0 иПри доказательстве теоремы было установлено существование производной от интеграла с переменным верхним пределом и доказано, что эта производная равна значению подынтегральной функции в точке, равной верхнему пределу, то есть

Доказательство Докажем что 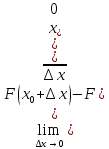Для этого оценимЗаметим, чтои => , ==(1) Пусть задано ε>0. В силу непрерывности f в точке х0 ∃δ(ε)>0 , что если ∣x−x0∣   <δ , и x∈[a,b]⇒∣f(x)−f(x0) ∣  <ε  (2) Выберем Δx так что ∣Δx∣<δ , тогда для значений t на отрезке по которому ведется интегрирование, будем иметь  ∣  t−x0 ∣  ≤∣Δx∣<δ⇒ из (1)и(2) получим   ≤ =ε.  Последнее означает, что Чтд

Вопрос 39. Формула Ньютона-Лейбница.

Функция непрерывна на отрезке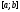, тогда она имеет первообразную. Пусть- её произвольная первообразная. Тогда.

Доказательство:

Функция 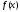непрерывна на отрезке,- первообразная функции,

, ,

. Теорема доказана.

Вопрос 40. Замена переменной в определенном интеграле.

При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.

теорема Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t[α,β].

Тогда справедливо следующее равенство:

Эта формула носит название формулы замены переменной в определенном интеграле.

Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).