Вопрос 21. Достаточное условие экстремума функции, имеющей n-ную производную.

Вопрос 22.

Выпуклость и вогнутость прямой. Точки перегиба.

Определение: По определению кривая называется выпуклой вниз (вверх) на отрезке [a,b], если любая дуга этой кривой с концами в точках () расположена не ниже (не выше) стягивающей ее хорды.

Определение: Множество называется выпуклым, если для любых двух точек этого множества, отрезок, соединяющий их лежит также в этом множестве.

Выпуклость вверх Выпуклое множество

Выпуклость вниз Невыпуклое множество

Теорема 1 (необходимое и достаточное условие выпуклости на отрезке)

Пусть функция непрерывна на [a,b] и имеет вторую производную на (a,b). Для того чтобы кривая была выпуклой кверху (книзу) на [а,b], необходимо и достаточно, чтобы выполнялось неравенство () для всех.

Доказательство:

Пусть наша кривая выпукла кверху на [a,b]. Тогда для любых х и h >0 таких, что х, х+2h[a,b], имеет место неравенство , откуда.

Если теперь 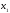и- произвольные точки интервала (a,b), то, положив h = (-)/n, будем иметь

.

Таким образом, (, и, переходя к пределу при, получим неравенство, показывающее, что производнаяна интервале (a,b) не возрастает. Но тогда на (a,b).

Обратно, пусть и. Нам нужно доказать, что функция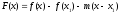, где, удовлетворяет неравенству. Допустим, что это не так. Тогда. Поэтому.

Применяя формулу Тейлора, получим

0=. Но в правой части этой цепочки равенств первый член по предположению отрицательный, а второй неположительный, поэтому правая часть меньше нуля, и мы пришли к противоречию.

Доказательство в случае Определение.

Точка называется точкой перегиба, если в этой точке график переходит через сторону касательной ( разные выпуклости слева и справа).

Замечание.

Точка перегиба существует только если . Пример

Теорема 1 (Достаточное условие существования точки перегиба).

Если функция имеетнепрерывной в точке,=0 и, тоточка перегиба.

Доказательство:

В этом случае: ,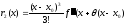(формула Тейлора) , или.

В силу непрерывности ви того факта, чтосохраняет знак в некоторой окрестности точки. С другой стороны, множительменяет знак при переходечерез, а вместе с ним и величина(равная превышению точки кривой над касательной в) меняет знак при переходечерез.

Теорема доказана.

Вопрос 23.

Асимптоты функции.

Определение: Прямая называется наклонной асимптотой функцииf(x) при , еслиf определена в окрестности точки и расстояние между графиком и прямой стремится к нулю.

Уравнение наклонной асимптоты:

Пусть- асимптота при

, ,,

, ,,значит ,

Замечание: возможен случай, когда k существует, а b – нет, в этом случае асимптот нет!

Вопрос 24.

Первообразная. Теорема о первообразной.

Определение 1: Функция F называется первообразной функции f на интервале (a,b), если функция f непрерывна на интервале (a,b), и для всех x из этого интервала выполняется равенство: F΄(x)=f(x).

Замечание: Вместо (a,b) можно рассматривать [a,b], (a,b] и [a,b), но нужно будет говорить про односторонние производные: 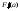=f(a), и=f(b).

Пример

.

на промежутке (-∞,0) и на (0,+∞).

Теорема:(О множестве всех первообразных).

Пусть F(x) является первообразной функции f(x) на на промежутке I, тогда функции вида F(x)+C и только они являются первообразными функции f(x), где C – произвольная константа.

Доказательство:

Пусть функция F(x) – первообразная функции f(x), тогда F΄(x)=f(x) и (F(x)+C)΄=f(x). Пусть функции F и G – первообразные функции f(x) на промежутке I (нужно доказать, что они отличаются на константу). Тогда (F-G)΄=0F-G=C (по теореме о функции, имеющей нулевую производную).

Теорема доказана.

Свойства первообразных.

1. Пусть функция f(x) имеет первообразную F(x) на промежутке I и функция g(x) имеет первообразную G(x) на промежутке I, тогда функция f(x)±g(x) будет иметь первообразную F(x)±G(x) на промежутке I.

2. Первообразной функции k·f(x) является функция k·F(x).

3. Первообразной производной функции f΄(x) является сама функция f(x).