
- •Вопрос 1. Определение производной, ее геометрический смысл.
- •Вопрос 2. Непрерывность функции, имеющей производную.
- •Вопрос 3. Производная суммы, произведения, частного.
- •Вопрос 4. Производная обратной функции.
- •Вопрос 5. Определение дифференцируемости функции. Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке, необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Вопрос 6. Дифференциал. Его геометрический смысл.
- •Вопрос 7. Производная сложной функции.
- •Вопрос 8. Производная высших порядков. Дифференциал высших порядков.
- •Вопрос 9. Дифференцирование параметрически заданной функции.
- •Вопрос 10. Теорема Ферма. Ее геометрический смысл.
- •Вопрос 11 Теорема Ролля. Ее геометрический смысл.
- •Вопрос 13. Теорема о среднем Лагранжа. Ее геометрический смысл.
- •Вопрос 14.
- •Раскрытие неопределенностей вида ,,,,.
- •Вопрос 15. Разложение многочлена по степеням (х-а)
- •Вопрос 16. Формула Тейлора с остаточным членом в форме Лагранжа.
- •Вопрос 17.
- •Вопрос 21. Достаточное условие экстремума функции, имеющей n-ную производную.
- •Вопрос 22.
- •Выпуклость и вогнутость прямой. Точки перегиба.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Вопрос 25. Неопределенный интеграл. Его свойства.
- •Вопрос 26. Метод внесения под знак дифференциала. Метод подстановки.
- •Вопрос 27. Интегрирование по частям.
- •Вопрос 28. Интегрирование рациональных дробей.
- •Вопрос 29.
- •Вопрос 31. Интегральная сумма, ее предел. Определение определенного интеграла.
- •Вопрос 32. Необходимое условие интегрируемости.
- •Вопрос 33. Суммы Дарбу. Их свойства.
- •Вопрос 34.
- •Вопрос 37. Интеграл с переменным верхним пределом, его непрерывность.
- •Вопрос 38. Дифференцируемость интеграла с переменным верхним пределом.
- •Вопрос 39. Формула Ньютона-Лейбница.
- •Вопрос 40. Замена переменной в определенном интеграле.
- •Вопрос 41. Интегрирование по частям определенного интеграла.
- •Вопрос 42. Теорема о среднем для определенного интеграла.
- •Вопрос 43. Непрерывная и гладкая прямая, заданная параметрически. Длина этой кривой.
- •Вопрос 44. Площадь фигуры, заданной в полярной системе координат.
- •Вопрос 45. Объем тел вращения.
Раскрытие неопределенностей вида ,,,,.
Кроме
рассмотренных неопределенностей
 и
и ,
встречаются неопределенности вида
,
встречаются неопределенности вида ,
, ,
, ,
,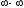 ,
, ,
определение которых очевидно. Эти
неопределенности сводятся к
неопределенностям
,
определение которых очевидно. Эти
неопределенности сводятся к
неопределенностям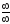 или
или алгебраическими преобразованиями.
алгебраическими преобразованиями.
Неопределенность
 (
( при
при
 ).
).
Ясно,
что
 или
или
 .
.
Неопределенности вида
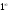 ,
, ,
, для выражения
для выражения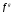 сводятся
к неопределенности
сводятся
к неопределенности .
.
Согласно
определению этой функции
 .
. ,
то
,
то .
.
Неопределенность
 (
( ,
, ,
, при
при )
)
Легко
видеть, что
 .
.
Вопрос 15. Разложение многочлена по степеням (х-а)
Рассмотрим произвольный многочлен степени n:
(1) 
Пусть
a
– любое фиксированное число, тогда,
полагая
 ,
получим
,
получим
(2) 
Это
выражение называют разложение многочлена
 по степеням
по степеням .
Здесь
.
Здесь – числа, зависящие от
– числа, зависящие от и
и ,
– коэффициенты разложения
,
– коэффициенты разложения
 по степеням
по степеням .
.
Подставим
в выражение (2)
 ,
получим
,
получим
(3) 
Найдем
последовательные производные
 и подставим в ним
и подставим в ним


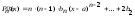



Таким
образом, многочлен
 может быть представлен в виде
может быть представлен в виде

или

Последняя
формула называется формулой Тейлора
для многочлена
 по степеням
по степеням .
Отметим, что правая часть этого выражения
фактически не зависит от
.
Отметим, что правая часть этого выражения
фактически не зависит от .
.
Вопрос 16. Формула Тейлора с остаточным членом в форме Лагранжа.
Если
функция f(x)
n
раз дифференцируема в точке а, то для
нее существует многочлен
 - это многочлен Тейлораn-го
порядка функции f(x)
в точке a.
Обозначим за
- это многочлен Тейлораn-го
порядка функции f(x)
в точке a.
Обозначим за
 - на сколько многочлен отличается от
самой функции.
- на сколько многочлен отличается от
самой функции. называют остаточным членом. Нужно
доказать, что для «хороших» функций
называют остаточным членом. Нужно
доказать, что для «хороших» функций будет достаточно мало. Докажем теорему,
которую сформулируем в конце. =))
будет достаточно мало. Докажем теорему,
которую сформулируем в конце. =))
Рассмотрим функцию f; зафиксируем точку a, в которой будем раскладывать функцию, и произвольную точку x, такую что f(x) n-1 раз дифференцируема на [a,x] и n раз дифференцируема на (a,x). В точке а функция дифференцируема n-1 раз, значит для нее можно составить многочлен Тейлора n-1 порядка.

Представим
 в
виде:
в
виде: ,
где р – произвольное число,H
– некоторая функция, зависящая от x.
,
где р – произвольное число,H
– некоторая функция, зависящая от x.
Рассмотрим
функцию :


Рассмотрим
F(u)
на [a,x]:
F(u)
непрерывная на [a,x],
дифференцируема на (a,x),
F(x)=F(a)
 по
теореме Ролля
по
теореме Ролля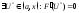
 ;
продифференцируем:
;
продифференцируем:
 -
и почти все взаимно уничтожается.
-
и почти все взаимно уничтожается.






 ,
тогда
,
тогда

 ;
;
 Подставим
теперьp:=n;
Подставим
теперьp:=n;
 -
это остаточный член в форме Лагранжа.
-
это остаточный член в форме Лагранжа.
Вопрос 17.
Остаточный член в форме Пеано.
Рассмотрим форму Лагранжа:
Пусть теперь f имеет непрерывную n-ю производную в точке а. Это означает, что на [a,x) функция n раз дифференцируема. Значит f(x) можно представить в виде:
 ;
;

 ,
т.к. производная непрерывна. Тогда
,
т.к. производная непрерывна. Тогда
 можно представить в виде:
можно представить в виде:
 ;
;

 -
это формула Тейлора с остаточным членом
в форме Пеано.
-
это формула Тейлора с остаточным членом
в форме Пеано.
Вопрос 18.
Ряд Тейлора, его сходимость, признак сходимости.
Вопрос 19.
Экстремум функции. Необходимое условие экстремума непрерывной функции.
Рассмотрим
график непрерывной функции y=f(x),
изображенной на рисунке. Значение
функции в точке x1 будет больше
значений функции во всех соседних точках
как слева, так и справа от x1. В этом
случае говорят, что функция имеет в
точке x1 максимум. В точке x3 функция,
очевидно, также имеет максимум. Если
рассмотреть точку x2, то в ней значение
функции меньше всех соседних значений.
В этом случае говорят, что функция имеет
в точке x2 минимум. Аналогично для
точки x4.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0).
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Теорема 1. (Необходимое условие существования экстремума.)
Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство.
Пусть для определенности в точке x0 функция
имеет максимум. Тогда при достаточно
малых приращениях Δx имеем f(x0+
Δx)<f(x0), т.е. ![]() Но
тогда
Но
тогда
![]()
Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x0) ≥ 0 а при Δx → 0 + 0 f'(x0) ≤ 0. Так как f '(x0) определяет число, то эти два неравенства совместны только в том случае, когда f '(x0) = 0.
Вопрос 20.
Экстремум функции. Достаточное условие экстремума непрерывной функции.
Рассмотрим
график непрерывной функции y=f(x),
изображенной на рисунке. Значение
функции в точке x1 будет больше
значений функции во всех соседних точках
как слева, так и справа от x1. В этом
случае говорят, что функция имеет в
точке x1 максимум. В точке x3 функция,
очевидно, также имеет максимум. Если
рассмотреть точку x2, то в ней значение
функции меньше всех соседних значений.
В этом случае говорят, что функция имеет
в точке x2 минимум. Аналогично для
точки x4.
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Теорема 1: (первое достаточное условие существования экстремума)
Если
f(x)
дифференцируема в
 ,f’
имеет разные знаки слева и справа от Xo
=> Xo
– точка экстремума.
,f’
имеет разные знаки слева и справа от Xo
=> Xo
– точка экстремума.
Доказательство:
Т.к f(x) с одной стороны возрастает, с другой убывает, т.е.
 -
max
-
max
 -
min
-
min
Теорема доказана.
Теорема 2: (второе достаточное условие существования экстремума)
Если
в
 f(
f( )=0,f’’(
)=0,f’’( )>0
–min;
f’’(
)>0
–min;
f’’( )<0
–max
)<0
–max
Доказательство:
f’( )=0,
существуетf’’(
)=0,
существуетf’’( )=>f’
определена в U(
)=>f’
определена в U( )
)
f’(x)
в точке
 возрастает(f’’(
возрастает(f’’( )>0)
)>0)
f’(x)
в точке
 убывает(f’’(
убывает(f’’( )<0)
)<0)
1)
f’’( )>0f’(x)
возрастает, f’(
)>0f’(x)
возрастает, f’( )=0
=>
)=0
=>
при
x<

при
x< =>
=> – точка минимума
– точка минимума
2)
Аналогично для f’’( )<0…
)<0…
