
- •Вопрос 1. Определение производной, ее геометрический смысл.
- •Вопрос 2. Непрерывность функции, имеющей производную.
- •Вопрос 3. Производная суммы, произведения, частного.
- •Вопрос 4. Производная обратной функции.
- •Вопрос 5. Определение дифференцируемости функции. Необходимое и достаточное условие дифференцируемости.
- •Теорема 1: Для того, чтобы функция была дифференцируемой в точке, необходимо и достаточно , чтобы она имела конечную производную в этой точке.
- •Вопрос 6. Дифференциал. Его геометрический смысл.
- •Вопрос 7. Производная сложной функции.
- •Вопрос 8. Производная высших порядков. Дифференциал высших порядков.
- •Вопрос 9. Дифференцирование параметрически заданной функции.
- •Вопрос 10. Теорема Ферма. Ее геометрический смысл.
- •Вопрос 11 Теорема Ролля. Ее геометрический смысл.
- •Вопрос 13. Теорема о среднем Лагранжа. Ее геометрический смысл.
- •Вопрос 14.
- •Раскрытие неопределенностей вида ,,,,.
- •Вопрос 15. Разложение многочлена по степеням (х-а)
- •Вопрос 16. Формула Тейлора с остаточным членом в форме Лагранжа.
- •Вопрос 17.
- •Вопрос 21. Достаточное условие экстремума функции, имеющей n-ную производную.
- •Вопрос 22.
- •Выпуклость и вогнутость прямой. Точки перегиба.
- •Теорема 1 (Достаточное условие существования точки перегиба).
- •Вопрос 25. Неопределенный интеграл. Его свойства.
- •Вопрос 26. Метод внесения под знак дифференциала. Метод подстановки.
- •Вопрос 27. Интегрирование по частям.
- •Вопрос 28. Интегрирование рациональных дробей.
- •Вопрос 29.
- •Вопрос 31. Интегральная сумма, ее предел. Определение определенного интеграла.
- •Вопрос 32. Необходимое условие интегрируемости.
- •Вопрос 33. Суммы Дарбу. Их свойства.
- •Вопрос 34.
- •Вопрос 37. Интеграл с переменным верхним пределом, его непрерывность.
- •Вопрос 38. Дифференцируемость интеграла с переменным верхним пределом.
- •Вопрос 39. Формула Ньютона-Лейбница.
- •Вопрос 40. Замена переменной в определенном интеграле.
- •Вопрос 41. Интегрирование по частям определенного интеграла.
- •Вопрос 42. Теорема о среднем для определенного интеграла.
- •Вопрос 43. Непрерывная и гладкая прямая, заданная параметрически. Длина этой кривой.
- •Вопрос 44. Площадь фигуры, заданной в полярной системе координат.
- •Вопрос 45. Объем тел вращения.
Вопрос 29.
Интегрирование иррациональных функций.
Для
интегрирования иррациональной функции,
содержащей ![]() используется
подстановка
используется
подстановка![]() .
Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степеней x, применяется подстановка
в форме
.
Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степеней x, применяется подстановка
в форме![]() ,
где n полагается равным наименьшему
общему кратному знаменателей всех
дробных степеней, входящих в данную
функцию.
Рациональная функция x под
знаком корня n-ой степени, т.е. выражение
вида
,
где n полагается равным наименьшему
общему кратному знаменателей всех
дробных степеней, входящих в данную
функцию.
Рациональная функция x под
знаком корня n-ой степени, т.е. выражение
вида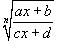 ,
интегрируется с помощью подстановки
,
интегрируется с помощью подстановки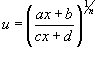 .
.
Вопрос 30.
Интегрирование тригонометрических функций.
Пусть
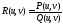
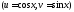 ,
где
,
где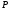 и
и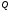 - многочлены от
- многочлены от и
и .
.
1)
Если один из многочленов
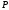 ,
,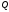 четный по
четный по ,
а другой – нечетный по
,
а другой – нечетный по ,
то подстановка
,
то подстановка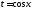 рационализирует интеграл.
рационализирует интеграл.
2)
Если один из многочленов
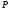 ,
,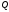 четный по
четный по ,
а другой – нечетный по
,
а другой – нечетный по ,
то подстановка
,
то подстановка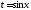 рационализирует интеграл.
рационализирует интеграл.
3)
Если оба многочлена четные по
 и
и ,
то подстановка
,
то подстановка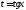 рационализирует интеграл.
рационализирует интеграл.
3’)
Выражения вида
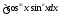 ,
где
,
где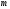 и
и - четные. Они сходны с 3 случаем, где
- четные. Они сходны с 3 случаем, где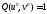
4) Универсальная подстановка.
Рационализация
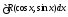 также достигается с помощью подстановки
также достигается с помощью подстановки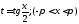 ,
которая называетсяуниверсальной.
В самом деле,
,
которая называетсяуниверсальной.
В самом деле,
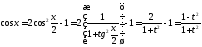 ;
;
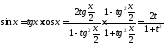 ;
;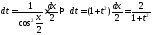
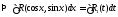 .
.
5)
Выражения вида
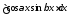 ;
;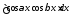 ;
;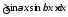 .
Они рационализируются с помощью перевода
в тригонометрические суммы.
.
Они рационализируются с помощью перевода
в тригонометрические суммы.
Вопрос 31. Интегральная сумма, ее предел. Определение определенного интеграла.
Пусть
задана функция f(x)
на отрезке
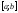 .
Составим разбиениеR:
.
Составим разбиениеR:
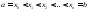 .
.
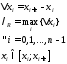
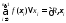
Это
интегральная сумма, соответствующая
разбиению R
и выбору точек
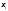 .
.
Если
существует предел при
 интегральных
сумм
интегральных
сумм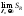 ,
и он не зависит отR
и
,
и он не зависит отR
и
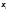 ,
то он называетсяопределенным
интегралом
,
то он называетсяопределенным
интегралом
Вопрос 32. Необходимое условие интегрируемости.
Теорема. Для того, чтобы функция f(x), определённая на отрезке [a,b], была интегрируема на нём, необходимо, чтобы она была ограничена на этом отрезке.
Доказательство. Предположим, что f(x) не ограничена на отрезке [a,b]. Тогда для каждого разбиения найдётся хотя бы один отрезок [xk−1,xk], на котором функция окажется неограниченной. Но тогда в интегральной сумме хотя бы одно слагаемое Δxkf(ξk) будет произвольно большим, и тогда последовательность интегральных сумм сходящейся быть не может. Значит, функция не интегрируема, что противоречит предполагаемому.
Вопрос 33. Суммы Дарбу. Их свойства.
Определение:
Пусть
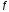 ограничена
на отрезке
ограничена
на отрезке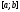 .
Введём разбиениеR
этого отрезка.
.
Введём разбиениеR
этого отрезка.
R:
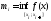 ,
,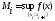 .
.
Тогда можем составить выражения:
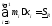 -
нижняя сумма Дарбу,
-
нижняя сумма Дарбу,
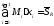 - верхняя сумма Дарбу.
- верхняя сумма Дарбу.
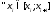 ,
,
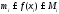 .
.
Пусть
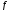 ограничена
на отрезке
ограничена
на отрезке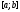 .
Введём разбиениеR
этого отрезка.
.
Введём разбиениеR
этого отрезка.
R:
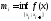 ,
,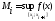 .
.
Тогда можем составить выражения:
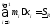 -
нижняя сумма Дарбу,
-
нижняя сумма Дарбу,
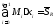 - верхняя сумма Дарбу.
- верхняя сумма Дарбу.
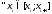 ,
,
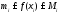 .
.
Свойства сумм Дарбу:
1)
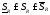 ,
для одного и того же разбиения.
,
для одного и того же разбиения.
2)
Рассмотрим два разбиения в случае, когда
одно разбиение является продолжением
другого. Т.е.
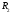 -
продолжение
-
продолжение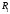 ,
если все точки
,
если все точки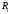 являются точками
являются точками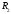 .
.
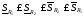
Добавление
точек не увеличивает
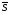 и не уменьшает
и не уменьшает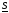 .
Пусть
.
Пусть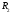 получается из
получается из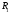 добавлением одной точки.
добавлением одной точки.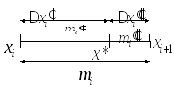
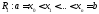 ,
,
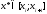 ,
,
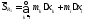 ,
,
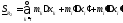 ,
,
Заметим,
что если
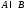 ,
то
,
то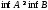 и
и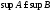 .
Отсюда заключаем:
.
Отсюда заключаем:
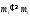 ,
,
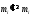 ,
,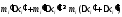 ,
,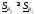 .
.
3)
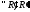
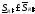 ,
,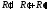 ,
,
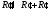 ,
,
=>
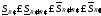 ,
т.е.
,
т.е.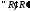
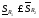 .
.
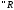
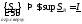 -
нижний интеграл (нижняя точная сумма
Дарбу).
-
нижний интеграл (нижняя точная сумма
Дарбу).
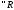
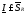 .
.
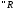
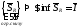 -
верхний интеграл (верхняя точная сумма
Дарбу).
-
верхний интеграл (верхняя точная сумма
Дарбу).
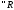
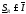 .
.
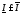 .
.
Вопрос 34.
Необходимое и достаточное условия интегрируемости функции.
Теорема:
Функция
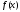 интегрируема на отрезке
интегрируема на отрезке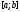 тогда и только тогда, когда
тогда и только тогда, когда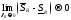 .
.
Доказательство:
Докажем необходимость условия:
Функция
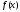 интегрируема на отрезке
интегрируема на отрезке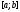 .
.
Пусть
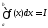 ,
тогда
,
тогда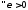
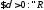
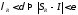 ,
т.е.
,
т.е.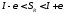 .
.
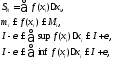
т.е.
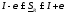 и
и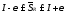 .
.
Далее
имеем:
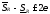 ,
т.е.
,
т.е.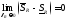 .
.
Необходимость доказана.
Докажем достаточность условия:
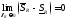 .
.
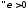
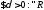
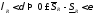 .
.
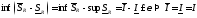 .
.
Докажем,
что
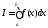 .
.
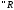
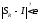 ,
,
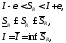
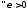
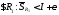 ,
,
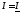 ,
тогда
,
тогда
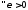
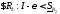 ,
т.е.
,
т.е.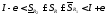 ,
,
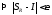 .
.
Достаточность доказана.
Вопрос 35.
Достаточное условие интегрируемости функции.
Теорема 1:
Если
функция
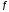 непрерывна на
непрерывна на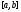 ,
то она интегрируема на
,
то она интегрируема на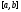 .
.
Доказательство:
Пусть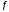 непрерывна на
непрерывна на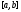 ;
тогда для разбиенияR,
у которого частичные отрезки
;
тогда для разбиенияR,
у которого частичные отрезки
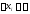 ,
имеет место (
,
имеет место (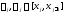 ).
).
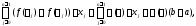
где
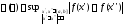 есть модуль непрерывности
есть модуль непрерывности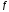 на
на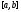 .
.
Поэтому
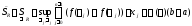 .
.
Но,
как мы знаем, для непрерывной на замкнутом
конечном отрезке
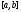 функции
функции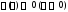 ,
поэтому для любого
,
поэтому для любого можно указать такое
можно указать такое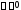 ,
что
,
что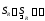 .
.
В
силу основной теоремы интеграл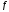 на
на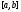 существует.
существует.
Теорема доказана.
Вопрос 36.
Свойства определенного интеграла.
Теорема 1: (Аддитивное свойство интегралов)
Функция
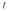 интегрируема на отрезке
интегрируема на отрезке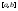 тогда и только тогда, когда
тогда и только тогда, когда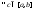 функция
интегрируема на отрезках
функция
интегрируема на отрезках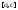 и
и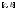 и при этом выполняется равенство:
и при этом выполняется равенство: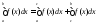
Доказательство:
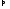 Пусть
Пусть
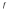 интегрируема на
интегрируема на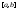 ,
тогда по основной теореме
,
тогда по основной теореме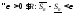
Можно
считать, что точка c
является точкой разбиения, потому что,
если она таковой не является, мы добавим
эту точку и рассмотрим новое разбиение
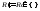 ,
тогда
,
тогда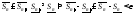 ,
поэтому можно считать, что разбиениеR
изначально содержит точку с. Тогда это
разбиение порождает разбиения
,
поэтому можно считать, что разбиениеR
изначально содержит точку с. Тогда это
разбиение порождает разбиения
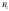 -
разбиение
-
разбиение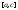 и
и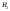 -
разбиение
-
разбиение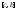 .
Тогда
.
Тогда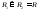 и разность сумм Дарбу можно представить
как:
и разность сумм Дарбу можно представить
как:
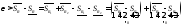 .
Так как каждое из этих двух слагаемых
неотрицательно и в сумме они меньше
.
Так как каждое из этих двух слагаемых
неотрицательно и в сумме они меньше
 ,
значит каждое из них меньше
,
значит каждое из них меньше
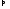 по
основной теореме
по
основной теореме интегрируема на
интегрируема на и
и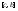 .
Доказано.
.
Доказано.
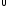 Пусть
Пусть
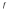 интегрируема на отрезках
интегрируема на отрезках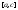 и
и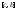 ,
тогда точно так же найдем
,
тогда точно так же найдем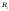 -
разбиение
-
разбиение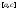 и
и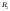 -
разбиение
-
разбиение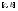 ,
такие что
,
такие что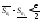 и
и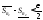 ,
тогда для разбиения
,
тогда для разбиения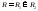
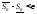 ,
гдеR–разбиение
отрезка
,
гдеR–разбиение
отрезка
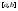 ,
,
значит
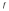 интегрируема на отрезке
интегрируема на отрезке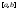 .
Доказано.
.
Доказано.
Доказали
интегрируемость, теперь докажем равенство
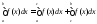 :
:
Замечание: Мы предполагаем, что точка с участвует во всех этих разбиениях; если она в них не участвует, то по следствию из основной теоремы нам это неважно, поскольку если хотя бы для одной последовательности разбиений предел стремится к числу, то и для всех остальных - тоже. И мы берем такую последовательность разбиений, что точка с в них участвует.
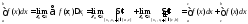
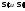 -
сумма берется по тем отрезкам, которые
содержатся в
-
сумма берется по тем отрезкам, которые
содержатся в
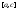 и
и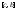 соответственно. Нужно учесть, что
соответственно. Нужно учесть, что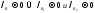 .
Теорема доказана.
.
Теорема доказана.
Замечание:
Мы определили понятие определенного
интеграла только для случая
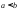 ;
доопределим понятие определенного
интеграла отa
до b
в случае, когда
;
доопределим понятие определенного
интеграла отa
до b
в случае, когда
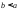 :
:
Если
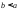 ,
то положим
,
то положим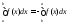 ,
тогда равенство
,
тогда равенство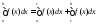 становится верным не только для
становится верным не только для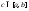 ,
но и для любых
,
но и для любых ,
при условии что все вышеперечисленные
интегралы существуют.
,
при условии что все вышеперечисленные
интегралы существуют.
Пример:
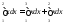
Теорема2: (Однородные свойства интегралов)
Пусть
функции
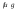 интегрируемы
на
интегрируемы
на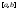 ,
тогда
,
тогда
f + g – интегрируема на
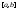 и
и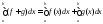 ,
если интегралы в правой части существуют,
т.е. в общем случае обратное не верно.
,
если интегралы в правой части существуют,
т.е. в общем случае обратное не верно.
(Пример:
Если взять f
– неинтегрируема на
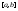 и –f
– тоже неинтегрируема, то их сумма =0 –
интегрируема).
и –f
– тоже неинтегрируема, то их сумма =0 –
интегрируема).
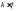 -
интегрируема на
-
интегрируема на
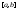 и
и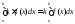 ,
обратное тоже верно, в случае если
,
обратное тоже верно, в случае если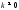
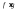 -
интегрируема.
-
интегрируема.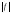 -
интегрируем
-
интегрируемЕсли
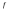 отделена от 0 на отрезке
отделена от 0 на отрезке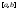 ,
т.е.
,
т.е.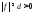 на
на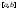 где
где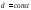 ,
то
,
то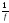 - интегрируема.
- интегрируема.
Доказательство:
1)
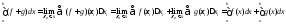
2) аналогично;
Замечание:
обозначим
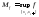 ;
;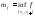 ;
;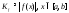 - по свойству ограниченности; соответственно
введем
- по свойству ограниченности; соответственно
введем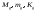
3)
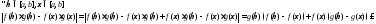
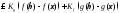
Перейдем
к супремумам: на произвольном промежутке
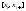
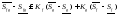
По
основной теореме найдутся такие разбиения
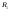 ,
что
,
что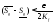 и
и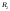 ,
что
,
что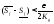 .
Теперь если мы возьмем сумму разбиений
.
Теперь если мы возьмем сумму разбиений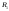 и
и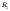 ,
то будут выполняться оба неравенства,
и тогда
,
то будут выполняться оба неравенства,
и тогда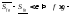 интегрируема.
интегрируема.
4)
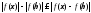 ;
переходя к супремумам и умножая на
;
переходя к супремумам и умножая на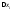 ,
получим:
,
получим:
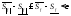
Замечание:
переход к супремуму на промежутке
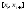 :
: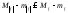
Замечание: обратное неверно:
Контрпример:
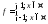 - сама по себе не интегрируема (доказано
ранее), а по модулю – интегрируема.
- сама по себе не интегрируема (доказано
ранее), а по модулю – интегрируема.
5)
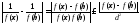 ;
переходя к супремумам супремум в этом
неравенстве, получим:
;
переходя к супремумам супремум в этом
неравенстве, получим:
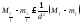 ;
теперь домножая на
;
теперь домножая на
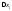 и суммируя, получим
и суммируя, получим
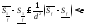
Теорема доказана.
