Вопрос 10. Теорема Ферма. Ее геометрический смысл.

Теорема Ферма: (Необходимое условие существования экстремума)

Если f(x) дифференцируема в точке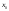и– точка локального экстремума, то.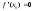

Доказательство:

Пусть f(x) возрастает в точке , т.е.

, т.е. – не точка экстремума.

Аналогично невозможен случай , следовательно.

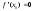Теорема доказана.

Геометрический смысл теоремы Ферма Существует такая точка , в которой касательная параллельна оси Ox.

Вопрос 11 Теорема Ролля. Ее геометрический смысл.

Теорема:

Если функция непрерывна на, дифференцируема наи, то существует точка, такая, что.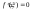

Доказательство:

Так как функция f непрерывна на [a,b], то существует точка x₁, в которой f достигает максимума и точка x₂, в которой f достигает минимума. Рассмотрим 2 случая:

1. Обе точки x₁ и x₂ совпадают с a или b, тогда

И тогда производная

2. Одна из точек не является концевой отрезка [a,b]. Пусть - та из них, которая, тогда в точкедостигается локальный экстремум, кроме того,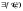, так как по условиюсуществует. Поэтому по теореме Ферма, что и требовалось доказать.

Контрпример 1

Уберем непрерывность в точке b: теорема потеряет силу.

Контрпример 2

Уберем дифференцируемость в одной из точек: теорема потеряет силу.

Теорема Ролля имеет простой геометрический смысл: если выполнены все условия теоремы, то на графике функции существует точкакасательная в которой параллельна осиx.

Вопрос 13. Теорема о среднем Лагранжа. Ее геометрический смысл.

Теорема:

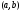Пусть функция непрерывна на отрезкеи имеет производную на интервале. Тогда существует на интервалеточка, для которой выполняется равенство

(1),

причем .

Доказательство:

В теореме Коши, возьмем . Тогда,,.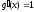

Из теоремы Коши: теорема доказана.

Физический смысл:

Найдется момент времени когда (средняя скорость равна мгновенной)

Геометрический смысл:

Теорема Лагранжа утверждает, что если кривая есть график непрерывной на функции, имеющей производную на, то на этой кривой существует точка, соответствующая некоторой абсциссетакая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривойи.

Равенство (1) называется формулой (Лагранжа) конечных приращений. Промежуточное значение удобно записывать в виде, гдеесть некоторое число, удовлетворяющее неравенствам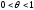. Тогда формула Лагранжа примет вид

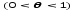
Она верна, очевидно, не только для , но и для.

Вопрос 14.

Правило Лопиталя. Раскрытие неопределенностей.

Правило Лопиталя. Случай 0/0.

Теорема 1: (Неопределенность вида 0/0)

Пусть f(x) и g(x) дифференцируемы в некоторой окрестности точки а,

в этой окрестности и в той же окрестности, тогда, если, то

Доказательство:

1) a – конечное.

Доопределим функции: f(a)=0 и g(а) = 0; f(x) и g(x) непрерывны на [a;x]

при

f(a)=g(a)=0 =>

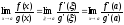
2)

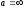
Пусть

Введем функции и

Теорема доказана.

Замечание: обратное неверно.

Пример:

Правило Лопиталя. Случай .

Теорема:

Пусть функции f и g определены и дифференцируемы в некоторой окрестности точки a иив некоторой выколотой окрестности точкиa, тогда, если

, то и

Доказательство:

Возьмем произвольную последовательность ,,, тогда по определению предела по Гейне

и

Тогда - дляf(x) определение предела вида |f(x)|>C, где C =

- аналогично для g(x)

Тогда можно найти такой номер, для которого будут выполняться оба неравенства:

,

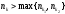
Используя термины можно записать:

,Пояснение: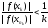, а т.к.

Найдем теперь предел отношения к:

[ можно добавить или отнять, предел от этого не изменится ]

[ воспользуемся теоремой Коши: или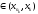- смотря, что больше]

- по определению предела по Гейне.

Мы получили еще не совсем теорему о сходимости последовательности через подпоследовательности, ( ее формулировка: если такова, что из любой её подпоследовательности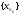можно извлечь в свою очередь подпоследовательность, сходящуюся к конечному или бесконечному А, то предел=А) мы пока что только из самой последовательности выделили сходящуюся подпоследовательность, а это еще не значит, что сама последовательность сходится.

Теперь возьмем произвольную последовательность и её произвольную подпоследовательность, тогда по только что доказанному из подпоследовательности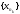мы можем выделить подпоследовательность, сходящуюся к, т. е.

Теперь мы взяли произвольную последовательность, поэтому

Причем важно, чтобы предел отношения производных существовал. Теорема доказана.