
41_5_Econometrics_Polyansky__Part_5
.pdf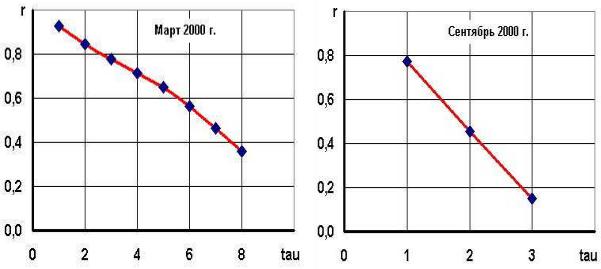
Полянский Ю.Н.
Эконометрика. Экономическое моделирование и прогнозирование.
цветом, шрифтом и т.п. |
|
|
|
|
|
|
Для обобщения значений выборочного коэффициента корреляции под |
||||
основной расчетной таблицей в ячейках A36:B44 составим итоговую табли- |
|||||
цу |
r(τ ) (рис.5.17). Значение r(τ =1 ) вычислим в ячейке B37 |
по формуле |
|||
«=D33/C34». Полученное значение r(τ =1 ) =0 ,9294 |
говорит |
о |
том, что |
||
между соседними членами временного ряда, сдвинутыми на лаг |
τ =1 (т.е. |
||||
на |
1 день) существует достаточно тесная связь. |
|
|
|
|
|
Однако с ростом величины лага связь обычно ослабевает. Аналогич- |
||||
ные вычисления проведем в следующих столбцах для других лагов. |
|||||
|
По полученным значениям |
r(τ ) построим коррелограмму (рис.5.18). |
|||
Как и предполагалось, она является убывающей функцией. Но скорость это- |
|||||
го |
убывания может быть различной. Анализ полученной коррелограммы |
||||
показывает, что в марте 2000 года курс доллара существенно зависел от его |
|||||
значений в предшествовавшие 1…4 |
дня. И лишь по истечении 4…5 |
дней за- |
|||
висимость ослабевала (т.е. r(τ ) |
становился <0,7…0,8). |
Обычно такое по- |
|||
ложение наблюдается, когда временной ряд без резких колебаний, относи- тельно стабильный (сравните с рис.5.6 задачи 5.1).
|
Рис. 5.18 |
Рис. 5.19 |
|
Для примера на рис.5.19 покажем аналогичную коррелограмму для |
|
сентября 2000 года. Вышеописанные расчеты можно и не проводить. Её |
||
можно легко получить, скопировав в ячейки построенной выше расчетной |
||
таблицы новые данные о курсе доллара за сентябрь 2000 года из задачи 5.3. |
||
|
Как видно, в сентябре 2000 года на курс доллара несколько влияло его |
|
значение только в предыдущий день. Далее эта взаимосвязь резко ослабева- |
||
ла. |
Скачки курса доллара в этот период были значительными (ср. с рис.5.10 |
|
задачи 5.3). Такое резкое убывание коррелограммы характерно для перио- |
||
дов значительной нестабильности в поведении объясняемой переменной. |
||
|
Задача 5.6 |
|
125

Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.
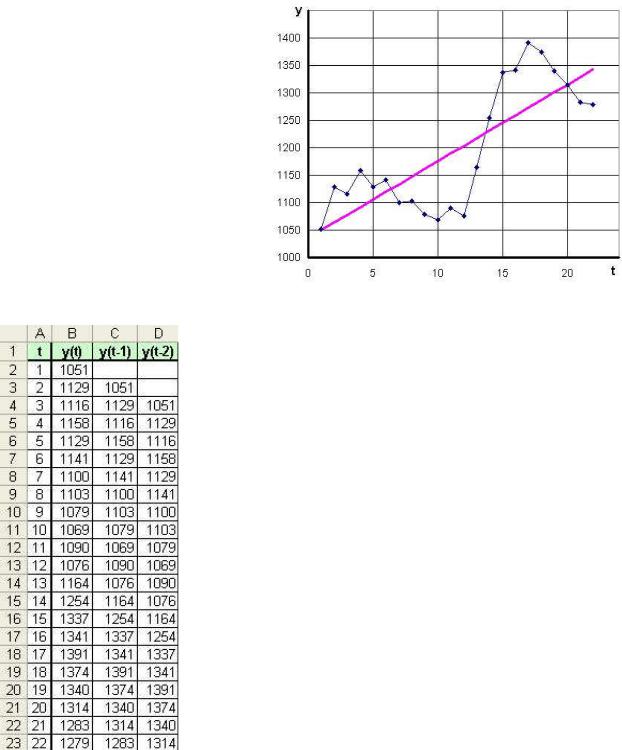
В таблице (рис.5.20) представлены данные о кур- |
||
се акций некоторой фирмы (руб.) за период 1…22 |
||
апреля. На основе приведенных данных, используя |
||
встроенные средства Microsoft Excel: |
||
1) |
построить классическую парную линейную мо- |
|
дель временного ряда yt = a + b t + εt ; оценить точ- |
||
ность и значимость модели в целом, значимость ко- |
||
эффициентов регрессии; получить точечный прогноз |
||
курса акций на 23 апреля того же года; сделать вывод |
||
о целесообразности использования такой модели; |
||
2) |
исследовать ряд на автокорреляцию; устранить |
|
её, построив авторегрессионную модель 1-го порядка |
||
AR(1) |
yt = b0 + b1 yt −1 |
+ εt ; выполнить аналогичные |
задания п.1; |
построить и исследовать авто- |
|
3) |
аналогично п.2 |
|
регрессионную модель 2-го порядка AR(2); |
||
4) |
сделать вывод о наиболее приемлемой модели |
|
из полученных выше. |
|
|
Решение.
1) Пользуясь инструментом «Регрессия» пакета ана- лиза Microsoft Excel (удобно вывести его на один лист с ис- ходными данными), получим следующую парную линей-
ную регрессионную модель приведенного временного ряда дробнее в задаче 5.1):
ˆyt = 1035,90 + 13,95 t .
Рис.5.20
(см. об этом по-
Полученная модель значима в целом ( F = 32 ,47 > F0 ,05 ;1; 20 = 4 ,35 ) и значим её коэффициент регрессии b ( tb = 5 ,70 > t0 ,95 ;20 = 2,09 ). Средняя от- носительная ошибка невелика ( A =5 ,02% ), т.к. имеем большие модули зна- чений объясняемой переменной. Однако корреляционной связь между пе- ременными слабая ( r =0 ,787 ). Качество модели очень низкое ( R2 =0 ,619 ,
R |
|
=0 ,600 ). Это вполне понятно, если взглянуть на общий вид графика |
ˆ |
2 |
|
временного ряда (рис.5.21). Моделью пользоваться нежелательно из-за её низкой точности.
Спрогнозируем курс акций на момент времени t =23 :
ˆy23 = 1035,90 + 13,95 23 = 1356,65 (руб.).
126
Полянский Ю.Н.
Эконометрика. Экономическое моделирование и прогнозирование.
2) Для таких временных рядов, в которых наблюдается сильная поло- жительная автокорреляция (проверьте самостоятельно по тесту Дарбина- Уотсона аналогично задаче 5.3), может оказаться более подходящей авторе- грессионная модель p -го порядка AR( p) вида
|
|
yt =bo |
+b1 yt−1 +b2 |
yt −2 +...+bp yt−p +εt , |
t =2,3,...,n. |
|
|||||||||
|
Она описывает изучаемый |
|
|
|
|
|
|
|
|
||||||
процесс в момент времени t |
в |
|
|
|
|
|
|
|
|
||||||
зависимости от его значений в |
|
|
|
|
|
|
|
|
|||||||
предшествовавшие |
|
|
|
моменты |
|
|
|
|
|
|
|
|
|||
времени t − 1 , t − 2 , …, |
|
t − p . |
|
|
|
|
|
|
|
|
|
||||
|
Построим по |
|
приведен- |
|
|
|
|
|
|
|
|
||||
ным данным авторегрессионную |
|
|
|
|
|
|
|
|
|||||||
модель 1-го порядка |
AR(1) (мар- |
|
|
|
|
|
|
|
|
||||||
ковского случайного процесса). |
|
|
|
|
|
|
|
|
|||||||
Она имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
yt =bo +b1 yt −1 +εt . |
|
|
|
|
|
|
|
|
|
|||||
|
Для |
этого |
в |
|
расчетной |
|
|
|
|
|
|
|
|
||
таблице |
добавим |
|
столбец |
C |
|
|
|
|
Рис. 5.21 |
|
|||||
(назовём его «y(t-1)») |
для значе- |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
ний объясняемой переменной в предшествовав- |
|||||||||
|
|
|
|
|
|
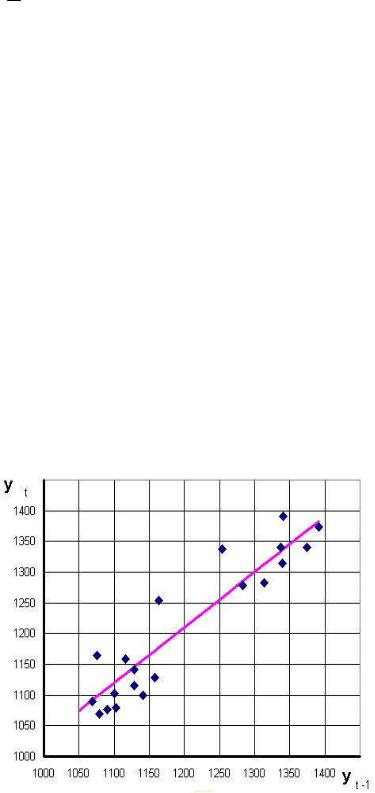
ший момент времени (рис.5.22). Скопируем в его |
|||||||||
|
|
|
|
|
|
ячейки C3:C23 данные из ячеек B2:B22, т.е. с |
|||||||||
|
|
|
|
|
|
временным сдвигом в |
1 |
день. Далее запустим ин- |
|||||||
|
|
|
|
|
|
струмент «Регрессия» |
пакета анализа. |
|
|||||||
|
|
|
|
|
|
|
В качестве объясняющей переменной в |
||||||||
|
|
|
|
|
|
этой модели выступают значения переменной y в |
|||||||||
|
|
|
|
|
|
предшествовавший момент времени |
t − 1 . По- |
||||||||
|
|
|
|
|
|
этому в поле «Входной интервал X» диалогового |
|||||||||
|
|
|
|
|
|
окна инструмента «Регрессия» зададим ячейки |
|||||||||
|
|
|
|
|
|
C3:C23, а в поле «Входной интервал Y» - ячейки |
|||||||||
|
|
|
|
|
|
B3:B23. Желательно поставить галочку в поле |
|||||||||
|
|
|
|
|
|
«Остатки» |
для расчета предсказанных значений |
||||||||
|
|
|
|
|
|
объясняемой переменной. |
|
|
|
||||||
|
|
|
|
|
|
|
Расчеты дают следующую модель (см. в |
||||||||
|
|
|
|
|
|
таблицах вывода итогов): |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
ˆyt =126,986 +0,903 yt −1 . |
|
|||||
|
|
|
|
|
|
|
Корреляционная |
связь |
между |
yt и yt −1 |
|||||
|
|
|
|
|
|
тесная ( r =0 ,929 ). Качество |
модели |
довольно |
|||||||
|
|
|
|
|
|
высокое ( R |
|
|
0 ,862 , |
R |
|
0 ,855 ). Средняя отно- |
|||
|
Рис. 5.22 |
|
|
|
|
|
2 |
= |
|
ˆ |
2 = |
|
|
|
|
127
Полянский Ю.Н. Эконометрика. Экономическое моделирование и прогнозирование.
сительная ошибка очень мала ( A =2 ,86% ). Полученная модель значима в целом ( F = 118,88 > F0 ,05 ;1;19 = 4 ,38 ) и значим её коэффициент регрессии b1
|
|
= 10 ,9 > t0 ,95 ;19 = 2 ,09 ). |
|
|
|
|
|
|
|
|
|
|
||||||||||
( |
tb |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученная авторегрессионная модель AR(1) в данном случае гораздо |
||||||||||||||||||
более точна и значима, |
чем классическая модель парной линейной регрес- |
|||||||||||||||||||||
сии, |
полученная сначала. Это хорошо видно и на графике регрессионной за- |
|||||||||||||||||||||
висимости |
yt |
на |
yt −1 |
(рис.5.23). Точки расположены гораздо ближе к линии |
||||||||||||||||||
регрессии и отсутствует положительная автокорреляция. |
||||||||||||||||||||||
|
|
|
|
Точечный прогноз курса акций на момент времени t =23 : |
||||||||||||||||||
|
|
|
|
ˆ |
= |
126,986 |
+ |
0,903 y22 |
= |
126,986 |
+ |
0,903 |
|
1279 |
= |
1281,42 (руб.). |
||||||
|
|
|
|
y23 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
Как видим, он существенно отличается от полученного ранее по клас- |
||||||||||||||||||
сической парной линейной модели. |
Там он был получен на продолжении |
|||||||||||||||||||||
прямой линии регрессии, т.е. |
только с учетом тренда. |
А здесь – учитывает |
||||||||||||||||||||
ещё и периодические колебания временного ряда. |
|
|
||||||||||||||||||||
|
|
|
|
3) В некоторых случаях более точной может оказаться авторегресси- |
||||||||||||||||||
онная модель 2-го порядка |
AR(2). Поэтому попробуем её построить. Учтём |
|||||||||||||||||||||
в модели значения курса акций не только в предшествовавшие моменты |
||||||||||||||||||||||
времени |
t − 1 , но и за 2 |
дня до текущего. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
Добавим |
|
в |
|
таблицу |
|
|
|
|
|
|
|
|
|
|||||
столбец |
D, |
назвав |
его |
«y(t- |
|
|
|
|
|
|
|
|
|
|||||||||
2)». |
|
В нём будут данные из |
|
|
|
|
|
|
|
|
|
|||||||||||
столбца |
B, |
сдвинутые на |
2 |
|
|
|
|
|
|
|
|
|
||||||||||
дня вперед. |
Скопируем дан- |
|
|
|
|
|
|
|
|
|
||||||||||||
ные из ячеек |
B2:B21 |
в |
ячей- |
|
|
|
|
|
|
|
|
|
||||||||||
ки |
D4:D23 (рис. 5.22). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Опять с помощью па- |
|
|
|
|
|
|
|
|
|
|||||||||
кета анализа получим табли- |
|
|
|
|
|
|
|
|
|
|||||||||||||
цу вывода итогов. |
Для этого |
|
|
|
|
|
|
|
|
|
||||||||||||
в поле «Входной интервал |
X» |
|
|
|
|
|
|
|
|
|
||||||||||||
диалогового окна инструмен- |
|
|
|
|
|
|
|
|
|
|||||||||||||
та |
«Регрессия» |
зададим ячей- |
|
|
|
|
|
|
|
|
|
|||||||||||
ки |
C4:D23 (т.е. |
массив значе- |
|
|
|
|
|
|
|
|
|
|||||||||||
ний |
yt −1 |
и |
|
yt −2 |
в моменты |
|
|
|
|
|
|
|
|
|
||||||||
t =3,4 ,...,22 ), |
|
а |
в |
поле |
|
|
|
|
|
|
Рис. 5.23 |
|||||||||||
«Входной |
интервал |
|
Y» |
- |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ячейки B4:B23 (т.е. |
yt в те же моменты времени). |
|
|
|||||||||||||||||||
|
|
|
|
Расчеты дают модель |
|
|
|
|
|
|
|
|
|
|
||||||||
ˆyt = 101,25 + 1,223 yt −1 − 0,304 yt −2 .
128

Полянский Ю.Н.
Эконометрика. Экономическое моделирование и прогнозирование.
Её показатели качества и значимости:
|
|
r =0 |
,941 , |
R |
2 |
=0 ,886 |
ˆ |
2 |
=0 ,872 , |
|||||
|
|
|
, R |
|
|
|||||||||
|
|
F = 65 ,81 > F0 ,05 ;1 ;18 |
= 4 ,41 , |
|
=2 ,63%, |
|||||||||
|
A |
|||||||||||||
tb |
|
= 5 ,59 > t |
0 ,95 ;18 |
= 2 ,10 , |
|
tb |
|
=1,42 <t0 ,95 ;18 =2 ,10 . |
||||||
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Введение в модель переменной yt −2 повысило точность и значимость модели в целом и несколько снизило значимость коэффициента b1 . Однако b1 остался значимым на выбранном уровне, а b2 оказался незначим (хоть и вблизи порога значимости). Недостаточная значимость b2 может объяс- няться тем, что с введением переменных в авторегрессионную модель при
неизменном количестве исходных данных постепенно уменьшается объем выборки.
Экономические соображения подсказывают, что на курс акций сего- дня влияет не только их курс вчера, но и позавчера (хоть и в меньшей сте- пени). Поэтому, вероятно, учет переменной yt 2 желателен. Но в таком слу- чае необходимы и дополнительные данные за период− времени до 1 апреля.
Получим прогноз по AR(2):
ˆy23 = 101,25+1,223y22 −0,304y21 = 101,25+1,223 1279−0,304 1283= 1275,30 руб.
Кстати, дальнейшее построение авторегрессионных моделей 3-го и 4- го порядков показывает, что с введением дополнительных переменных yt −3 и yt −4 показатели качества моделей постепенно растут, средняя относитель- ная ошибка ещё уменьшается, значимость моделей в целом снижается (но остается приемлемой). Однако низкими остаются показатели значимости коэффициентов регрессии.
4) Какая же модель более предпочтительна?
Классическая модель парной линейной регрессии в данном случае не желательна.
Если нет доступных данных о курсе акций до анализируемого периода (до 1-го апреля), то наиболее предпочтительна для прогноза в данной задаче авторегрессионная модель 1-го порядка AR(1).
Если такие данные есть, то можно продолжить исследования. Вполне возможно, что авторегрессионные модели более высокого по- рядка могут оказаться более предпочтительными.
129
