16. Нелинейные преобразования ГО (операции композиции, декомпозиции и мультиплицирования).
1. Композиция - объединение более мелких объектов в один. Необходимо задать правила вычисления атрибутов аналогичных данных для создаваемого нового объекта. В процессе обобщения вычисляются данные для создающегося объекта в зависимости от заданного метода отношений атрибутов. Большинство ГИСтехнологий содержит следующие методы обобщения данных при объединении объектов:
•сумма - значения атрибутов, соответствующих исходным объектам , складываются, и сумма присваивается новому объекту. At{M) =T.At(A.)i I.......k (где k - число исходных объектов)
•среднее - вычисляется среднее значение атрибутов исходных объектов и присваивается атрибуту нового объекту. At{M) = T.At{A,)l кi=l.......k
•взвешенное среднее - разные значения для исходных объектов умножаются на различные коэффициенты (веса) р Веса можно
брать из любого числового поля таблицы или вычислять по значению характеристики пространственного объекта (например, использовать его площадь или периметр, которые могут отсутствовать в таблице.)
2. Декомпозиция (break) – обратная композиция. При декомпозиции используют следующие методы преобразования атрибутов:
•пусто - удаляет значение, которое соответствовало изменяемому объекту.
•значение - сохраняет значение, которое соответствовало изменяемому объекту.
•пропорционально размеру - вычитает из значения (которое соответствовало изменяемому объекту) долю, пропорциональную размеру вырезанного фрагмента.
3. Мультиплицирование - преобразование отдельного изображения в большое число идентичных изображений. Методы:
•Шаговые фотокамеры с последовательным экспонированием - создает последовательно одно изображение за другим,
причем их местоположением можно управлять. Преимущества такого прибора заключаются в доступности, легкости программирования, идентичности качества каждого изображения и разнообразии вариантов.
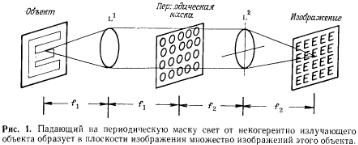
•Некогерентные оптические системы (рис 1) - При
точечном освещающем источнике в выходной плоскости |
|
формируется изображение периодической маски (ПМ). Если |
|
освещающим источником является входное изображение, то |
на |
выходе наблюдается множество копий входного изображения |
— |
по одному изображению для каждой точки периодической |
|
маски. |
|
•Когерентные неголографические системы;
•Когерентные голографические системы.
Встрого когерентных вариантах системы периодическая структура осуществляет выборку дифракционной картины Фраунгофера входного изображения, так что выходное изображение представляет собой свертку входного изображения с периодической функцией.
Этим двум методам присущи два основных недостатка. Во-первых, в выходном изображении имеет место конкуренция между яркостью и разрешением. Чтобы получить хорошее разрешение, маска должна иметь очень маленькие отверстия, а чтобы иметь хорошее пропускание, отверстия должны быть большие. Во-вторых, очень трудно получить N изображений с одинаковой яркостью. Эти проблемы голографического мультиплицирования изображений требуют своего решения.
17. Операция отсечения ГО (алгоритм Сазерленда)
Преобразование отсечения
Рассмотрим команду построения линии в AutoCad:
Command: line
from point 0,0
to point 2000,1500
y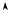 
600
Для этого отрезка необходимо выполнить scan-преобразование x
(0;0) |
800 |
Отсечение- это отбрасывание части изображения, лежащей вне заданной области (вне заданного окна).
В приведённом примере: чтобы выполнить отсечение отрезка, ограниченного прямоугольным окном отсечения, необходимо исследовать уравнение отрезка для каждой границы области отсечения:
форма окна более сложная, то расчёты ещё более усложняются.
Общее требование - окно отсечения должно быть выпуклым.
Выпуклая |
Не выпуклая |
|
фигура: |
||
примеры выпуклых |
фигура |
|
фигур: |
||
|
||
> квадрат; |
(вогнутая - ?) |
|
|
Алгоритм Сазерленда
В этом алгоритме отсутствует вычисление точек пересечения с окном. Окно отображения делит экран на 9 областей, положение в которых задаётся четырёхразрядным двоичным кодом.
Область окна отсчёта изображения кодируется четырёхразрядным двоичным кодом (в данном случае, a0 - старший разряд):
Область изображения |
a0 |
a1 |
a2 |
a3 |
Область окна отсечения |
0 |
0 |
0 |
0 |
Область выше окна отсечения |
1 |
X |
X |
X |
Область ниже окна отсечения |
X |
1 |
X |
X |
Область, правее окна отсечения |
X |
X |
1 |
X |
Область, левее окна отсечения |
X |
X |
X |
1 |
Например, в разряде a0 стоит 1, если область находится выше окна отсечения.
Рассматривается несколько случаев:
1)отрезок целиком находится в области окна отображения;
2)отрезок частично находится в области окна отображения;
3)отрезок не находится в области окна отображения.
Всем точкам, формирующим изображение (началам и концам отрезков) присваиваются коды областей, где они расположены.
Алгоритм:
1) Определяется, лежит ли отрезок полностью в области отсечения. Для этого выполняется операция логического "ИЛИ" кодов конца отрезка. И если результат =0, то отрезок полностью лежит в области окра отсечения и должен быть сохранён;
2) я ли отрезок полностью вне окна отсечения. Для этого выполняется операция логического "И". Если результат операции НЕ равен нулю, то этот отрезок лежит вне области окна отсечения и должен быть отброшен; 3) Если логическое "ИЛИ" для кодов конца отрезка НЕ равно 0, а логическое "И" равно =0, то отрезок прямой пересекается с
окном отображения. Причём, результат логического "ИЛИ" (не равный нулю) укажет, с какой границы от окна отображения находится отрезок;
4)Далее, если отрезок пересекает окно отображения, ищем точку пересечения; и концам отрезков присваиваются новые
коды;
5)Далее алгоритм повторяется для полученных отрезков.
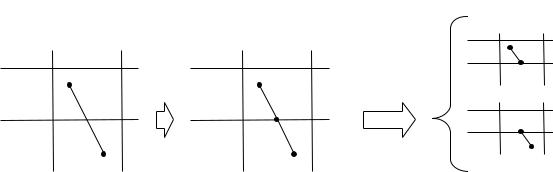
Если отрезок частично |
Отрезок разбивается на |
|
|
|
|
|||||
находится в области |
части - в месте |
Алгоритм |
|
|
||||||
отображения |
пересечения с окном |
повторяется для |
|
|
|
|||||
|
|
|
||||||||
|
|
|||||||||
|
|
|
|
|
|
|
каждого из |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
полученных |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
отрезков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3 применяется алгоритм нахождения пересечения отрезка с границей области отсечения.
18. Растровые преобразования прямой (СКЭН преобразования).
Рассмотрим команду построения линии в AutoCad:
Command: line
from point 5,10
to point 10,20
К (конец) |
(10,20) |
(5,10) |
Н (начало) |
Цель scan-преобразования - представить начальную и конечную координату отрезка в совокупность пикселей в видеобуфере.
Подходы к решению задачи:
1) Использование классического уравнения прямой.
y = Ax + B
x1 ≤ xi ≤ x2
yi = Ax + B; A = tgα,т.е.
yi+1 = A(xi +∆) + B = Axi + B + ∆A = yi + ∆A
т.е. перебираем все множество точек. Чем меньше зерно (пиксель), тем дольше идет операция. Занимает много времени, а следовательно уменьшается быстродействие. Такой подход редко используется, несмотря на простоту.
2) Метод вычисления по приращению (алгоритм Брезенхема1)
По известным координатам x и y начального пикселя прямой с помощью прибавления приращений по осямx и y с учётом наклона прямой можно найти положение следующего пикселя.
С помощью этого алгоритма формируется набор пикселей, наиболее близко прилежащих к данной прямой.
Допущения:
1.Наша прямая проходит через начало координат;
2.Она проходит под углом α ≤ 45° (0 ≤ tgα ≤ 1);
3.x2 > x1 ;
4.(0, 0) – координаты начального пикселя.
Тогда уравнение прямой:
y = |
y2 − y1 |
x = dy x |
||
|
||||
|
x |
2 |
−x |
dx |
|
|
1 |
|
|
То есть в общем случае мы имеем алгоритм следующего вида:
Начало алгоритма
|
|
α |
|
3 |
|
|
|
|
1 |
1 |
2 |
3 |
4 |
|
0<α<45 |
-45<α<0 |
45<α<90 |
-90<α<-45 |
2 |
|
|
|
|
4 |