39 Обращения преобразования Лапласа. Достаточные условия существования оригинала.

Теорема

Если функция 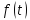является оригиналом аее изображением тоудовлетворяет условиям Гельдера справедливо равенствогде интеграл берётся по любой прямойи понимается в смысле главного значения.

Док-во

Рассмотрим интеграл Осталось показать чтоI(b)=

I(b)=здесь 2 и 3 слагаемые сходящиеся интегралы поэтомучто каждый из этих интегралов по модулю меньше(по Лемме Римана первое слагаемое, итак

Следствие (Теорема единственности)

Оригинал восстанавливается по своему изображениюоднозначно во всех точках , удовлетворяющих условию Гельдера, значение оригинала в точках разрыва не влияют на изображение.

Теорема (достаточные условия существования оригинала)

Пусть функция пусть приабсолютно сходится, тогдаявляется отображением функции. (без док-ва)

40. Общие свойства преобразования Лапласа (линейность, правила подобия, дифференцирования, смещения, интегрирования).

1. Линейность

Пример:

;

;

;;

2. Теорема подобия

Для действительно

3. Дифференцирование интеграла

–непрерывно кусочно-дифф. при – оригинал, то

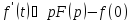
, где

4. Дифференцирование изображения

Д-но, дифф. по переменной р равенстваполучим

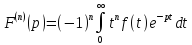
Пример:

, ,,.

5. Интегрирование оригинала

Если , тодействительноочевидно явл-ся оригиналом, причем, положим.

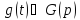6. Интегрирование изображения

и интеграл– сходится, то,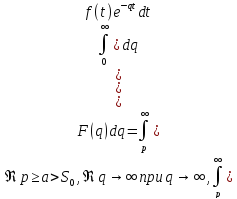Так какоткуда след. равн. сх-ть относит.qв (4).

7. Теорема запаздывания

8. Теорема смещения

Для .Пример:,

41.Свёртка оригиналов и её изображение.

Опр.Сверткой функцийназывается функция.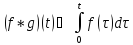

Лемма. Пустьфункция двух действительных переменныхабсолютно сходится в пл.и сущ. повторный интегралтогда.

Теорема умножения.Произведение двух изображенийтакже явл-ся изображением, причем

Интеграл Дюамеля.

42. Теоремы разложения.

Теор1. Если функцияголоморфна в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд имеет вид,то (2) оригинал с разложениемF(p).

Теор2. ПустьF(p) :

1. Голоморфна всюду, за исключением конечного числа особых точек лежащих в конечной плоскости.

2. 

3. абсолютно сходится тогда

Док-во: Применим теор. , согласно которойобозначим меруконтур, составленный из частилежащей слева от прямойи отрезка этой прямой, соединяющего концы дуги. По лемме Жордана приt>0, поэтому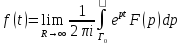. Применяя т. Коши о вычетах, получим (7).

След.Если функция, то ее оригиналполюсы фун.F(p).

Если полюсы простые, то .

43. Дискретное преобразование Лапласа. Z-преобразование.

Опр. Z- преобразованием числовой бесконечной посл-тиназывается функцияF(z) компл. Переменнойz, определяемая прирядом Лорана:и аналитически продолженная в круг |z|<R.

43. Применение операционного исчисления к решению дифференциальных уравнений.

Для того чтобы найти x(t) линейного д.у. с постоянными коэфф., удовлетворяющее начальным условиям:следует применить к обоим частям ур-ия преобразования Лапласа:

L(p)X(p)+Q(p)=F(p), где,

Найдя оригинал для X(p), получим исходноеx(t). Аналогично решаются системы.

Пример:

,;

;

;

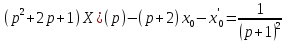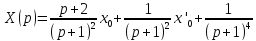Пользуясь таблицей, находим: , где;

Частное решение, удовл. начальным условиям: .

N

f(t)

F(p)

N

f(t)

F(p)

1

 (t)

1/p

6

sint



p22

2

t n

1/p n1

7

cht

p

p 22

n!

3

et

1/ ( p )

8

sht



p 22

4

t n

1

9

etcost

p 

et

( p )n1

( p ) 22

n!

5

cost

p

10

etsint



p 22

( p ) 22