36 Аналитическое продолжение по цепи областей.

Пусть Ḋ ϲf–голоморфная функция в Ḋ . Совокупность Ḋ и f называется элементами и обозначается {Ḋ,f} при этом Ḋназывают областью элемента. Элемент {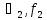} называют непосредственным аналитическим продолжение элемента {} если:d: =является областью и. Из принципа единственности следует что. Таким образом, если элемент {} является непосредственным аналитическим продолжением {} то это продолжение единственно . Оно обратимо {} является непосредственным аналитическим продолжением {}. Конечное множество элементов {},…, {} – называется цепью если элемент {} является непосредственным аналитическим продолжение элемента {} (k=1,2,3,4,5….,m) При этом говорят что элемент {} является аналитическим продолжением элемента {} по соединяющей их цепи области.

37 Принцип симметрии Римана-Шварца.

Пусть две непересекающиеся области имеют общий участок границы, содержащий кусочно-гладкую простую дугубез ее конечных точек. Рассмотрим множество=– приставляющее собой область.

Лемма

Пусть функция (k=1,2…) голоморфна в области(и непрерывна наЕслиzто функцияравнаяи равная на, общее значение является голоморфным в.

Это лемма будет исполняться в том частном случае когда интеграл по прямой, но в этом случае ее справедливость следует из замечания к теореме Мореры.(без доказательства)

Теорема (принцип симметрии Римана-Шварца)

Если функция f голоморфна в и непрерывна ви в точке интегралапринимает значения принадлежащие интегралунекоторой прямойTто функция f аналитически продолжается из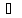в областьпричем значенияприzсимметричны со значениямиотносительногде=zточка симметричнаяW=zотносительно Г, то функция.

Доказательство

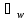Повернем плоскости илинейным преобразованиемz=az+bw=выбрав их так чтобы интегралв некоторый интеграл действительной оси плоскости. А примая Г перешла в действительную ось плоскости. Эти преобразования сохранили симметрию точек относительно преобразования прямых а также сохранили непрерывность и голоморфность , далее считаем чтоиинтегралы действительной оси плоскостиисоответственно в окрестностиU()вфункцияfпредставляется степенным рядом.

Определим в области .

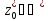Показав что голоморфна в окрестностиU() тсимметрична точке. В силу непрерывностиfви того чтоfна.

Теперь легко видеть что z. Согласно лемме функцияголоморфна в области. В этой областиусловиючто означает симметрию относительно Г точекzисимметричных относительно.

38Понятие функции-оригинала. Показатель роста оригинала. Изображение по Лапласу, голоморфность изображения.

Функцией-оригиналом называется любая комплексная функция 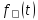действительного переменногоtудовлетворяющая следующим условиям.

1. Функция удовлетворяет условиям Гельдера всюду на осиtкроме отдельных точек, где она имеет разрывы первого порядка , причем на каждом конечном интервала таких точек конечное число, это означает что для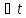кроме точек разрыватакие что(1)

2. 

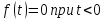
3. Существуют такие постоянные (2)

Определение

Нижняя грань Sпри которой неравенство (2) выполняется с некоторыми постоянными.

Замечание

Из определения следует что то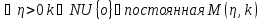такая что|

Определение

Изображение функции-оригинала (по Лапласу) называется функциякомплексного переменногоопределённая равенством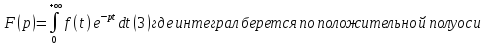Здесь само преобразованиеназывается преобразованием Лапласа. Функцияимеет своим изображением функциюзаписываютили

Теорема

Для всякого оригинала изображениеопределено в полуплоскостигде- показатель роста функции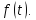И является в этой плоскости голоморфной функцией при этом(4)

Док-во

Пусть имеем|=(5);Интеграл (3) сходится абсолютно в полуплоскостии определена функциядокажем ее голоморфность в этой полуплоскости. Фиксируемположим= -(6) оценимОтсюда и из (6) получим