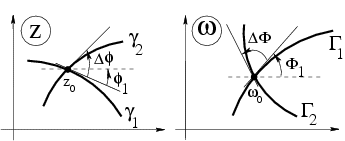- •6. Определение и общие свойства линейного и дробно-линейного отображения.
- •7. Круговое свойство дробно-линейного отображения, свойство сохранения симметрии, инвариантность ангармонического отношения.
- •10. Интеграл от функции комплексного переменного вдоль кривой. Вычисление интеграла. Интеграл вдоль окружности от функции Zk, k ϵ z. Свойства интеграла
- •12. Обобщение интегральной теоремы Коши на случай, когда функция не является голоморфной на контуре интегрирования
- •13 Интегральная формула Коши. Теорема о среднем
- •14. Теорема Тейлора о разложении голоморфной функции в степенной ряд. Следствия: существование у голоморфной функции производных всех порядков, интегральная формула для производных.
- •15. Неравенства Коши для коэффициентов степенного ряда и теорема Лиувилля. Основная теорема алгебры.
- •16. Теорема о существовании первообразной у голоморфной функции. Формула Ньютона-Лейбница.
- •17. Гармонические функции. Восстановление голоморфной функции по её действительной части. Сопряжённые гармонические функции. Бесконечная дифференцируемость гармонических функций.
- •18. Теорема Мореры.
- •21. Принцип максимума модуля.
- •27.Понятие вычета голоморфной функции относительно изолированной особой точки. Приёмы вычисления вычетов.
- •28. Теоремы Коши о вычетах
- •29. Интеграл от логарифмической производной. Принцип аргумента.
- •30.Теор Руше.
- •31.Принцип сохранения области
- •32. Лемма об интегралах по дугам окружностей. Вычисление несобственных интегралов вида.
- •33. Лемма Жордана. Вычисление интегралов вида.
- •34. Интегралы в смысле главного значения и их вычисление.
- •35. Целые и мероморные функции. Представление рациональной функции в виде суммы многочлена и простейших дробей.
- •36 Аналитическое продолжение по цепи областей.
- •37 Принцип симметрии Римана-Шварца.
- •38Понятие функции-оригинала. Показатель роста оригинала. Изображение по Лапласу, голоморфность изображения.
- •39 Обращения преобразования Лапласа. Достаточные условия существования оригинала.
- •40. Общие свойства преобразования Лапласа (линейность, правила подобия, дифференцирования, смещения, интегрирования).
- •41.Свёртка оригиналов и её изображение.
- •42. Теоремы разложения.
(1)Показательная функция, теорема сложения показателей. Тригонометрические функции sin(z) и cos(z), формулы Эйлера, теорема сложения для функций sin(z) и cos(z), нули функций sin(z) и cos(z). Гиперболические функции и их связь с тригонометрическими функциями.
Опр:Сумму степенного ряда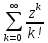 , сходящуюся на всей плоскостити
, сходящуюся на всей плоскостити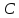 , обозначают через
, обозначают через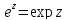 и называют показательной (экспаненциальной)
ф-цией:
и называют показательной (экспаненциальной)
ф-цией: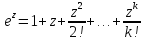 (1)
(1)
Теорема сложения показателей(для экспоненциальной ф-ции):
Для
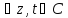 имеем
имеем (2)
(2)
Док-тво:
По опр. произведение этих рядов
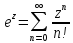 ,
,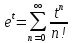 есть ряд
есть ряд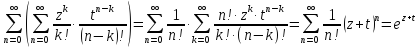
Отсюда и из теоремы о произведении рядов
(произведение абсолютно сходящихся
рядов явл. абсолютно сходящимся рядом,
сумма которого равна произведению сумм
перемножаемых рядов)
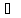 доказываемое
доказываемое
Следствие:
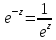 ,
,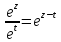
Для
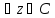 :
:
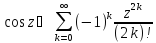 (3)
(3)
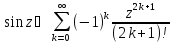 (4)
(4)
Из (1), (3) и (4)
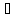 формула Эйлера:
формула Эйлера: (5)
(5)
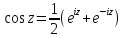 (6)
(6)
 (7)
(7)
Из (2) и (5)

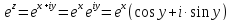 (8)
(8)
Поскольку при
 то
то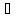 ф-ция
ф-ция плоскости
плоскости в нуль не обращается. Пользуясь ф-лой
Эйлера, тригонометрическая запись
комплексного числа
в нуль не обращается. Пользуясь ф-лой
Эйлера, тригонометрическая запись
комплексного числа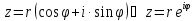
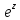 явл. периодической ф-цией с периодом
явл. периодической ф-цией с периодом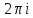 :
: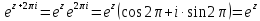
Теорема о сложении ф-ций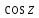 и
и :
:
Для
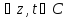 имеем:
имеем: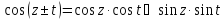 ,
,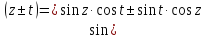
Следствие: 1) число
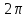 есть период для
есть период для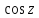 и
и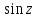 комплексной плоскости (
комплексной плоскости ( из теоремы о сложении ф-ций
из теоремы о сложении ф-ций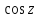 и
и при
при );
2)
);
2) (
(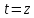 )
)
Утв:1) нули ф-ции имеют вид
имеют вид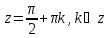 , 2) нули ф-ции
, 2) нули ф-ции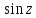 имеют вид
имеют вид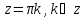
Док-тво:
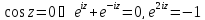 полагая
полагая находим
находим
Аналогично находятся нули
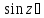
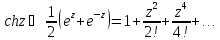
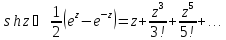
Сравнивая с (6) и (7) получим:
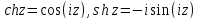
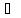

(2)Производная функции комплексного переменного. Критерий существования производной. Формулы для производной.
Пусть
в обл.
 задана однозначно ф-ция
задана однозначно ф-ция ,
точка
,
точка
Опр:если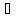 конечный предел
конечный предел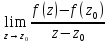 , то он называется производной от ф-ции
, то он называется производной от ф-ции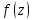 в точке
в точке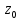 и обозначается
и обозначается ;
сама ф-ция
;
сама ф-ция при этом называется дифференцируемой
или моногенной в точке
при этом называется дифференцируемой
или моногенной в точке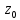
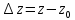 ,
,
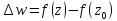
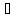 условие моногенности:
условие моногенности: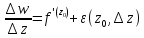 (1) , где
(1) , где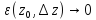 при
при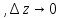
Отсюда
следует, что приращение
 моногенно в точке
моногенно в точке и может быть представимо в виде
и может быть представимо в виде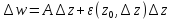
 (2) гдеAне зависит от
(2) гдеAне зависит от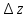 ,
а
,
а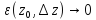 при
при
Из
(2)
 непрерывность моногенной в точке
непрерывность моногенной в точке ф-ции
ф-ции
Представимость
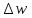 в виде
в виде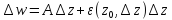
 , гдеAне зависит от
, гдеAне зависит от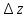 ,
а
,
а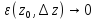 при
при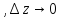 ,
является необходимым и достаточным
условием моногенности ф-ции.
,
является необходимым и достаточным
условием моногенности ф-ции.
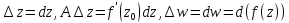 ,
,

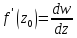
Теорема:
Для
того чтобы ф-ция
 ,
опр. в некоторой обл.G,
была моногенной в точке
,
опр. в некоторой обл.G,
была моногенной в точке этой
обл. необходимо и достаточно чтобы ф-ции
этой
обл. необходимо и достаточно чтобы ф-ции и
и были дифференцируемы в этой точке (как
ф-ции 2-х действительных переменных) и
чтобы, кроме того в точке
были дифференцируемы в этой точке (как
ф-ции 2-х действительных переменных) и
чтобы, кроме того в точке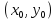 ,
выполнялись условия:
,
выполнялись условия: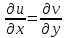 ,
, (3)
(3)
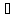
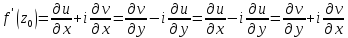 - формулы для производной
(4)
- формулы для производной
(4)
Док-тво:
Необходимость:
Если
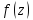 моногенна в точке
моногенна в точке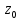 ,
то
,
то (5) где
(5) где

Отделяя
в (5) действ. и мнимую части получим:
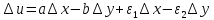 ,
,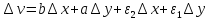 Отсюда и из того, что
Отсюда и из того, что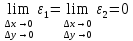
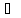 1) ф-ции
1) ф-ции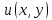 и
и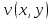 дифференцируемы в точке
дифференцируемы в точке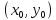 ;
2)
;
2)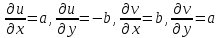 (6)
(6)
Из
(6)
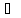 (3), т.к.
(3), т.к. из (6)
из (6) (4)
(4)
Достаточность:
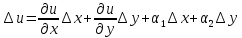 ,
,
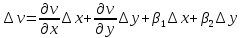 где
где
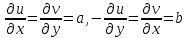
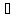
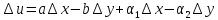 ,
,
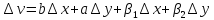
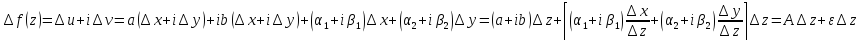 (7)
(7)
Т.к.
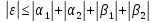 , то
, то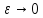 при
при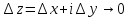 Отсюда и из (7)
Отсюда и из (7)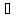


(3)Определение голоморфности функции в точке и на множестве.
Опр:ф-цияfназывается
голоморфной в точке ,
ести она моногенна в некоторой окрестности
этой точки.
,
ести она моногенна в некоторой окрестности
этой точки.
Говорят,
что ф-ция f(z)голоморфна в точке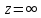 ,
если ф-ция
,
если ф-ция голоморфна в точкеz=0.
голоморфна в точкеz=0.
Опр:ф-цияfназывается голоморфной на множестве ( в частности, в области), если она голоморфна в каждой точке этого множества.
Исходя
из опр, отметим, что голоморфная ф-ция
в замыкании обл. G,
означает, что ф-ция голоморфна в некоторой
обл.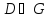 .
.
Наряду с термином «голоморфная ф-ция» используют также термины «аналитическая ф-ция» и «регулярная ф-ция». Эти термины тождественны.
(4)Теорема о голоморфности суммы степенного ряда. Следствия.
Теорема:сумма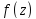 степенного ряда
степенного ряда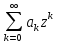 в круге сходимости
в круге сходимости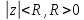 ,
является голоморфной ф-цией. При этом
,
является голоморфной ф-цией. При этом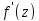 может быть получена путем почл.
дифференцирования ряда:
может быть получена путем почл.
дифференцирования ряда:
Док-тво:
известно, что радиус сходимости ряда
 (1) также равенR.
Пусть
(1) также равенR.
Пусть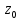 какая-либо точка круга
какая-либо точка круга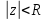 ,
возьмем
,
возьмем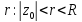 ,
из абсолютной сходимости ряда (1) в круге
,
из абсолютной сходимости ряда (1) в круге

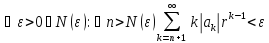 (2)
(2)
При
 имеем:
имеем:
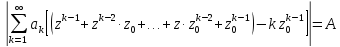
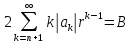
Слагаемое
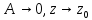 , поэтому оно меньше
, поэтому оно меньше
Слагаемое
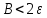

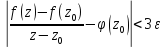
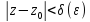

Применяя
теорему к сумме ряда
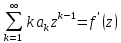 , получаем, что
, получаем, что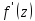 также явл. голоморфной ф-цией в круге
также явл. голоморфной ф-цией в круге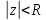 ,
причем
,
причем
Следствие:
1)
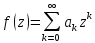 бесконечно дифф. в круге сходимости
бесконечно дифф. в круге сходимости
2)
каждый степенной ряд с положительным
радиусом сходимости явл. рядом Тейлора
для своей суммы (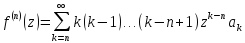 , положивz=0, получим
, положивz=0, получим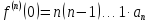
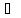
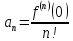
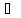
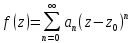 ,
,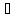
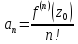 )
)
3)
пусть ряды
 имеют одну и ту же сумму
имеют одну и ту же сумму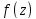 ,
в окрестности
,
в окрестности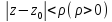 тогда
тогда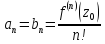 (это предложение выражает св-во
единственности разложения в степенной
ряд)
(это предложение выражает св-во
единственности разложения в степенной
ряд)
4)
если сумма
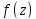 степенного ряда
степенного ряда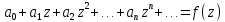 явл. четной ф-цией, то все коэффициенты
с нечетными индексами равны нулю и
наоборот
явл. четной ф-цией, то все коэффициенты
с нечетными индексами равны нулю и
наоборот
5)
 аналитичны всюду в плоскости
аналитичны всюду в плоскости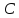 ,
при этом имеем:
,
при этом имеем: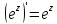 ,
,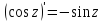 ,
,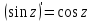 ,
, ,
,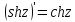
(5)Геометрический смысл аргумента и модуля производной. Понятие о конформном отображении.
Согласно определению производной функции комплексного переменного:
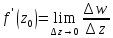
|
|
Рассмотрим
на плоскости
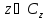 кривую
кривую ,
а также образ кривой
,
а также образ кривой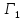 на
плоскости
на
плоскости .
Точке
.
Точке будет
соответствовать точка
будет
соответствовать точка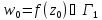 .
Если производную представить в виде
.
Если производную представить в виде ,
то аргумент производной
,
то аргумент производной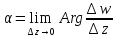
т.к.


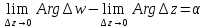 и, как следует из
рисунка
и, как следует из
рисунка
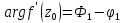 ;
;
таким образом, геометрический смысл аргумента производной состоит в том, что
 равен разности углов
касательных к кривой
равен разности углов
касательных к кривой
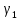 и
ее образу
и
ее образу в
точках, связанных условием
в
точках, связанных условием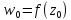 .
.
Рассматривая
две кривых
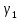 и
и
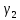 , а также их
образы
, а также их
образы
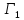 и
и
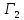 ,
легко показать, что
,
легко показать, что

т.
е. углы между кривыми на комплексной
плоскости и их образами в точке
 не изменяются
в случае, если
не изменяются
в случае, если
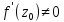 .
.
Такое свойство называется свойством сохранения углов.
Геометрический смысл модуля производной следует из соотношения:

которое означает,
что
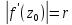 являетсякоэффициентом
растяжения в
точке
являетсякоэффициентом
растяжения в
точке
 при отображении
с помощью функции
при отображении
с помощью функции
 .
.
Если
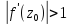 ,
то в окрестности точки
,
то в окрестности точки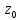 расстояния между
точками увеличиваются, при
расстояния между
точками увеличиваются, при
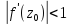 - сжимаются, но так как значение
- сжимаются, но так как значение по определению
не зависит от направления, по которому
по определению
не зависит от направления, по которому
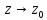 ,
то в окрестности
,
то в окрестности коэффициент
растяжения является постоянным.
коэффициент
растяжения является постоянным.
Опр:
голоморфное отображение обл.
 на обл.
на обл.
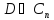 при котором для каждой т.
при котором для каждой т.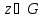 имеет место консерватизм углов и
постоянство растяжений, называется
конформным.
имеет место консерватизм углов и
постоянство растяжений, называется
конформным.
Теорема:
отображение, осуществляемое голоморфной
ф-цией
 ,
явл. конформным достаточно малой
окрестности каждой точкиz,
в которой
,
явл. конформным достаточно малой
окрестности каждой точкиz,
в которой
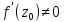
(док-тво какое-то хуевое)
Теорема:
если при отображении осуществл.
однозначной ф-цией
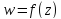 в каждой точке
в каждой точке имеет место консерватизм углов и
постоянство растяжения, то ф-ция
имеет место консерватизм углов и
постоянство растяжения, то ф-ция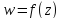 голоморфна в обл.G,
причем
голоморфна в обл.G,
причем
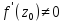 всюду в обл.G
всюду в обл.G
6. Определение и общие свойства линейного и дробно-линейного отображения.
Линейная функция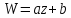
Отображение
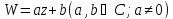 будет конформным во всей плоскости
будет конформным во всей плоскости

Функция

Соответствие,
даваемое этой формулой, взаимнооднозначно
во всех точках плоскости, причем в
нулевой точке z=0
(W=0)
соответствует бесконечно удаленная
точка W=∞
(z=0)
Полагая Рассмотрим
окружность
Рассмотрим
окружность Преобразовав
(1) удобно разбить на 2 более простых
Преобразовав
(1) удобно разбить на 2 более простых
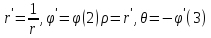 .
При
преобразовании (2) аргумент сохраняется,
а модуль изменяется на обратный. Точка
z,
находящаяся внутри окрестности C,
преобразуется в точку W’
, находящуюся вне окружности и лежащую
на продолжении отрезка Oz,причем
расстояние между 0, z
и W’
равно 1.
Такое отображение называется
инверсией
относительно окрестности C.
Точки z
и W’
при этом называются взаимно
симметричными
относительно окрестности C.
Отображение
(2) можно записать в виде:
.
При
преобразовании (2) аргумент сохраняется,
а модуль изменяется на обратный. Точка
z,
находящаяся внутри окрестности C,
преобразуется в точку W’
, находящуюся вне окружности и лежащую
на продолжении отрезка Oz,причем
расстояние между 0, z
и W’
равно 1.
Такое отображение называется
инверсией
относительно окрестности C.
Точки z
и W’
при этом называются взаимно
симметричными
относительно окрестности C.
Отображение
(2) можно записать в виде:
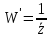 Преобразовав
(3):
Преобразовав
(3):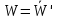 Совокупность
двух отображений дает голоморфное (z≠0)
отображение
Совокупность
двух отображений дает голоморфное (z≠0)
отображение
 Это
отображение будет сохранять углы во
всех плоскостях
Это
отображение будет сохранять углы во
всех плоскостях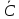 ,
включаяz=0,
z=∞
При
этом под углом двух линий при z=∞
понимают угол, образованныйотображениием
линиями посредством функции
,
включаяz=0,
z=∞
При
этом под углом двух линий при z=∞
понимают угол, образованныйотображениием
линиями посредством функции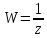 в плоскостиW
при W=0.
в плоскостиW
при W=0.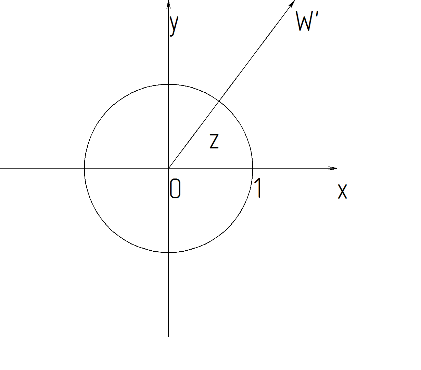

Дробно-линейная
функция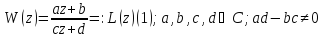 Обратно,
z
можно выразить через W:
Обратно,
z
можно выразить через W:
 Таким
образом, соответсвуют формулы (1) является
взаимно однозначным
точка
Таким
образом, соответсвуют формулы (1) является
взаимно однозначным
точка будет соответствоватьW=∞,
а точка
будет соответствоватьW=∞,
а точка
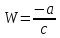 - точкаz=∞.
Функция
(1) сохраняет углы во всех точках
расширенной плоскости
- точкаz=∞.
Функция
(1) сохраняет углы во всех точках
расширенной плоскости
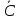
Теор:
Образом прямой или окружности при
отображении
 является прямая или окружность.
является прямая или окружность.
Док-во:
Для линейной функции
 это свойство является очевидным.
Расссмотрим
отображение
это свойство является очевидным.
Расссмотрим
отображение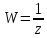 .
Уравнение окружности имеет вид:
.
Уравнение окружности имеет вид: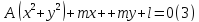 .
ПриA=0
уравнение (3) определяет прямую.
Перепишем
это уравнение в виде:
.
ПриA=0
уравнение (3) определяет прямую.
Перепишем
это уравнение в виде:
 ,
гдеAиC
– действительные постоянные,
,
гдеAиC
– действительные постоянные,
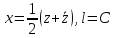 При
преобразовании
При
преобразовании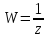 получаем
получаем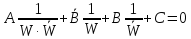 ,
или приведя к общему знаменателю, находим
,
или приведя к общему знаменателю, находим Уравнение
(4) определяет окружность плоскостиW
(приC=0
оно предстанляет прямую)
Поскольку
преобразование
Уравнение
(4) определяет окружность плоскостиW
(приC=0
оно предстанляет прямую)
Поскольку
преобразование
 представляет собой комбинацию
преобразований, для которых круговое
свойство выполняется, то теорема
доказана.
представляет собой комбинацию
преобразований, для которых круговое
свойство выполняется, то теорема
доказана.
7. Круговое свойство дробно-линейного отображения, свойство сохранения симметрии, инвариантность ангармонического отношения.
Дробно-линейное
отображение
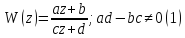 Зависит
от трех параметров, за которые могут
принять, например, отношение чисел a,
b,
c,
dк
одному из них.
Эти параметры однозначно
определяется из требований, чтобы три
заданных точки z1
, z2
, z3
плоскости
Зависит
от трех параметров, за которые могут
принять, например, отношение чисел a,
b,
c,
dк
одному из них.
Эти параметры однозначно
определяется из требований, чтобы три
заданных точки z1
, z2
, z3
плоскости
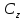 переходит
в заданные точкиW1
, W2
, W3
плоскости
переходит
в заданные точкиW1
, W2
, W3
плоскости
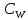 :
: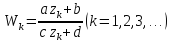 Чтобы
исключитьa,
b,
c,
d
из этих уравнений и из уравнения
Чтобы
исключитьa,
b,
c,
d
из этих уравнений и из уравнения
 образуем разности:
образуем разности: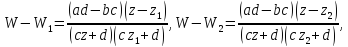
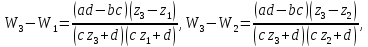 Отсюда
получим
Отсюда
получим
 Разрешаем
(2) относительно W,
получим искомое дробно-линейное
отображение. Оно переводит точки z1
,z2
, z3и
окрестность
Разрешаем
(2) относительно W,
получим искомое дробно-линейное
отображение. Оно переводит точки z1
,z2
, z3и
окрестность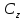 соответственно
в три точкиW1
, W2
, W3и
проходят через них окрестность
соответственно
в три точкиW1
, W2
, W3и
проходят через них окрестность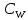 Тройки
точекz1
, z2
, z3и
W1
, W2
, W3
определяют направление обхода на
Тройки
точекz1
, z2
, z3и
W1
, W2
, W3
определяют направление обхода на
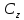 и
и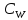 соответственно, причем области остающиеся
при этих обходах слева (справа)
соответствуют друг-другу при отображении
(2). Это является непосредственным
следствием конформности дробно-линейного
отображения.
соответственно, причем области остающиеся
при этих обходах слева (справа)
соответствуют друг-другу при отображении
(2). Это является непосредственным
следствием конформности дробно-линейного
отображения.
Отсюда
принимаем во внимание, что при отображении
(1) в случае действительных a,
b,
c,
d
Действительная ось ImZ=0
переходит в действительную ось ImW=0
и при ImZ=0
знак
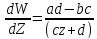 совпадает со знаком ad-bc. Получим следующие
утверждения
совпадает со знаком ad-bc. Получим следующие
утверждения
Теор1: При невырожденном дробно-линейном отображении (1) с действительными коэффицентами верхняя полуплоскость ImZ>0 переходит в верхнюю полуплоскость ImW>0, если ad-bc>0 и нижнюю, если ad-bc<0
Опр:Выражение
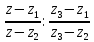 называется двойным. Равенство (2)
означает инвариантность ангармонического
отношения четырех точек при невырожденном
дробно-линейном отображением
называется двойным. Равенство (2)
означает инвариантность ангармонического
отношения четырех точек при невырожденном
дробно-линейном отображением
Теор2:
(свойство сохранения симметрии) Если
точки z1
,z2симметричны
относительно некоторой прямой или
окружности при дробно-линейном
отображении их
образы будут симметричны относительно
образовγ:
их
образы будут симметричны относительно
образовγ:
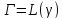
8. Степенная
функция W
= Zn.
Риманова поверхность функции Z=
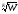 .
.
ФункцияW=Zn
однозначна и непрерывана на всей
плоскости
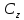 .
При n=1
она тождественно отображает
.
При n=1
она тождественно отображает
 на
на .
При отображенииW=Znкаждый
луч
.
При отображенииW=Znкаждый
луч переводит в луч
переводит в луч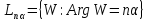 и, следовательно, углы с вершиной в точкеz=0
увеличиваются в n
раз. Точки
z1
,z2,
у которых модули равны, а аргументы
отличаются на величину, кратную
2π/nотображающ
в одну точку, в силу чего Zn
(n≥2)
в
и, следовательно, углы с вершиной в точкеz=0
увеличиваются в n
раз. Точки
z1
,z2,
у которых модули равны, а аргументы
отличаются на величину, кратную
2π/nотображающ
в одну точку, в силу чего Zn
(n≥2)
в
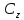 неоднолистна.
неоднолистна.
Однако на каждом множестве, не содержащих равных по модулю точек, с равными по модулю 2π/n аргументами, функция Znоднолистна.
Примерами таких
множеств служат углы
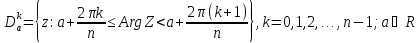 В
частности
В
частности
 исключив из него луч
исключив из него луч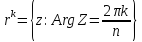 ,
получив область
,
получив область , которая однолистно отображается
функциейZn
на область
, которая однолистно отображается
функциейZn
на область
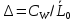 В
этой области однозначной является
функция
В
этой области однозначной является
функция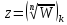 – ветви функции
– ветви функции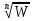 – обратной к функцииW=Zn
и называемой корнем n-ной
степени.
В области ∆
она является аналитической функцией,
причем
– обратной к функцииW=Zn
и называемой корнем n-ной
степени.
В области ∆
она является аналитической функцией,
причем Значение
Значение
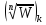 при
при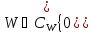 принадлежат
принадлежат
Пусть
 и значение
и значение Переместим
точкуW
от W0по
окружности |W
|=|W0|,
описывая при этом полную окружность.
Тогда ArgW
непрерывно возрастет на 2π,
а
Переместим
точкуW
от W0по
окружности |W
|=|W0|,
описывая при этом полную окружность.
Тогда ArgW
непрерывно возрастет на 2π,
а
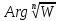 возрастет на 2π/n
⇒после обхода окрестности переходим
к значению
возрастет на 2π/n
⇒после обхода окрестности переходим
к значению
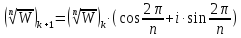 Послеn-кратного
обхода окрестности в одном направлении
получим
Послеn-кратного
обхода окрестности в одном направлении
получим
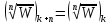 ,
т.е. указанные ветви функции
,
т.е. указанные ветви функции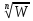 совпадают.
совпадают.
Рассмотрим
n
экземпляров области
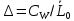 , которые обозначим ∆0,∆1,
… , ∆n-1Наложим
эти области одна на другую и склеим
нижний край разреза
, которые обозначим ∆0,∆1,
… , ∆n-1Наложим
эти области одна на другую и склеим
нижний край разреза
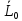 листа ∆k
(k=0,1,2,…,n-2)с
верхним краем такого же разреза листа
∆k+1
Свободный верхний край разреза L0
листа ∆0
склеим с нижним краем разреза ∆n+1
Если
точка М
– внутренняя для листа ∆k
(∆k+1),
то у нее существует ε окрестность,
принадлежащяя тому же листу, если М
лежит на линии склеивания ∆k
с ∆k+1,
то ε
окрестность точки М составленная из
части ее ε
окрестности, принадлежащей ∆k
и распространяющ на нижнюю полуплоскость,
из части ε
окрестности, принадлежащей ∆k+1
и рапространяющ в верхнюю полуплоскость,
а также из εинтервалов,
лежащих на L0
и симметрично относительно Мпостроенная
n-листная
область называется Римановой
поверхностью
функции
листа ∆k
(k=0,1,2,…,n-2)с
верхним краем такого же разреза листа
∆k+1
Свободный верхний край разреза L0
листа ∆0
склеим с нижним краем разреза ∆n+1
Если
точка М
– внутренняя для листа ∆k
(∆k+1),
то у нее существует ε окрестность,
принадлежащяя тому же листу, если М
лежит на линии склеивания ∆k
с ∆k+1,
то ε
окрестность точки М составленная из
части ее ε
окрестности, принадлежащей ∆k
и распространяющ на нижнюю полуплоскость,
из части ε
окрестности, принадлежащей ∆k+1
и рапространяющ в верхнюю полуплоскость,
а также из εинтервалов,
лежащих на L0
и симметрично относительно Мпостроенная
n-листная
область называется Римановой
поверхностью
функции
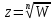
9. Экспоненциальная функция еz. Риманова поверхность функции Z = Ln(W)
Из равенства
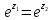 следует,
что
следует,
что
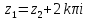 ,
так что областью однолистности
,
так что областью однолистности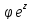 является
любая полоса шириной
является
любая полоса шириной действительной
оси. Разделим плоскость (z)
на совокупность полос
действительной
оси. Разделим плоскость (z)
на совокупность полос
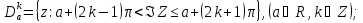 При отображенииW=ez
полосе
При отображенииW=ez
полосе соответствует вся плоскость ! с удаленной
из нее точкойW=0.
Открытая часть полосы
соответствует вся плоскость ! с удаленной
из нее точкойW=0.
Открытая часть полосы
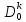 , т.е. области
, т.е. области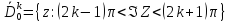 отображ
на
отображ
на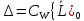 гдеL0
– отрицательная и действительная оси,
гдеL0
– отрицательная и действительная оси,
 А прямые
А прямые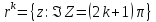 отображ наL0
Из
равенства
отображ наL0
Из
равенства
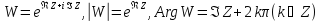 Отсюда
Отсюда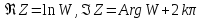 , следовательно все значения функцииLnW,
обратной к функции W=ezдля
, следовательно все значения функцииLnW,
обратной к функции W=ezдля
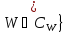 определяется
по формуле:
определяется
по формуле: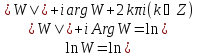
В областьи∆
имеем счетное множество однозначных
ветвей LnkW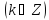 функцииLnW,
каждый из которых отображает ∆
на
функцииLnW,
каждый из которых отображает ∆
на
 В
точкеW=1
ветвь LnkWпринимает
значение
В
точкеW=1
ветвь LnkWпринимает
значение
 ;
оно может быть использовано для выделения
;
оно может быть использовано для выделения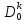 среди всех других рассматриваемых
полос. Пусть
среди всех других рассматриваемых
полос. Пусть и фиксировано, аz0
– значение LnW,
принадлежащее
и фиксировано, аz0
– значение LnW,
принадлежащее
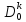 Переместим точкуWот
точки W0по
окрестности|W|=|W0|
против часовой стрелелки до той же точки
W0При
этом ArgWвозрастает
на
Переместим точкуWот
точки W0по
окрестности|W|=|W0|
против часовой стрелелки до той же точки
W0При
этом ArgWвозрастает
на
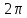 и
точкеW0будет
соответствовать точка
и
точкеW0будет
соответствовать точка
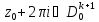 иначе
говоря, ветвьLnkWперейдет
в ветвь
иначе
говоря, ветвьLnkWперейдет
в ветвь
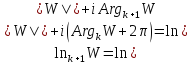 с
помощью многократного повторения можно
перейти от заданной ветвиLnkW
к другой его ветви.
с
помощью многократного повторения можно
перейти от заданной ветвиLnkW
к другой его ветви.
Рассмотри счетное
множество областей
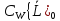 которое обозначим …,∆-2,∆-1,∆0,∆1,∆2,…
Будем считать их наложенными друг на
друга в порядке возрастания номеров.
Склеим
верхний край разреза
которое обозначим …,∆-2,∆-1,∆0,∆1,∆2,…
Будем считать их наложенными друг на
друга в порядке возрастания номеров.
Склеим
верхний край разреза
 листа ∆k+1Бесконечнолистная
поверхность получающаяся как результат
указанных объединений листов ∆k
называется Римановой
поверхностью
функции z=LnW
листа ∆k+1Бесконечнолистная
поверхность получающаяся как результат
указанных объединений листов ∆k
называется Римановой
поверхностью
функции z=LnW
ФункцияW=ez
голоморфно отображается
 на риманову поверхность функциюz=LnW
. Точка W=0
при обходе которой совершается переход
с одного лиса на другой называется
трансцендентной
точкой
ветвления функции z=LnW
на риманову поверхность функциюz=LnW
. Точка W=0
при обходе которой совершается переход
с одного лиса на другой называется
трансцендентной
точкой
ветвления функции z=LnW