
Пожаркова_ТАУ_ЛР_9434
.pdf
61
Построим в ПК «МВТУ» частотные характеристики САУ, модель которой представлена на рис.5.9, где параметры динамического звена
соответствуют W (p) |
k |
|
10 |
. |
|
|
|||
РЦ |
Tp 1 |
0.1p 1 |
||
|
||||
Рис.5.9
В модели при помощи блоков «В память» указаны входная (g) и выходная (y) величины, необходимые для частотного анализа.
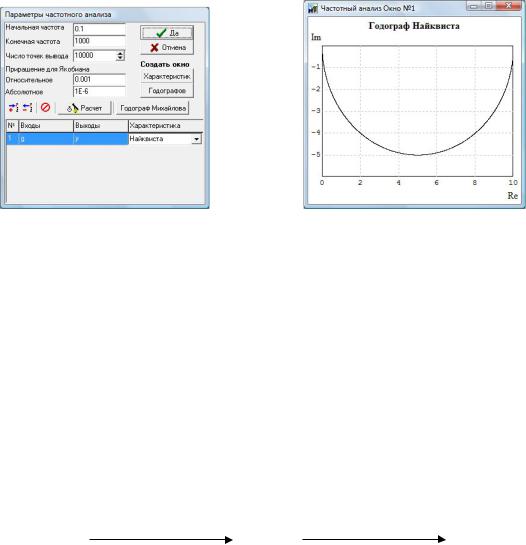
Для построения вещественной, мнимой, амплитудной, фазовой и логарифмической амплитудной частотных характеристик в диалоговом окне «Параметры частотного анализа» (рис.5.10), вызываемом из меню Анализ/Частотный анализ, необходимо выбрать Создать окно/Характеристик, затем задать частотный диапазон (поля Начальная частота, Конечная частота), входы, выходы и выбрать одну или несколько анализируемых характеристик (Вещественная, Мнимая, АЧХ, ЛЧХ, ВЧХ). В результате расчета получены частотные характеристики, приведенные на рис.5.11-5.13.
Рис.5.10 |
Рис.5.11 |
Рис.5.12 |
Рис.5.14 |
62
Для построения годографа АФЧХ в диалоговом окне «Параметры частотного анализа» необходимо выбрать Создать окно/Годографов и в поле «Характеристика» выбрать «Найквиста» (рис.5.14). В результате расчета получена АФЧХ, приведенная на рис.5.15.
Рис.5.14 Рис.5.15
Частотные характеристики, полученные в ПК «МВТУ» совпадают с построенными в Mathcad (рис.5.6-5.7).
5.5.ФИЗИЧЕСКИЙ СМЫСЛ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
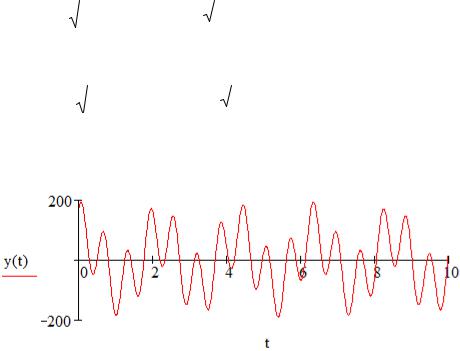
Пусть на вход системы (рис.5.16) подается сигнал x(t), равный сумме синусоидальных составляющих с разными амплитудами Xi, частотами i и
начальными фазами X i :
n
x(t) Xi sin( it Xi )
i 1
n |
|
n |
Xi sin( it Xi) |
|
Yi sin( it Yi) |
i 1 |
W(j ) |
i 1 |
|
|
|
Рис.5.16
В соответствии с принципом суперпозиции выходной сигнал системы
n
y(t) будет представлять собой сумму сигналов Yi sin( it Yi), каждый из
i 1
которых Yi sin( it Yi) есть реакция системы на соответствующую входную гармонику Xi sin( it X i) (рис.5.16).
При этом амплитуду и фазу каждой из составляющей выходного
сигнала можно вычислить по выражениям: |
|
Yi Xi A( i ), |
(5.3) |
63 |
|
где A( i ) - значение АЧХ на частоте i ; |
|
Yi Xi ( i), |
(5.4) |
где ( i) - значение ФЧХ на частоте i .
Поскольку любой сигнал можно разложить в ряд Фурье, представляющий сумму гармоник синуса и косинуса, то частотная передаточная функция W(j ), определяющая реакцию системы на гармонические колебания всех возможных частот, позволяет, пользуясь принципом суперпозиции, найти реакцию линейной системы на произвольное воздействие.
Выражения (5.3) и (5.4) также позволяют решать и обратную задачу – определение АЧХ и ФЧХ по известным амплитудам и фазам входного и выходного сигнала системы, измеряемых на ряде частот.
Построим установившуюся реакцию объекта управления с
передаточной функцией W (p) |
k |
(k 10, |
T 0.1) на гармоническое |
|||
|
|
|||||
|
РЦ |
Tp 1 |
|
|
|
|
|
|
|
|
|
||
воздействие |
x(t) X1 sin( 1t X1) X2 |
cos( 2t X 2), |
где |
|||
X1 9, 1 3, |
X1 1; X2 15, 2 |
10, |
X1 5. |
|
|
|
Обозначим выходной сигнал объекта управления y(t). В соответствии с принципом суперпозиции и выражениями (5.3) и (5.4) он равен
y(t) Y1 sin( 1t Y1) Y2 cos( 2t Y2),
где
Y1 X1 A( 1) X1 |
10 |
|
|
9 |
|
|
10 |
|
86, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 0.01 2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 0.01 32 |
||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Y1 |
X1 |
( 1) X1 arctg(0.1 1) 1 arctg(0.1 3) 1.3, |
||||||||||||||||||
Y2 X2 A( 2) X |
10 |
|
|
|
|
15 |
10 |
|
|
|
106, |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 0.01 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
1 0.01 102 |
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Y 2 |
X 2 |
( 2) X 2 arctg(0.1 2) 5 arctg(0.1 10) 5.8. |
||||||||||||||||||
|
Таким образом, |
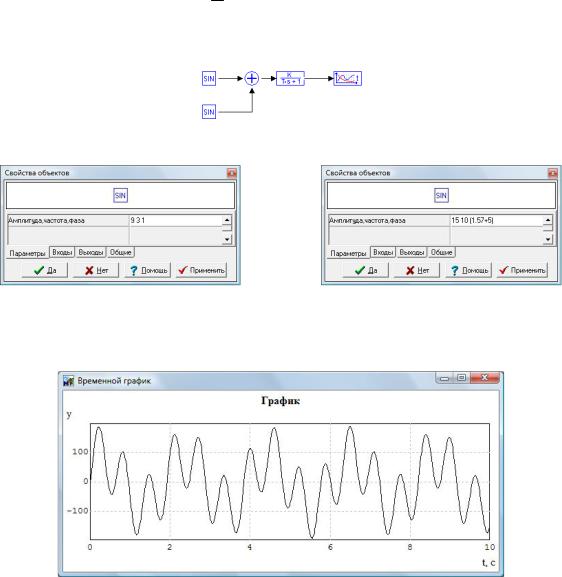
y(t) 86sin(3t 1.3) 106cos(10t 5.8). График |
||||||||||||||||||
выходного сигнала ОУ, построенный в Mathcad, приведен на рис.5.17.
Рис.5.17
|
64 |
|
|
|
Для |
задания |
входного |
|
воздействия |
x(t) X1 sin( 1t X1) X2 cos( 2t X 2) |
в |
МВТУ |
используется |
|
суммирование двух синусоидальных сигналов (рис.5.18-5.20), в параметрах одного из которых (рис.5.20) учитывается фазовый сдвиг между функциями
синус и косинус, равный 1.57, т.е. данный источник модулирует
2
косинусоиду.
Рис.5.18
Рис.5.19 |
Рис.5.20 |
График выходного сигнала ОУ (рис.5.21) аналогичен полученному в
Mathcad (рис.5.17).
Рис.5.21
ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РАБОТЫ
1.Получить аналитические выражения амплитудной (АЧХ), фазовой (ФЧХ), вещественной (ВЧХ), мнимой (МЧХ) и амплитудно-фазовой (АФЧХ) частотных характеристик разомкнутой системы (рис.1.17) по задающему воздействию. Построить их графики.
65
2.Построить асимптотическую логарифмическую амплитудную и логарифмическую фазовую частотные характеристики разомкнутой системы (рис.1.17) по задающему воздействию.
3.Построить установившуюся реакцию разомкнутой системы (рис.1.17) на гармоническое воздействие g t G1 sin( 1t) G2 cos( 2t 2).
4.Выполнить пункты 1-3 на ЭВМ, сравнить полученные результаты.
СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
исходные данные, все промежуточные аналитические выводы, схемы моделей, значения параметров и графики в форматах Mathcad и ПК «МВТУ», в которых должны быть отражены все исследования, проведенные в работе согласно заданию;
выводы по каждому пункту задания, где предполагается проведение исследований;
общие выводы по всей работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Как осуществляется преобразование Фурье?
2.Зачем нужны частотные характеристики? Какое их функциональное назначение?
3.Какие частотные характеристики вы знаете? Перечислите особенности их вычислений и построения.
4.Что такое ЛАЧХ и АЛАЧХ? Назовите особенности их построения.
Лабораторная работа №6. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САУ
Цель – изучить методы оценки устойчивости линейных непрерывных систем автоматического управления.
ОБЩИЕ СВЕДЕНИЯ 6.1.ПОНЯТИЕ УСТОЙЧИВОСТИ
Важным показателем систем автоматического управления является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы

66
ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки, то система называется неустойчивой.
6.2.НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ УСТОЙЧИВОСТИ
Необходимое и достаточное условие устойчивости формулируется следующим образом: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательную вещественную часть (лежали в левой полуплоскости комплексной плоскости).
Если хотя бы один корень располагается в правой полуплоскости, то система неустойчива.
Ось ординат комплексной плоскости называют границей устойчивости. Возможны два случая нахождения системы на границе устойчивости:
1. Апериодическая граница устойчивости. Условием нахождения на ней является наличие одного корня в начале координат p1 0 и остальных корней в левой полуплоскости.
2. Колебательная граница устойчивости – если система имеет пару чисто мнимых корней, а все остальные корни лежат в левой полуплоскости.
Необходимым условием устойчивости линейных систем любого порядка является положительность знаков всех коэффициентов характеристического уравнения.
|
Пример. Оценим |
устойчивость |
системы (рис.6.1), |
где |
W (p) |
1 |
, |
|||
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
p |
|
|
|
|
|
|
|
|
|
|
|
|
W2 |
(p) |
A0 p A1 |
|
4p 2 |
|
, в разомкнутом |
и |
замкнутом |
||
(A0 p 1)(B0 p 1) |
|
|
||||||||
|
|
|
(4p 1)(5p 1) |
|
|
|
|
|||
состоянии. |
|
|
|
|
|
|
|
|
||
g t |
t |
y t |
|
W2(p) |
W1(p) |
Рис.6.1
Передаточная функция разомкнутой цепи:
WРЦ(p) W1(p) W2(p) |
4p 2 |
|
|
. |
|
|
||
|
p(4p 1)(5p 1) |
|
Характеристическое уравнение разомкнутой системы: p(4p 1)(5p 1) 0.
67
Корни характеристического уравнения:
p1 0
p2 0.25 p3 0.2
Поскольку один корень характеристического уравнения p1 0 и остальные корни лежат в левой полуплоскости, система в разомкнутом состоянии находится на апериодической границе устойчивости.
Характеристическое уравнение замкнутой системы: p(4p 1)(5p 1) 4p 2 0
20p3 9p2 5p 2 0
Корни характеристического уравнения замкнутой системы: p1 0.421
p2,3 0.015 0.487j
Поскольку все корни характеристического уравнения лежат в левой полуплоскости, система в замкнутом состоянии устойчива.
6.3.КРИТЕРИИ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ
Вычисление корней характеристического уравнения высокого порядка зачастую затруднительно. Поэтому для исследования устойчивости систем разработаны критерии (правила), позволяющие судить о расположении корней на комплексной плоскости без их расчета.
Критерии устойчивости – это математические методы, позволяющие судить о принадлежности корней характеристического уравнения левой полуплоскости без решения этого уравнения.
Существуют два основных класса критериев устойчивости:
1.Алгебраические – основанные на проверке ряда соотношений, составленных из коэффициентов характеристического уравнения.
2.Частотные – основанные на построении частотных характеристик системы и исследовании их внешнего вида.
6.4.АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ ГУРВИЦА
Линейная система, характеристический полином (знаменатель
передаточной функции) которой равен |
D(p) a |
pn a pn 1 |
a |
pn 2 ... a |
, |
|
0 |
1 |
2 |
n |
|
где a0 0, устойчива, если положительны n главных определителей матрицы Гурвица:
68
a1 |
a3 |
a5 ... |
0 |
|
|
a2 |
a4 ... |
0 |
|
a0 |
|
|||
0 |
a1 |
a3 ... |
0 |
|
|
... |
... ... |
... |
|
... |
|
|||
|
0 |
0 ... |
|
|
0 |
an |
|||
Для оценки устойчивости системы необходимо вычислить определители Гурвица i (i 1, 2, ..., n), которые получают из матрицы
Гурвица путем отчеркивания равного числа строк и столбцов в левом верхнем углу матрицы.
Так как в последнем столбце матрицы все элементы, кроме нижнего, равны нулю, то последний n-й определитель матрицы Гурвица: n an n 1. Следовательно система устойчива, если положительны (n 1) главных определителей матрицы Гурвица и an 0:
i |
0 |
при i 1, 2, ..., |
n 1 |
|
0 |
|
|
an |
|
|
Если первые (n 2) определителя Гурвица больше 0, а (n 1) определитель Гурвица равен нулю n 1 0, то система находится на колебательной границе устойчивости.
Если в исходной системе коэффициент an 0, а все остальные коэффициенты имеют один знак, то такая система имеет один нулевой корень и может находиться на апериодической границе устойчивости. Вынеся за скобки нулевой корень и понизив порядок уравнения, новую систему исследуют на устойчивость по критерию Гурвица, делая соответствующий вывод.
Пример. Оценим устойчивость системы (рис.6.1) в разомкнутом и замкнутом состоянии.
Характеристическое уравнение разомкнутой системы: p(4p 1)(5p 1) 0
20p3 9p2 p 0
В характеристическом уравнении an 0, следовательно, система, возможно, находится на апериодической границе устойчивости. Понизим порядок и исследуем устойчивость новой системы:

69
p(20p2 9p 1) 0
20p2 9p 1 0, |
n 2 |
a0
a0
a1
a0
20, a1 9, a2 1
0, an a2 0
Составим матрицу Гурвица:
0 |
|
9 |
0 |
|
|
|
|
a2 |
20 |
1 |
|
Найдем определители матрицы Гурвица:
1 n 1 9 0
Поскольку коэффициент an 0 и n 1 0, система в разомкнутом состоянии находится апериодической границе устойчивости.
Характеристическое уравнение замкнутой системы: p(4p 1)(5p 1) 4p 2 0
20p3 9p2 5p 2 0 |
n 3 |
||||||
a0 |
20, |
a1 9, |
a2 |
5, |
a3 2 |
||
a0 |
0, an a3 0 |
|
|
||||
|
|
Составим матрицу Гурвица: |
|||||
a1 |
a3 |
0 |
9 2 |
0 |
|||
a a |
0 |
|
20 5 |
0 |
|||
|
0 |
2 |
a |
|
|
9 |
|
0 |
a |
|
0 |
2 |
|||
|
|
1 |
3 |
|
|
|
|
Найдем определители матрицы Гурвица:
1 9 0
92
2 20 5 9 5 20 2 5 0
Так как (n-1)=2 определителей матрицы Гурвица положительны, то система в замкнутом состоянии устойчива.
6.5.ЧАСТОТНЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА
Порядок применения критерия Михайлова следующий:
1.Записывается характеристический полином разомкнутой или замкнутой системы: D(p) a0 pn a1pn 1 a2 pn 2 ... an.
2.В характеристический полином подставляется p j и записывается уравнение D(j ) U( ) jV( ).
70
3. Строится кривая D(j ) на комплексной плоскости.
Характеристику D(j ), построенную на комплексной плоскости, называют годографом Михайлова. Аналогично годографу АФЧХ, годограф Михайлова представляет собой геометрическое место концов векторов (годографов), соответствующих частотной функции D(j ) при изменении частоты от нуля до бесконечности.
Если система n-го порядка устойчива, то годограф Михайлова при изменении частоты от нуля до бесконечности начинается на вещественной положительной полуоси, имеет вид раскручивающейся спирали и последовательно проходит n квадрантов комплексной плоскости против часовой стрелки. Другими словами, для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции
D(j ) при изменении частоты от нуля до бесконечности равнялось бы n . 2
Условием нахождения системы на колебательной границе устойчивости является прохождение годографа Михайлова через начало координат.
Пример. Оценим устойчивость системы (рис.6.1) в замкнутом состоянии.
Характеристический полином замкнутой системы 3-го порядка (n=3):
D(p) p(4p 1)(5p 1) 4p 2 20p3 9p2 5p 2.
Заменим p j :
D( j ) 20( j )3 9( j )2 5j 2 20 3 j 9 2 5 j 29 2 2 5 20 3 j,
U( ) 9 2 2,
V( ) 5 20 3.
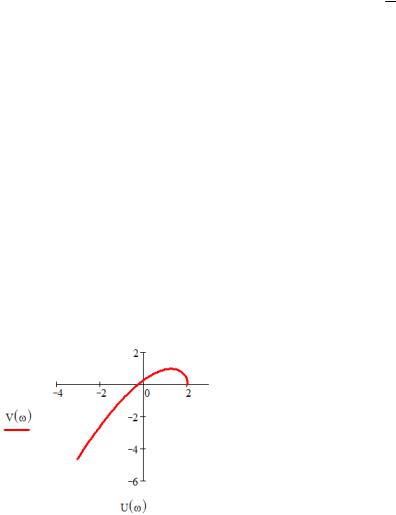
Построим годограф Михайлова:
Рис.6.2
Годограф Михайлова начинается на вещественной положительной полуоси, имеет вид раскручивающейся спирали и последовательно проходит
