
Пожаркова_ТАУ_ЛР_9434
.pdf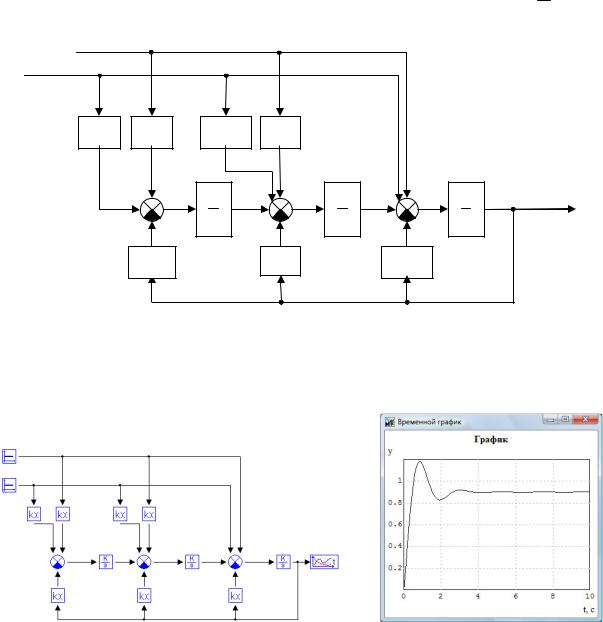
41
По последнему уравнению составим пооператорную структурную
схему (рис.3.3). В схеме будет три идеальных интегрирующих звена 1 . p
F(p)
U(p)
70 |
20 |
14.5 |
|
12 |
|
|
|
|
1 |
|
1 |
1 |
Y(p) |
|
x1 |
p |
x1 |
x2 p x2 |
x3 p x3 |
|
|
100 |
|
|
35 |
12.5 |
|
Рис.3.3
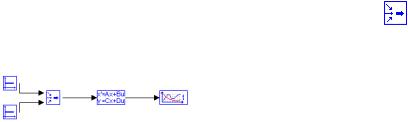
Создадим пооператорную структурную схему в ПК «МВТУ» (рис.3.4). Выходной сигнал схемы (рис.3.5) совпадает в полученным ранее (рис.2.14) по модели ОУ в виде передаточных функций.
Рис.3.4 |
Рис.3.5 |
Введем вспомогательный вектор Х с компонентами X AX BU . За
Y CX DU
компоненты вектора примем выходные сигналы каждого из интеграторов (переменные состояния) на пооператорной схеме (рис.3.3). Составим систему уравнений для переменных состояния и уравнение для выходного сигнала:
42
x1(t) 100x3(t) 70u(t) 20f (t)
x2(t) x1(t) 35x3(t) 14.5u(t) 12f (t)x3(t) x2(t) 12.5x3(t) u(t) f (t)
y(t) x3(t)
Запишем полученные уравнения в канонической векторно-матричной форме:
|
|
|
|
|
|
|
|
|
|
|
|
X |
AX BU , |
||
где |
|
|
|
|
|
|
|
|
|
|
|
Y CX DU |
|||
x1 |
|
|
x1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
u |
|||||
|
|
|
|
|
|
|
|
, Y y , |
|
|
|||||
X |
|
|
, |
X |
|
x2 |
|
V , |
|||||||
|
x2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
f |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
||
|
0 |
0 |
100 |
|
|
|
70 |
20 |
|
||||||
A |
|
|
0 |
35 |
|
|
|
B |
|
|
12 |
|
, |
||
1 |
, |
|
|
14.5 |
|
||||||||||
|
0 |
1 |
12.5 |
|
|
|
|
1 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C 0 0 |
1 , |
|
D 0 |
0 . |
|
|
|
|
|||||||
ПК «МВТУ» предоставляет возможность задать ОУ в векторно-
матричной форме при помощи блока 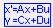 «Переменные состояния» (библиотека «Динамические») (рис.3.6). Параметры блока «Переменные состояния» (рис.3.7) заданы в соответствии с матрицами A, B, C, D, описывающими данный ОУ. Следует учитывать, что элементы матриц записываются по столбцам. Для объединения входных (управляющего и
«Переменные состояния» (библиотека «Динамические») (рис.3.6). Параметры блока «Переменные состояния» (рис.3.7) заданы в соответствии с матрицами A, B, C, D, описывающими данный ОУ. Следует учитывать, что элементы матриц записываются по столбцам. Для объединения входных (управляющего и
возмущающего воздействий) в один вектор V используется блок «Мультиплексор» (библиотека «Векторные»).
Рис.3.6 Модель ОУ в ВМФ
43
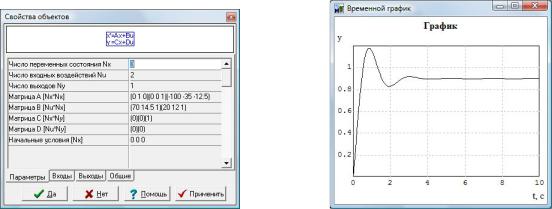
Рис.3.7 Окно настройки параметров |
Рис.3.8 Временной график выходного |
блока «Переменные состояния» |
сигнала ОУ в ВМФ |
Временная характеристика выходного сигнала ОУ (рис.3.8), задаваемого в векторно-матричной форме с помощью блока «Переменные состояния», совпадает с полученными ранее для ОУ, представленного в виде передаточной функции (рис.2.14) и пооператорной структурной схемы (рис.3.5).
ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РАБОТЫ
1.Используя результаты выполнения п.1. лабораторной работы №1, составить пооператорную структурную схему объекта управления (рис.1.17). Подтвердить результаты моделированием в ПК «МВТУ».
2.Записать модель объекта управления в векторно-матричной форме. Подтвердить результаты моделированием в ПК «МВТУ».
СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
исходные данные, все промежуточные аналитические выводы, схемы моделей, значения параметров и графики в формате ПК «МВТУ», в которых должны быть отражены все исследования, проведенные в работе согласно заданию;
выводы по каждому пункту задания, где предполагается проведение исследований;
общие выводы по всей работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Алгоритм составления уравнений состояний.
2.Построение пооператорной структурной схемы
44
Лабораторная работа №4. ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ САУ
Цель – изучить методы получения аналитических выражений временных характеристик линейных непрерывных САУ.
ОБЩИЕ СВЕДЕНИЯ
Характеристика системы - это ее реакция на определенное входное воздействие. Для линейных звеньев и линейных систем в целом характеристика полностью определяет их динамические свойства, так как к линейным звеньям и системам применим принцип суперпозиции, позволяющий по реакции линейного элемента на какое-либо известное воздействие найти его реакцию на воздействие произвольного вида.
В качестве входных воздействий, на которые ищется реакция звена, приняты воздействия, описываемые элементарными математическими функциями, то есть такими, на которые можно разложить любые произвольные функции. В теории управления в качестве элементарных функций используются:
единичная ступенчатая функция 1(t);
единичная импульсная или дельта-функция (t);
гармоническая функция X0 sin( 0t).
Существуют временные (переходная и импульсная функции) и частотные характеристики.
4.1.ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ УПРАВЛЕНИЯ
Переходная характеристика системы.
1 t |
|
h t |
W(p) |
||
|
|
|
Рис.4.1
Переходная характеристика h(t) представляет собой реакцию системы (рис.4.1) на единичную ступенчатую функцию (функцию Хэвисайда) (рис.4.2):
|
|
|
1(t) |
|
|
|
при |
t 0, |
1 |
|
|
|
|||||
0 |
|
|
|||
1(t) |
при |
t 0. |
|
|
|
1 |
|
|
|||
0 |
t |
||||
|
|
|
Рис.4.2
45
Изображение по Лапласу единичной ступенчатой функции L 1(t) 1 , p
тогда переходная характеристика системы: |
|
|
|
h(t) L1 h(p) L1 |
|
1 |
W(p) . |
|
|||
|
|
|
|
|
p |
|
|
Импульсная характеристика системы.
t |
|
k t |
W(p) |
||
|
|
|
|
Рис.4.3 |
|
Импульсная характеристика (или весовая функция) k t представляет собой реакцию системы (рис.4.3) на -функцию (функцию Дирака) (рис.4.4):
|
|
|
|
(t) |
|
|
|
при |
t 0, |
|
|
|
|
0 |
|
|
|
|||
(t) |
при |
t 0. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||
|
|
|
|
0 |
|
t |
|
|
|
|
|
||
|
|
|
|
Рис.4.4 |
|
|
Изображение по Лапласу -функции |
L (t) 1, тогда |
импульсная |
||||
характеристика системы: |
|
|
|
|||
k(t) L 1 k(p) L 1 W(p) .
Импульсная и переходная характеристики связаны соотношением:
k(t) d h(t). dt
4.2.НАХОЖДЕНИЕ ОБРАТНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА. ТЕОРЕМА РАЗЛОЖЕНИЯ
Для перехода от реальных функций времени (оригиналов) к их изображениям по Лапласу и наоборот введены прямое и обратное интегральные преобразование Лапласа.
В общем случае для перехода от изображения F(p) к оригиналу f(t) необходимо выполнить обратное преобразование Лапласа:
1 |
F(p) |
1 c j |
pt |
|
|
|
f (t) L |
|
F(p) e |
|
dp, где p c |
j . |
|
|
|
|||||
|
|
j2 c j |
|
|
|
|
На практике для нахождения обратного преобразования Лапласа используют Теорему разложения.

46
Пусть изображение F(p) можно представить в виде дроби как
отношение полиномов F(p) B(p).
A(p)
Значения p, при которых выполняется условие F(p) 0, т.е. B(p) 0, называют нулями функции F(p). Значения p, при которых выполняется условие A(p) 0 (т.е. корни знаменателя), называют полюсами функции F(p). Тогда оригинал функции можно найти:
|
|
n |
|
|
|
f (t) L 1 F(p) Res F(p)ept , |
(4.1) |
||
|
|
i 1 pi |
|
|
где pi - полюса функции F(p). |
|
|
||
Если знаменатель функции F(p) можно представить в виде: |
|
|||
A(p) (p p )k1 |
(p p )k2 |
... (p p )kn , то |
p называют полюсом кратности |
|
1 |
2 |
n |
i |
|
ki . Если ki 1, то pi называют простым полюсом. Для простых полюсов ( ki 1) вычеты вычисляются по формуле:
Res F p ept lim p pi F p ept . |
(4.2) |
|
pi |
p pi |
|
Для полюсов кратности ki 1 вычеты вычисляются по формуле:
Res F p e |
pt |
|
1 |
|
|
|
dki 1 |
p p |
ki |
|
pt |
|
|
|
|
|
|
lim |
|
|
|
|
F p e |
|
|
(4.3) |
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ki 1 |
|
. |
|||||||
pi |
|
|
ki 1! |
|
|
i |
|
|
|
|
|
|||
|
|
p pi dp |
|
|
|
|
|
|
|
|||||
*
Если есть два комплексно сопряженных полюса pi 1 pi , то для суммы вычетов по ним справедливо:
|
pt |
|
|
pt |
|
pt |
|
|
||
Res F p e |
Res F p e |
2Re Res F p e |
|
|
||||||
|
|
|
|
|||||||
pi |
|
pi 1 |
|
|
|
pi |
|
|
(4.4) |
|
|
|
|
pt |
|
|
|
|
|||
|
|
|
|
|
|
|||||
2Re lim p pi F p e |
. |
|
|
|
||||||
|
|
|
|
|
||||||
p pi |
|
|
|
|
|
|
|
|
|
|
При этом, при расчете вычета Res F p ept в результате вычисления
pi
предела будет получена экспонента в комплексной степени. Для того, чтобы найти ее действительную часть, необходимо воспользоваться формулой Эйлера:
e j e (cos j sin ). |
(4.5) |
Пример 1. Найдем переходную и импульсную характеристики замкнутой системы по задающему воздействию, передаточная функция
10
которой yg (p) p2 3p 2.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
||
h(t) L1 h(p) L1 |
|
1 |
|
|
(p) L1 |
|
1 |
|
|
10 |
|
L1 |
|
10 |
|
. |
|||||||||||||
|
yg |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3p 2 |
|
3p |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
p p2 |
|
p2 |
2 p |
||||||||||
|
|
|
Выполним обратное преобразование Лапласа, используя (4.1). |
||||||||||||||||||||||||||
|
|
|
Найдем полюса (корни знаменателя) и определим их кратность: |
||||||||||||||||||||||||||
p2 3p 2 p 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
p2 3p 2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
32 4 2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p |
|
|
|
1 |
1 |
k 1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p2 |
|
3 |
1 |
|
2 k2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p3 0 k3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как все полюса простые, для нахождения всех вычетов применим формулу (4.2). Представим преобразуемое выражение в следующем виде:
|
|
|
|
1 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
1 |
|
|
10 |
|
|
|
|
|
3 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
pt |
|
||||||||||||||||
h(t) |
L |
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Res |
|
|
|
|
|
|
|
|
e |
. |
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
(p 1)(p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
3p 2 p |
|
|
|
|
|
|
2)p |
|
|
i 1 pi |
(p 1)(p 2)p |
|
|
|
||||||||||||||||||||||||||||||||||
Res |
|
|
|
|
|
10 |
|
ept |
lim |
p p |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
ept |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
p1 |
(p 1)(p 2)p |
|
|
p p1 |
|
|
1 |
|
|
(p 1)(p |
2)p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
pt |
|
|
|
|
10 |
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
10 |
|
t |
|
|
|
|
|
|
t |
|
|||||||||
lim |
p 1 |
|
|
|
|
|
|
|
e |
|
|
|
lim |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
e |
|
10e |
|
|
, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1 2)( 1) |
|
|
|
|||||||||||||||||||||||||||||||||||||
p 1 |
|
|
|
|
|
(p 1)(p 2)p |
|
|
|
p 1 (p 2)p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
10 |
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Res |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
lim |
p p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(p 1)(p 2)p |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
p2 |
|
(p 1)(p 2)p |
|
|
p p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
pt |
|
|
|
|
10 |
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
10 |
|
2t |
|
|
|
|
|
2t |
|
|
|||||||||
lim |
p 2 |
|
|
|
|
|
|
|
|
e |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
e |
|
5e |
|
|
, |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(p 1)(p 2)p |
|
|
|
(p 1)p |
|
|
|
|
|
( 2 1)( 2) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
p 2 |
|
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
10 |
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Res |
|
|
|
|
|
|
|
|
|
|
|
e |
|
lim |
p p3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
p3 |
|
(p 1)(p 2)p |
|
|
p p3 |
|
|
|
|
|
|
|
(p 1)(p 2)p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
pt |
|
|
|
10 |
|
|
|
|
0 |
|
|
|
|
|
||||||||
lim |
|
p 0 |
|
|
|
|
|
|
e |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
e |
|
|
5. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
p 0 |
|
|
|
|
|
(p 1)(p 2)p |
|
|
p 0 |
(p 1)(p 2) |
|
|
|
|
|
|
(0 1)(0 2) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
Таким образом, переходная характеристика |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
10 |
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
t |
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
h(t) Res |
|
|
|
|
|
|
|
e |
|
10e |
|
5e |
|
|
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
i 1 |
|
pi |
|
|
(p 1)(p 2)p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Найдем |
импульсную |
|
характеристику: |
|
|
k(t) |
h(t) 10 e t 10 e 2t . |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|||
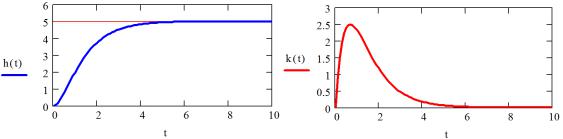
Графики переходной и импульсной характеристик приведены на рис.4.5.
48
Рис.4.5
Пример 2. Найдем переходную характеристику разомкнутой системы по задающему воздействию, передаточная функция которой
Wyg (p) |
|
|
|
|
5 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p(p 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
5 |
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
h(t) L |
|
|
h(p) L |
|
|
|
|
Wyg (p) |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|
|
p(p 1) |
|
|
|
|
p2(p |
1) |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Res |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
(p 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
i 1 pi |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
Выполним обратное преобразование Лапласа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Найдем полюса (корни знаменателя) и определим их кратность: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
p2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
p 0 |
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 1 |
|
|
|
k2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(4.3): |
Кратность первого полюса k1 2 1, поэтому воспользуемся формулой |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
pt |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
dk1 1 |
|
|
ki |
|
|
5 |
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Res |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
p p |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
p1 |
|
(p 1) |
|
|
|
|
|
k1 1! |
|
|
|
|
|
|
|
k1 1 |
|
i |
|
|
p |
(p 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
p p1 dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
d2 1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
pt |
|
|
|
|
d |
|
|
|
|
|
|
2 |
|
|
|
5 |
|
|
pt |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
p |
p |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
lim |
|
|
|
p 0 |
|
|
|
|
|
|
|
|
e |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
p |
(p 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
(p 1) |
|
|
|
|||||||||||||||||||||||||
|
|
2 1!p p1 dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 0 dp |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
d |
|
5 |
|
|
|
|
pt |
|
|
|
|
|
|
d ept |
|
|
|
|
|
|
|
ept |
t(p 1) ept |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
e |
|
lim 5 |
dp |
|
|
|
|
|
|
lim 5 |
|
|
|
(p 1) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
p 0 dp p 1 |
|
|
|
|
|
|
p 0 |
p 1 |
|
|
p 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
e0 t(0 1) e0 |
|
5(t 1) 5t 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
(0 1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Кратность второго полюса k2 1, поэтому воспользуемся формулой
(4.2):
49
|
|
|
|
5 |
|
|
|
pt |
|
|
|
|
|
|
|
5 |
|
|
|
pt |
|
|
|
5 |
|
pt |
|
||||
Res |
|
|
|
|
|
|
|
|
e |
|
|
lim |
p p2 |
|
|
|
|
|
e |
|
lim p 1 |
|
|
|
e |
|
|
||||
|
|
2 |
(p 1) |
|
p |
2 |
(p 1) |
p |
2 |
(p 1) |
|||||||||||||||||||||
p2 p |
|
|
|
|
|
p p2 |
|
|
|
|
p 1 |
|
|
|
|
||||||||||||||||
lim |
|
5 |
e |
pt |
5e |
t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
p 1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Таким образом, переходная характеристика |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
5 |
|
|
|
pt |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
h(t) Res |
|
|
|
|
|
|
|
e |
|
5t 5 5e |
|
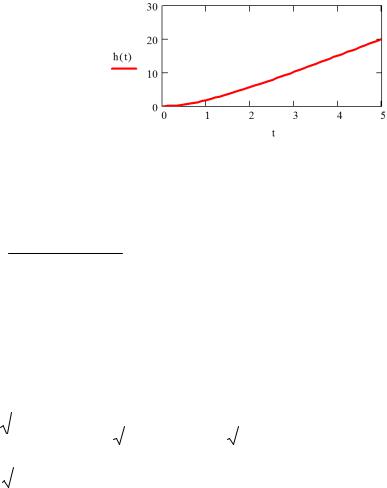
. Построим ее график (рис.4.6): |
|
||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
i 1 pi |
p |
|
(p 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рис.4.6
Пример 3. Найдем импульсную характеристику замкнутой системы по задающему воздействию, передаточная функция которой
p1
yg (p) 2p2 20p 68.
k(t) L1 k(p) L1 |
|
(p) L1 |
|
|
p 1 |
|
L1 |
|
|
p 1 |
. |
yg |
|
|
|
|
|
|
|
||||
|
|
2p2 |
|
|
2(p2 |
10p 34) |
|
||||
|
|
|
|
20p 68 |
|
|
|
||||
Выполним обратное преобразование Лапласа, используя (4.1.). Найдем полюса (корни знаменателя) и определим их кратность:
p2 10p 34 0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
52 34 |
|
|
|
|
|
|
|
|||||
p |
|
5 25 34 5 9 5 3j |
k 1 |
||||||||||||
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p2 |
|
5 |
|
52 34 |
5 3j |
k2 1 |
|
||||||||
|
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Корни p1 и p2 - комплексно сопряженные. Воспользуемся формулами
(4.4) и (4.5):
50
2 |
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
pt |
|
|
|
|||||||||||
k(t) Res |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
Res |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
||||||||||||||
2(p |
2 |
10p 34) |
|
|
|
2 |
10p 34) |
|
|
|||||||||||||||||||||||||||||||||||||
i 1 |
pi |
|
|
|
|
p1 |
|
2(p |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
p 1 |
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
pt |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Res |
|
2 |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|||||||
|
10p 34) |
|
2Re Res |
2(p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
p2 2(p |
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
10p 34) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
p p |
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2Re lim |
|
|
|
|
|
|
ept |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
2(p |
10p 34) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
p |
p1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
p (5 3j) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
||||||||||||||||||||||
2Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
p 5 3 j |
|
|
|
|
|
|
|
|
|
|
2 p (5 3j) p (5 3j) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
pt |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|||||||||||||||||||
2Re |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Re |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 p (5 3j) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
p 5 3 j |
|
|
|
|
|
|
p 5 3 j 2 p 5 3j |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
5 3j 1 |
|
|
e |
(5 3 j)t |
|
|
6 3j |
e |
(5 3 j)t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 6 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 5 3j 5 3j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
6 3j
2Re 12 j
1
2Re j
2
1
sin(3t)
2
Таким
k(t) sin(3t)
e |
(5 3 j)t |
|
6 j 3 |
e |
5t 3t j |
|
||
|
|
2Re |
|
|
|
|
||
|
|
|
||||||
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
||||
1 |
|
5t |
|
|
1 |
|
1 |
|
5t |
|
|
|
|
e |
|
cos(3t) j sin(3t) |
2 |
|
sin(3t) |
|
cos(3t) e |
|
|
|
|
|
4 |
|
|||||||
4 |
|
|
|
2 |
|
|
|
||||
cos(3t) e5t.
образом, импульсная характеристика
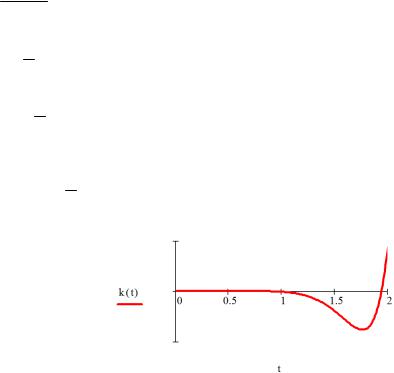
1cos(3t) e5t. Построим ее график (рис.4.7):
2
Рис.4.7
Пример 4. Найдем переходную и импульсную характеристики по задающему воздействию для замкнутой системы (рис.1.17), объект управления которой рассмотрен в разделе 1.5, Kp=10. Осуществим расчет в
Mathcad (рис.4.8-4.9).
