Пожаркова_ТАУ_ЛР_9434

На рис.2.19 приведены примеры использования перечисленных команд. Следует отметить, что большинство команд меню Simbolic обрабатывают как выражения, заданные в явном виде, так и заданные при помощи функций.

Рис.2.19

2. Решение уравнений, систем уравнений, неравенств.

Для решения уравнений, систем уравнений, неравенств в Mathcad (рис.2.20) используется команда solve меню Simbolic (рис.2.18).

Рис.2.20

32

3. Нахождение обратного преобразования Лапласа.

Для выполнения обратного преобразования Лапласа для заданного выражения (рис.2.21) используется команда invlaplace меню Simbolic.

Рис.2.21

4.Замена переменной.

Для подстановки в выражение вместо указанной переменной

некоторого другого выражения или константы (рис.2.22) используется команда substitute меню Simbolic.

Рис.2.22

5. Комплексные функции.

Мнимая единица в Mathcad задается комбинацией клавиш «1i». Вычисление значений выражений с комплексными константами осуществляется непосредственным нажатием на клавишу «=». Для работы c комплексными функциями (вычисление действительной и мнимой частей, амплитуды, фазы) (рис.2.23) используется команда complex меню Simbolic.

33

Рис.2.23

6. Построение графиков.

Для вставки графика используется меню Graph

Рис.2.25

Функции по обеим осям могут быть заданы параметрически (рис.2.26).

34

Рис.2.26

Параметры графика (линии сетки, тип осей, тип и толщина линий и т.д.) редактируются в меню Format (рис.2.28), вызываемом из контекстного меню (рис.2.27) или двойным нажатием на левую кнопку мыши.

При работе с графиком можно воспользоваться функцией увеличения (Zoom) (рис.2.29) или отображения координат точки графика (Trace) (например, для нахождения координат точки пересечения двух графиков) (рис.2.30).

35

ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕДЕНИЯ РАБОТЫ

1.В ПК «МВТУ» создать модель ОУ по его структурной схеме (рис.1.18) и вычисленным в п.1 лабораторной работы №1 передаточным функциям динамических звеньев.

2.По модели в ПК «МВТУ» определить передаточные функции ОУ по управляющему u(t) и возмущающему f(t) воздействиям. Результаты

сравнить с полученными в п.1 лабораторной работы №1.

3.В ПК «МВТУ» по функциональной схеме САУ (рис.1.17) и результатам п.1 составить структурную схему САУ. По модели в ПК «МВТУ» определить передаточные функции замкнутой системы с единичной отрицательной обратной связью по задающему g(t) и возмущающему

f(t) воздействиям относительно выходной координаты y(t) и ошибки(t). Результаты сравнить с полученными в п.3 лабораторной работы №1.

4.

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

исходные данные, все промежуточные аналитические выводы, схемы моделей, значения параметров и графики в формате ПК «МВТУ», в которых должны быть отражены все исследования, проведенные в работе согласно заданию;

выводы по каждому пункту задания, где предполагается проведение исследований;

общие выводы по всей работе.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что такое передаточная функция?

2.Перечислите способы соединений динамических звеньев.

3.Какие правила преобразования структурных схем вы знаете?

Лабораторная работа №3. ПООПЕРАТОРНАЯ СТРУКТУРНАЯ СХЕМА. ВЕКТОРНО-МАТРИЧНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ ОБЪЕКТА УПРАВЛЕНИЯ

Цель – представить объект управления в виде пооператорной структурной схемы, научиться составлять векторно-матричную форму.

ОБЩИЕ СВЕДЕНИЯ

36

3.1.МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИНАМИЧЕСКИХ СИСТЕМ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ (ВМФ)

Развитие высококачественных систем управления потребовало разработки новых методов их анализа и синтеза. Современная теория управления, основу которой заложили известные работы Л.С.Понтрягина, Р.Беллмана и Р.Калмана, базируется на описании систем в пространстве состояний.

Описание в пространстве состояний представляет собой общий взгляд на любые системы и пригодно для исследования и проектирования сложных систем с многими входами и выходами, то есть многомерных и многосвязных систем. С математической точки зрения анализ систем в пространстве состояний означает использование методов матричного исчисления и векторного анализа.

Понятие состояния является определяющим в современной теории управления. Под состоянием системы понимается минимально-необходимый набор переменных величин системы x1, x2, ... xn, способных однозначно и

единственным образом определить положение системы в любой момент времени t. Совокупность переменных величин x1, x2, ... xn образует n-мерное

пространство состояний. Вектор X с компонентами x1, x2, ... xn называется вектором состояния:

x1

x X 2 .

...

u1 y1 u2 y2

um yr

Рис.3.1

Поведение системы во времени можно характеризовать не только выходными величинами, но и промежуточными переменными координатами в цепи системы - переменными состояния xi , число которых равно порядку

37

системы n. Таким образом, получается n-мерный вектор состояния X, множество возможных положений которого образует векторное пространство, называемое пространством состояний системы.

В общем случае линейная система, описывается системой дифференциальных уравнений в нормальной форме и может быть определена следующей векторно-матричной формой:

Y CX DU

где X - вектор состояния системы,

Y - вектор выходных управляемых величин,

U - вектор внешних воздействий (задающих и возмущающих), А, В, С, D - матрицы системы.

Рассмотрим одну из методик составления векторно-матричных дифференциальных уравнений для системы с двумя входами и одним выходом (рис.1.4). Согласно структурной схеме:

Y(p) U(p)Wyu(p) F(p)Wyf (p), где

Рассмотрим частный случай m k n 1. Тогда слагаемые в правой части уравнения можно сгруппировать следующим образом:

38

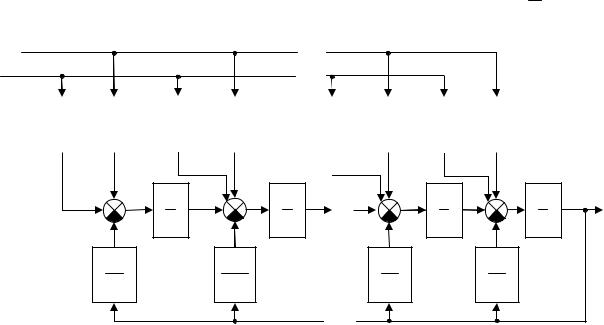
Полученному уравнению соответствует пооператорная структурная

схема (рис.3.2), содержащая n идеальных интегрирующих звеньев 1 . p

F(p)

U(p)

Рис.3.2

На схеме отмечены переменные состояния x1, x2, ..., xn .

Переменные состояния в общем случае определяются выражениями: