Пожаркова_ТАУ_ЛР_9434

12

Функции Wyu(p) и Wyf (p) называют передаточными функциями ОУ,

соответственно, по управляющему u t и возмущающему f t воздействиям. В общем случае передаточной функцией системы (звена) W(p)

называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях и равных нулю воздействиях на остальных входах элемента.

Действительно, если f (t) 0, то F(p) 0, тогда из уравнения (1.5)

следует Wyu(p) Y(p) .

U(p)

Аналогично, если u(t) 0, то U(p) 0, тогда Wyf (p) Y(p) .

F(p)

Передаточная функция имеет важное основополагающее значение в классической теории управления. Она устанавливает связь в динамическом режиме между выходной и входной величинами элемента и полностью характеризует его динамические свойства. Передаточная функция не зависит от вида конкретного входного сигнала и определяется структурой и параметрами объекта. При прохождении сигнала через звено, изображение сигнала умножается на передаточную функцию, преобразуясь в изображение выходного сигнала.

Понятие передаточной функции весьма удобно при анализе так называемых структурных схем. Так, например, исходную схему ОУ, согласно уравнению (1.5) можно представить следующим образом (рис.1.4):

Рис.1.4

Данная схема объекта управления, изображенная в виде соединения передаточных функций составляющих ее звеньев, называется структурной схемой ОУ. Структурная схема – это графическое изображение математической модели САУ в виде прямоугольников, которые соответствуют передаточным функциям по входным и выходным сигналам этих прямоугольников.

Пример 1. Найти передаточную функцию звена W1(p) (рис.1.5),

Подвергнем дифференциальное уравнение обратному преобразованию Лапласа, используя теоремы линейности (1.2) и дифференцирования (1.3):

z1'(t) 10z1(t) 5v1(t) Z1(p) p 10Z1(p) 5V1(p).

Преобразуем полученное уравнение:

Z1(p)(p 10) 5V1(p).

Поскольку передаточной функцией называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины, выразим:

p3Y(p) 12.5p2Y(p) 35pY(p) 100Y(p) p2U(p) 14.5pU(p) 70U(p)p2F(p) 12pF(p) 20F(p).

Подвергнем полученное уравнение обратному преобразованию Лапласа, используя теоремы линейности (1.2) и дифференцирования (1.3). Получим дифференциальное уравнение ОУ для функций времени:

y'''(t) 12.5y''(t) 35y'(t) 100y(t) u''(t) 14.5u'(t) 70u(t)

f ''(t) 12f '(t) 20f (t).

1.4.СПОСОБЫ СОЕДИНЕНИЯ ЗВЕНЬЕВ

14

В системах управления встречаются три вида соединений звеньев: последовательное, параллельное и соединение по схеме с обратной связью (встречно-параллельное).

Последовательным называется соединение динамических звеньев, при котором выходная переменная каждого предыдущего звена подается на вход последующего звена:

Из рис.1.6 следует:

Y(p) Yn 1(p) Wn(p) Yn 2(p) Wn 1(p) Wn(p) X p W1(p) ... Wn 1(p) Wn(p)

n

X p Wi(p)

i1

Таким образом, передаточная функция последовательного соединения динамических звеньев равна произведению передаточных функций, составляющих схему:

n

Wпосл(p) Wi (p)

i 1

Параллельным называется соединение, при котором входная переменная всех звеньев одна и та же, а выходные переменные всех звеньев суммируются:

Y1 p

W1(p)

Из рис.1.7 следует:

Y(p) Y1(p) Y2 (p) ... Yn (p) X p W1(p) X p W2 (p) ... X p Wn (p)

n

X p Wi (p)

i1

15

Передаточная функция параллельного соединения динамических звеньев равна сумме передаточных функций:

n

Wпар(p) Wi (p)

i 1

Соединением с обратной связью (встречно-параллельным соединением) называется такое соединение динамических звеньев, при котором сигнал с выхода прямой цепи подается на его вход через звено обратной связи (рис.1.8). Обратная связь может быть положительной (ПОС) и отрицательной (ООС).

W1(p) - звено прямой цепи;

W2(p) - звено цепи обратной связи; X(p) - сигнал обратной связи;

E(p) G(p) X(p) - сигнал рассогласования. Из рис.1.8 следует:

X(p) Y(p)W2(p)

Y(p) E(p)W1(p) G(p) X(p)W1(p) G(p) Y(p)W2(p)W1(p)G(p)W1(p) Y(p)W1(p)W2(p)

Y(p) Y(p)W1(p)W2(p) G(p)W1(p)

Y(p)1 W1(p)W2(p) G(p)W1(p)

где «-» соответствует ПОС; «+» соответствует ООС.

Если W2(p) 1, то структурная схема системы с ОС имеет вид (рис.1.9):

16

Рис.1.9

1.5.ПРАВИЛА ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ

Расположенные рядом сумматоры можно перемещать друг относительно друга в любом порядке, и их действие на схему не изменится.

Два или несколько расположенных рядом узлов можно менять друг относительно друга в любой последовательности.

Не рекомендуется переносить сумматор через узел разветвления и наоборот.

Перенос сумматора через звено в прямом направлении. При переносе сумматора через звено в прямом направлении в цепь переносимого сигнала включается звено с передаточной функцией того звена, через которое осуществляется перенос.

Перенос сумматора через звено в обратном направлении. При переносе сумматора через звено в обратном направлении в цепь переносимого сигнала дополнительно включается звено с передаточной функцией, обратной передаточной функции звена, через которое осуществлен перенос.

Перенос узла через звено в прямом направлении. При переносе узла через звено в прямом направлении в цепь переносимого сигнала дополнительно включается звено с передаточной функцией, обратной передаточной функции звена, через которое осуществлен перенос.

Перенос узла через звено в обратном направлении. При переносе узла через звено в обратном направлении в цепь переносимого сигнала включается звено с передаточной функцией того звена, через которое осуществляется перенос.

Пример. Преобразуем (упростим) структурную схему (рис.1.10) и получим эквивалентную (результирующую) передаточную функцию.

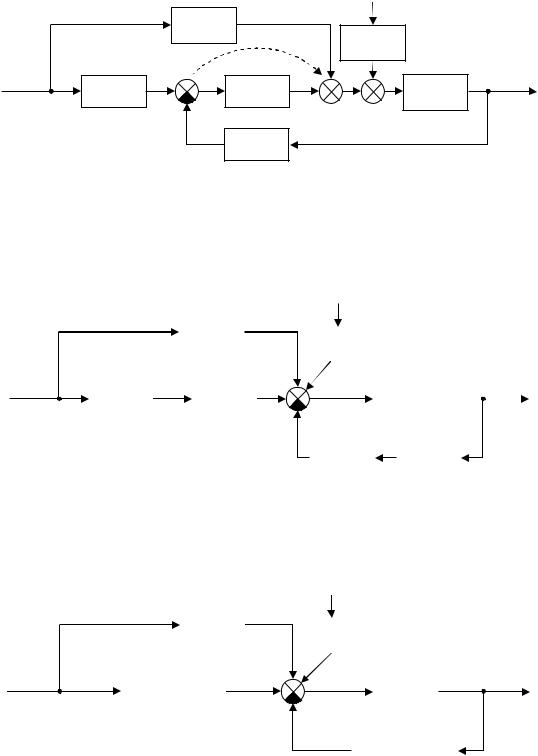
17

W4(p)

Рис.1.10

Перенесем сумматор 1 через звено W2(p) в прямом направлении и объединим с сумматорами 2 и 3. В цепь переносимого сигнала включается звено с передаточной функцией звена W2(p), через которое осуществляется перенос (рис.1.11).

Звенья W1(p) и W2 (p), W2(p) и W4 (p) соединены последовательно, заменим их звеньями с результирующими передаточными функциями, равными произведениям W1(p)W2(p) и W2(p)W4(p) (рис.1.12).

параллельно, результирующая передаточная функция равна их сумме

(рис.1.13).

W6(p) 1. Вычислим:

передаточных функций Wyu(p) и Wyf (p) были одинаковые знаменатели,

1.6.ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ ОДНОКОНТУРНОЙ СИСТЕМЫ МЕЖДУ ПРОИЗВОЛЬНЫМИ ВХОДАМИ

И ВЫХОДАМИ

Пусть САУ имеет следующую структурную схему (рис.1.16):

Рис.1.16

Поскольку звенья с передаточными функциями W1(p), W2(p), W3(p)

входят в прямую цепь регулирования, то передаточные функции

20

Wyg(p) W1(p)W2(p), Wyf (p) W3(p), Wg (p) 1, Wyf (p) W3(p) называют передаточными функциями прямой цепи по задающему и возмущающему воздействиям.

Передаточная функция WРЦ (p), включающая все звенья,

расположенные в прямой цепи и в цепи обратной связи, называется передаточной функцией разомкнутой цепи. В данном случае

WРЦ (p) W1(p)W2(p).

Передаточная функция yg (p) Y(p) называется передаточной

G(p)

функцией замкнутой системы по задающему (регулирующему) воздействию.

функцией замкнутой системы по возмущению.

функцией замкнутой системы по ошибке от задающего воздействия.