4.4. Ряд Фурье для функции с периодом 2π

Ответ на поставленные вопросы дает следующая теорема.

Теорема (необходимое условие разложения функции в тригонометрический ряд)

Если периодическая функция f(x) с периодом 2π, кусочно-непрерывная на [-π; π] разлагается в тригонометрический ряд, т.е.

,

то это разложение единственно и коэффициенты тригонометрического ряда находятся по формулам:

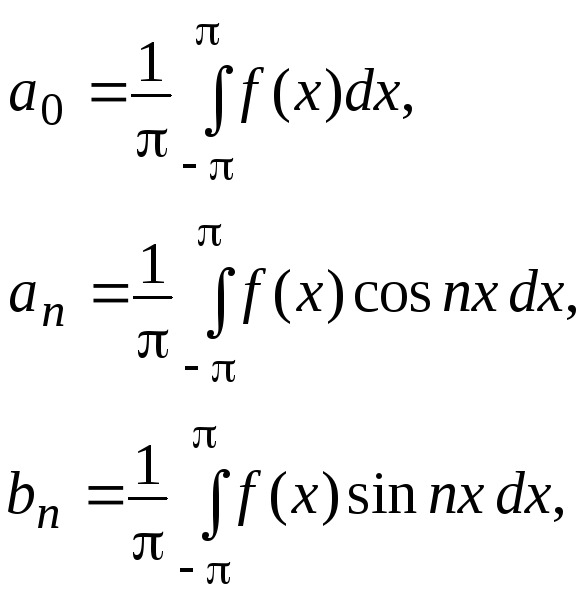
Числа а_о,, а_п,, b_п, при п = 1,2,3,..., определяемые для функции f(x) по приведенным в теореме формулам, называются коэффициентами Фурье для этой функции, а тригонометрический ряд с такими коэффициентами называется рядом Фурье для функции f(x).

Ответ на вопрос, какой должна быть функция f(x), чтобы ее можно было разложить в тригонометрический ряд, дает теорема Дирихле, которая определяет достаточные условия разложимости функции в ряд Фурье.

Теорема Дирихле

Если периодическая функция f(x) с периодом Т = 2π на отрезке [-π; π ] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок [-π; π] можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) сумма ряда S(x) равна f(x), а в точках разрыва функции f(x) сумма ряда равна

(среднему арифметическому предельных значений слева и справа), т.е.

Функция f(x), удовлетворяющая условиям теоремы Дирихле (кроме условия периодичности), называется кусочно-монотонной на отрезке [-π; π ].

Таким образом, для всех точек непрерывности функции справедливо

.

Итак, если периодическая функция f(x) с периодом Т = 2π удовлетворяет условиям теоремы Дирихле, то существует тригонометрический ряд – ряд Фурье функции f(x), суммой которого является рассматриваемая функция f(x). В этом случае говорят, что функция разложима в ряд Фурье.

Заметим, что пределы интегрирования при определении коэффициентов Фурье не обязательно должны быть симметричны относительно начала координат. Длина промежутка интегрирования должна равняться периоду функции. Выбор промежутка интегрирования зависит от свойств функции.

При разложении функции f(x) в ряд Фурье советуем пользоваться следующим алгоритмом:

1) построить график функции f(x) на нескольких периодах;

2) проверить выполнение условий Дирихле для функции f(x);

3) вычислить коэффициенты Фурье но формулам

4) записать разложение функции в ряд Фурье

и указать область, в которой это разложение справедливо.

Заметим, что областью сходимости ряда Фурье к порождающей его функции, является область непрерывности функции f(x).

При вычислении коэффициентов Фурье полезно помнить, что

sin0 = 0, sin nπ =0, cos0 = 1, cos nπ = (-1)^п.

Пример 30

Разложить в ряд Фурье функцию

удовлетворяющую условию f(x + 2π) = f(x).

Решение.

Так как для функции f(x) выполняется условие f(x+2π)=f(x), следовательно, функция является периодической с периодом Т =2π. Построим график функции f(x) (рисунок 3).

Рисунок 3

Функция f(x) на отрезке [-π; π] удовлетворяет условиям Дирихле, т.е. является кусочно-монотонной.

Вычислим коэффициенты Фурье этой функции:

,

.

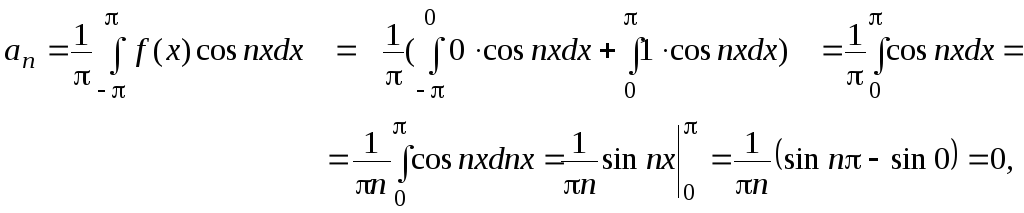
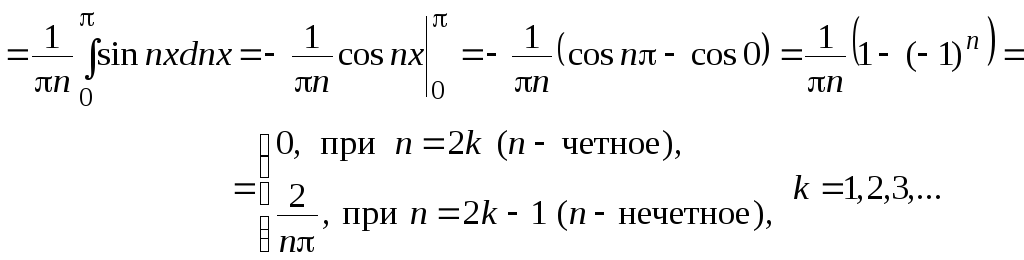Запишем ряд Фурье

Ряд сходится при любых значениях х, но его сумма S(x) совпадает с функцией f(x) в точках непрерывности функции, т.е. для всех х, кроме точек разрыва функции. Данная функция имеет точки разрыва первого рода в точках х = 0,х =± π, х = ±2π,...(это хорошо видно из чертежа), т.е. x-t π, t  Z .В точках разрыва сумма ряда равна

.

Итак, разложение функции в ряд Фурье имеет вид

при .

Заметим, что график суммы ряда Фурье для данной функции совпадает с графиком данной функции в точках непрерывности функции, а в точках разрыва функции сумма ряда равна 1/2 (рисунок 4).

Рисунок 4

4.5. Разложение четных и нечетных функций с периодом Т=2π в ряд Фурье

Отметим важные частные случаи разложения функции в ряд Фурье. Пусть функция f(x) интегрируема на [-π, π] и является четной, т.е. для любых х D(y) выполняется условие –х  D(у) и f(-x) = f(x).

Если f(x) - четная, то произведение четных функций f(x) и cosnx так же четная функция, а произведение четной функции f(x) и нечетной функции sinnx есть функция нечетная. Тогда, учитывая свойства определенного интеграла

можно упростить формулы для вычисления коэффициентов Фурье:

,

,

b_n = =0.

Следовательно, ряд Фурье для четной функции содержит только четные функции - косинусы и записывается в виде

где коэффициенты a₀, a_n вычисляются по формулам

, .

Если функция f(x) интегрируема на [-π. π] и является нечетной, т.е. для любого х  D(y) выполняется условие -х D(y) и f(-x) = -f(x), то произведение нечетных функций f(x) и sin nx: есть функция четная, а произведение нечетной функции f(x) и четной функции cosnx есть функция нечетная. Учитывая приведенное выше свойство определенного интеграла, получим формулы для вычисления коэффициентов Фурье:

,

,

b_n = .

Следовательно, ряд Фурье для нечетной функции содержит только нечетные функции - синусы и записывается в виде

где коэффициенты Ь_п определяются по формуле

b_n = .

Пример 31

Разложить в ряд Фурье функцию f(x), заданную графически (рисунок 5).

Решение.

Из графика видно, что функция является периодической с периодом Т-2π, Так как график функции симметричен относительно начала координат, то функция является нечетной. На отрезке [-π,π] выполняются условия Дирихле, следовательно, функция разложима в ряд Фурье.

Рисунок 5

Так как функция нечетная, то а₀=а_п=0. Для вычисления b_п необходимо функцию задать аналитически:

Вычислим коэффициенты b_п:

Запишем ряд Фурье для функции в точках ее непрерывности

Полученный ряд сходится на всей числовой прямой, его сумма S(x) в точках непрерывности совпадает с функцией f(x)_, а в точках разрыва функции, т.е. при х ≠ tπ, t Z , сумма ряда Фурье

.

Итак, разложение данной функции в ряд Фурье имеет вид:

.

На рисунке 6 построен график суммы S(x) полученного ряда Фурье.

Рисунок 6

4.6. Разложение в ряд Фурье периодических функций с произвольным периодом Т = 2l

Пусть функция f(x) имеет произвольный период Т = 2l и на отрезке [-l,l] удовлетворяет условиям Дирихле. Разложим ее в ряд Фурье.

Рассмотрим для этого вспомогательную функцию. Полагая x=at,получим функцию f(at) с периодом. Выберема так, чтобы период был равен 2π, т.е. . Тогда подстановкаx = at приведет к функции с периодомТ = 2π. Так как удовлетворяет условиям Дирихле, то ее можно представить рядом Фурье в точках ее непрерывности:

,

где

Возвращаясь, как в ряде, так и в формулах коэффициентов Фурье, от новой переменной t к старой переменной х, учитывая, что , аdt =в точках непрерывности функции f(x) получаем

,

где

Заметим, что если в последних формулах положить l = π, то получим формулы для разложения в ряд Фурье функции с периодом Т = 2π.

Если периодическая функция f(x) с периодом Т = 21 является четной, то в точках непрерывности функции f(x) разлагается в ряд косинусов

,

где коэффициенты а₀, а_п определяются по формулам

, .

Если функция f(x) - периодическая с периодом Т=21 является нечетной, то в точках непрерывности функции f(x) разлагается в ряд синусов

где коэффициенты b_n определяются по формуле .

Пример 32

Разложить в ряд Фурье функцию у =|sinx|.

Решение

Построим график данной функции (рисунок 7). Из чертежа видно, что функция у =|sinx| является периодической с периодом Т = π (значит, 2l= π, откуда l=π/2), четной (так как график функции симметричен относительно оси Оу). На отрезке [0, л] функция непрерывна, следовательно, удовлетворяет условиям Дирихле (заметим, что функция является непрерывной и на всей числовой прямой), значит, функция разложима в ряд Фурье, причем в ряд косинусов (так как функция четная).

Рисунок 7

Найдем коэффициенты Фурье:

,

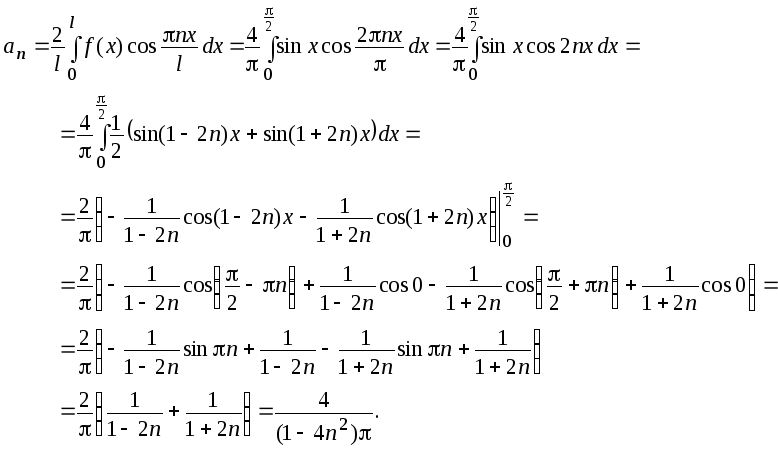Следовательно,

.

Заметим, что графики данной функции и суммы полученного ряда Фурье совпадают на всей числовой оси, так как функция у = |sinx| непрерывна на всей числовой оси.