Тема 4. Тригонометрические ряды Фурье

4.1. Периодические функции и их свойства

В науке и технике часто приходится иметь дело с периодическими процессами: колебательными движениями деталей машин, приборов, движением небесных тел и элементарных частиц, электромагнитными колебаниями и т.д. Математически такие процессы описываются периодическими функциями.

Функция f(x), определенная на всей числовой оси, кроме, может быть, некоторых точек, называется периодической с периодом Т, если существует такое число Т≠0, что для любого значения х из области определения функции выполняется равенство:

f(x + T) = f(x).

Если число Т является периодом функции f(x), то число Т·п при любом целом п так же будет периодом этой функции.

Наименьший из положительных периодов данной функции называют основным периодом функции.

Например, любую константу можно рассматривать как периодическую функцию с каким угодно периодом. Наиболее известными периодическими функциями с периодом Т = 2π являются тригонометрические функции у = sin х, у = cos х..

Свойства периодических функций

1. Сумма, разность, произведение и частное периодических функций с периодом Т есть периодическая функция с тем же периодом.

2. Если функция f(x) имеет период Т, то функция f(a·x) имеет период , гдеа ≠0, а =const.

Например, так как функции y = sinx, y = cosx являются периодическими с периодом Т=2π, то функции y=sinkx и y=coskx также являются периодическими и имеют период . Функцииy = sinkx и у= coskx называют «простыни гармониками».

3. Определенный интеграл от периодической функции по отрезку, который равен периоду, не зависит от положения отрезка интегрирования на оси, т.е. если f(x) = f(x + T), тo.

Геометрически для неотрицательных функций это свойство означает равенство площадей закрашенных областей фигур (рисунок 2).

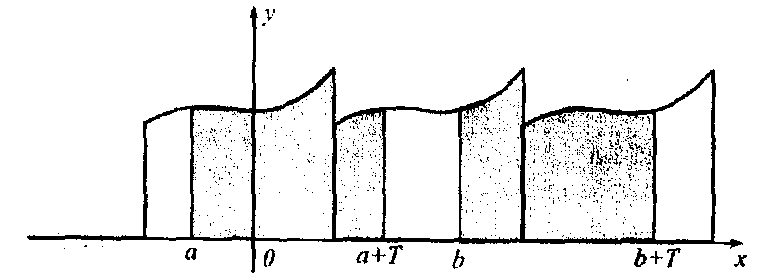
Рисунок 2

4.2. Ортогональные системы функций

Рассмотрим несколько вспомогательных понятий, которые потребуются нам в дальнейшем.

Функции f(x) и φ(х) называются ортогональными на отрезке [а,b], если они определены, интегрируемы на этом отрезке и выполняется равенство

.

Например, рассмотрим функции f(x)= х и на отрезке[0, l]. Они определены и непрерывны на отрезке [0;1]. Найдем определенный интеграл от произведения этих функций по указанному отрезку:

.

Следовательно, функции f(x) = x и ортогональны на отрезке[0,l].

Система функций f,(x), f₂(x),…, f_n (x) называется ортогональной на отрезке [a,b], если любые две различные функции ортогональны, т.е.

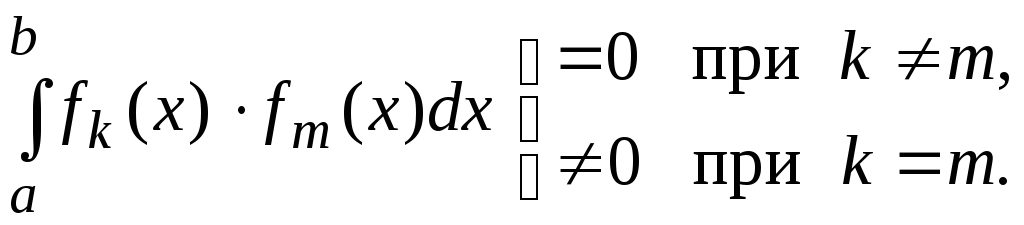
В качестве примера приведем систему {1, cosx, sinx, cos2x , sin2x ,..., cosnx, sinnx,...}, пZ, которая является ортогональной системой функций на отрезке [-π, π], т.е. является ортогональной системой на отрезке, равном периоду этих функций.

4.3. Гармонические колебания. Тригонометрический ряд

Одним, из важнейших понятий в радиоэлектронике являются электрические колебания. Это колебания напряжения, тока, заряда. Например, радиоволны представляют собой колебания электромагнитного поля. Гармоническим колебанием будем называть любой процесс, который описывается периодической функцией с периодом

или, что равносильно, функцией вида

.

Эту функцию называют синусоидальной или гармоникой; А - амплитуда колебания, это наибольшее значение размаха колебания; ω -угловая частота, показывает, сколько раз данное периодическое явление повторится за 2π (единицу времени); φ - начальная фаза гармонического колебания.

Если мы сложим периодические функции

частоты которых ω, 2ω,…, kω,… кратны наименьшей из них, а периоды соответственно равны , то в результате получим функцию

которая также является периодической с периодом Т, но будет значительно отличаться от синусоидальной функции.

Оказывается, что если взять бесконечное множество простых гармоник, то любую периодическую функцию, с определенными, правда, свойствами, можно представить в виде их суммы или, как говорят, в виде тригонометрического ряда.

Тригонометрическим рядом называется функциональный ряд вида

=.

Числа а_п и b_n, где n=1,2,3,..., называют коэффициентами ряда. Свободный член (нулевую гармонику) записывают в виде для единообразия последующих формул.

Для изучения сложного колебания, описываемого функцией f(x), периодической с периодом Т=2π, можно представить его в виде суммы простых гармонических колебаний, т.е. разложить в функцию в тригонометрический ряд

.

Поставленная задача требует решения трех вопросов:

1. При каких условиях периодическую функцию f(x) с периодом Т можно представить в виде тригонометрического ряда?

2. Единственно ли это разложение?

3. Как вычислить коэффициенты этого ряда?

Мы начнем с решения последних двух вопросов.