1.2 Математическая модель и формулы
“Ядром” центральных композиционных планов является полный факторный эксперимент (ПФЭ) 1-го порядка типа 2 при К<5, либо 2 при К≥5.
Центральными их называют вследствие симметричности относительно центра плана. Композиционными называют потому, что они компонуются путем добавления определенного количества опытов к плану 1-го порядка,
поэтому если линейное уравнение плохо описывает технологический процесс (т.е. линейное уравнение регрессии оказалось неадекватным), то не надо проводить весь эксперимент заново, достаточно добавить несколько опытов, т.е. достроить план до плана 2-го порядка.[1]
1. к точкам ПФЭ планов 1-го порядка добавить 2К «звездных» точек, расположенных на координатных осях факторного пространства на одинаковом расстоянии от центра плана. Эту величину α называют «звездное плечо (α=1,41)
2. увеличить число опытов в центре плана n0.
Число опытов в матрице композиционного плана при К факторах составит [1]:
,
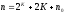при К<5 (1)
,
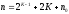при К≥5 , (2)
где К - количество факторов;
2К – звездная точка;
2 - основа плана 1-го порядка;
n – количество опытов;
n0 – количество параллельных опытов в центре плана.
Значениями факторов в кодированном виде будут координаты вершин областей факторного пространства и координаты «звездных» точек.
Полученная матрица не ортогональна, поскольку [1]
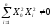(3)
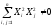(4)
Композиционные планы легко приводится к ортогональным выбором соответствующего «звездного» плеча и преобразованием столбцов Xi², при этом достаточно обратить ту часть, которая связана со столбцами X0 и Xi², т.е. с коэффициентами b0 и bii. Ортогонализацию столбцов Xi² между собой
производят изменением количества опытов в центре плана (n0), вследствие чего изменяется длина «звездного» плеча α. Обычно n0 задается исследователем, а α находится по таблице.
Ортогонализацию столбцов между Хi и Хi² обычно достигается преобразованием квадратичных столбцов по формуле
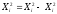(5)
или
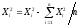, (6)
где Xi² - текущее значение;
Xi² - среднее значение.
Таким
образом получена ортогональная матрица,
которая не требует пересчета коэффициентов
bi
после исключения незначимых факторов.
Получим уравнение регрессии, которое соответствует преобразованной матрице:
(7)
Преобразуем b0 для процесса:
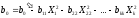(8)
В силу ортогональности матрицы планирования все коэффициенты регрессии определяются независимо друг от друга по формуле:
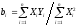(9)
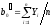(10)
и определяем дисперсию коэффициентов bi
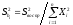(11)
Для вычисления дисперсии воспроизводимости применяется либо классический метод, если проведены параллельные опыты по всей матрице или другой более простой: можно в какой либо точке матрицы, (чаще всего в центре плана) провести несколько параллельных опытов.
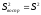(12)
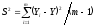, (13)
где m – количество параллельных опытов,(m = 4)
Yi – текущее значение,
Y – среднее значение (мат. ожидание)
1. Проверяем коэффициенты на значимость по критерию Стьюдента:
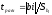(14)
Если tpасч. > tтабл., коэффициент значим.
2. Проверка на адекватность проводится по критерию Фишера, составляя отношение дисперсий [1]
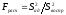(15)
где S²ад. – дисперсия адекватности, вычисляется по формуле:
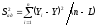, (16)
где Yi – среднее значение,
Yi – расчетное значение,
n – количество опытов,
L – количество значимых коэффициентов,(L = 8)
fч = n – L, (17)
fз = m – 1, (18)
где fч – степень свободы числителя,
fз – степень свободы знаменателя.
Если Fp < Fтабл., то уравнение адекватно [1]
