
- •Вариант 1 Часть1
- •Часть 2
- •Дополнительные задачи
- •Часть 2: 1. А) е2–3; б). 2..; б). 3. 4π. 4. 384 м. 5. 324ρg. 6.8дж Вариант 2 Часть1
- •Часть 2
- •Дополнительные задачи
- •Вариант 3 Часть1
- •Часть 2
- •Дополнительные задачи
- •Часть2. 1 а)б)3πа2/2 2. А)ln3–0,5 б)12. 3. 24π. 4. 150кг 5. 2γаb2/3. 6. 135 дж вариант 4 Часть1
- •Часть 2
- •Дополнительные задачи
- •Вариант 5 Часть1
- •Часть 2
- •Вариант 6 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Часть 2. 1. А)4; б)πа2/4 2. А) 134р/27 ≈ 4,962р; б) 8а3. 39,6π. 4. 1296 5. 11300g6. Вариант 7 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Вариант 8 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Часть 2. 1. А) 36 б) πа2/2 2. А)б)3. 4. 3 сек 5.6,4g
- •Вариант 9 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Вариант 10 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Вопросы к защите
Часть 2
Построить фигуру, ограниченную линиями, и найти ее площадь:
а)
![]() ,
у
= 0, у
= 5 –х;
б)
,
у
= 0, у
= 5 –х;
б)
![]() вне r
= a,
а
> 0.
вне r
= a,
а
> 0.
а) Найти длину дуги кривой у = ех между точками (0, 1) и (1, е). Указание: в качестве независимой переменной взятьу. б) Найти длину дуги кардиоиды
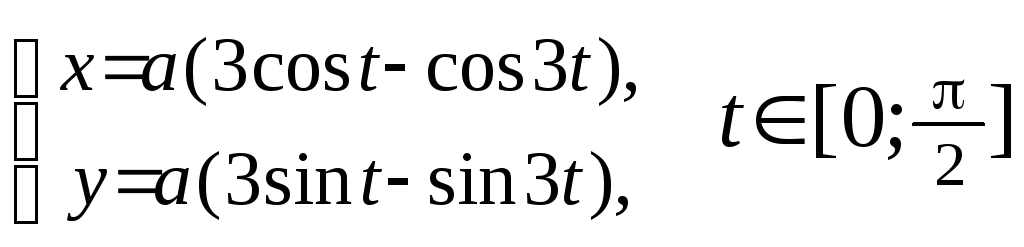 .
.Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями у = tgx, y = ctgx, x =
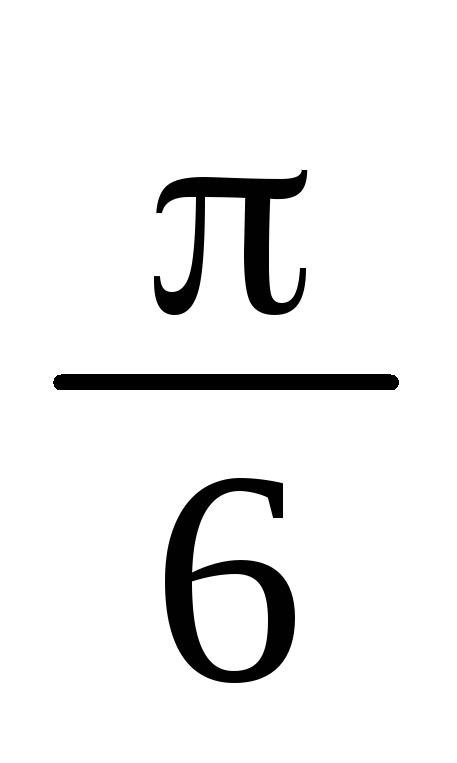 .
.Скорость тела, брошенного вертикально вверх с начальной скоростью v0, с учетом сопротивления воздуха дается формулой
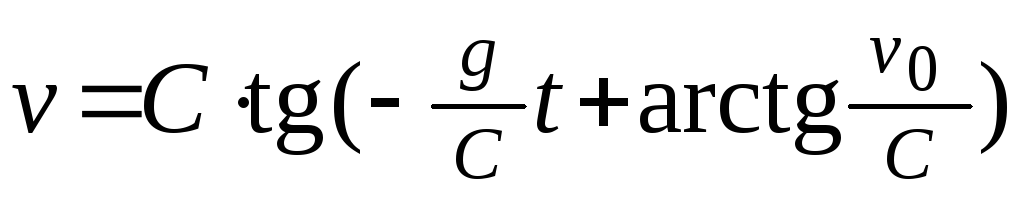 ,
гдеt
– протекшее время, g
– ускорение свободного падения, С
– постоянная. Найти высоту поднятия
тела.
,
гдеt
– протекшее время, g
– ускорение свободного падения, С
– постоянная. Найти высоту поднятия
тела.Вычислить силу давления жидкости с плотностью на вертикальный эллипс с осями 2а и 2b, центр которого погружен в жидкость на уровень h (h b), причем большая ось 2а эллипса параллельна поверхности жидкости.
Тяжелая цепь длиной 100 м поднимается, навиваясь на ворот. Найдите работу силы тяжести при поднятии цепи, пренебрегая размерами ворота, если погонный метр цепи весит 40 кг.
Дополнительные задачи
Вычислить интеграл
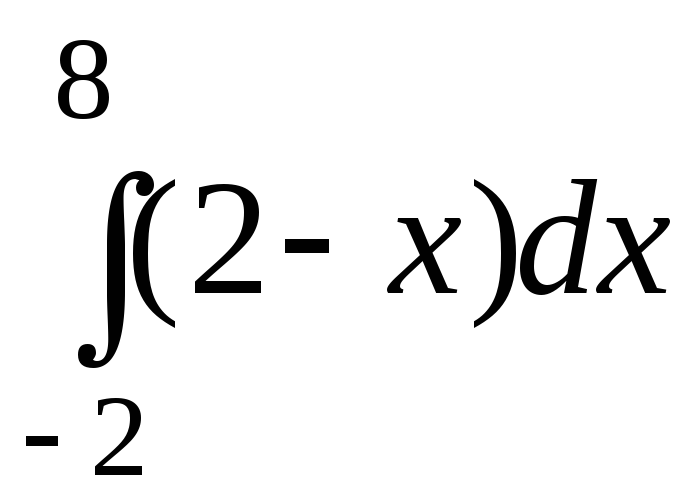 ,
рассматривая его как предел интегральной
суммы.
,
рассматривая его как предел интегральной
суммы.Оценить интеграл
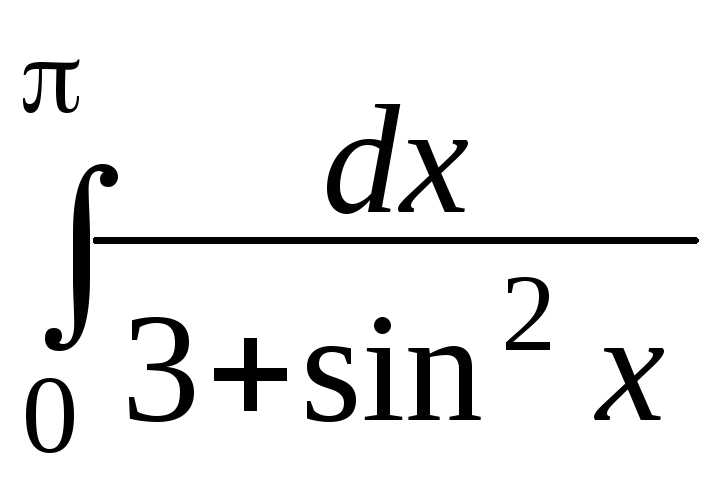 .
.Исходя из геометрического смысла определенного интеграла, найти: а)
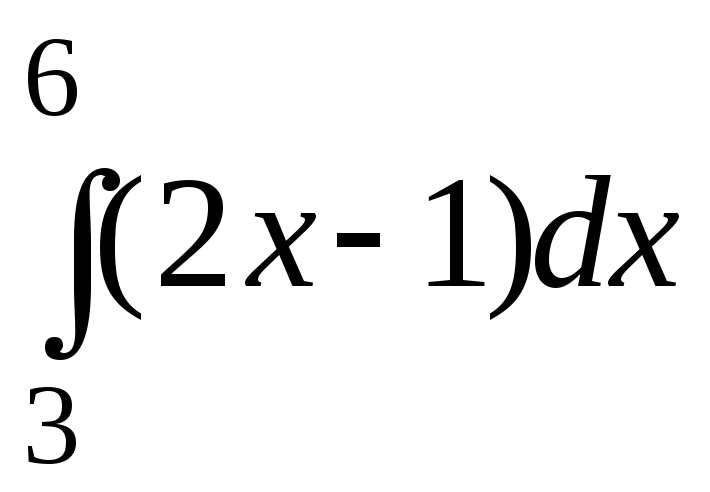 ;
б)
;
б)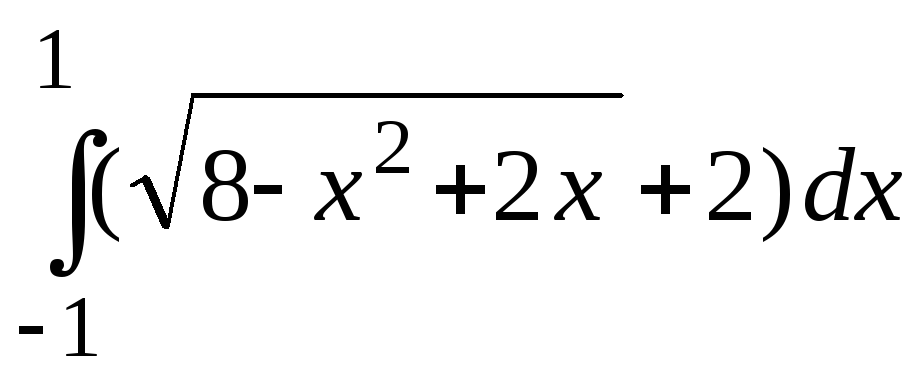 .
.Исследовать сходимость интеграла
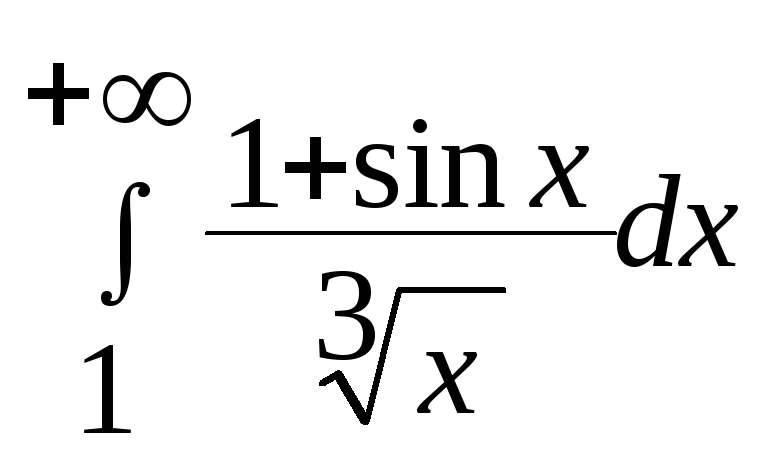 .
.Вычислить
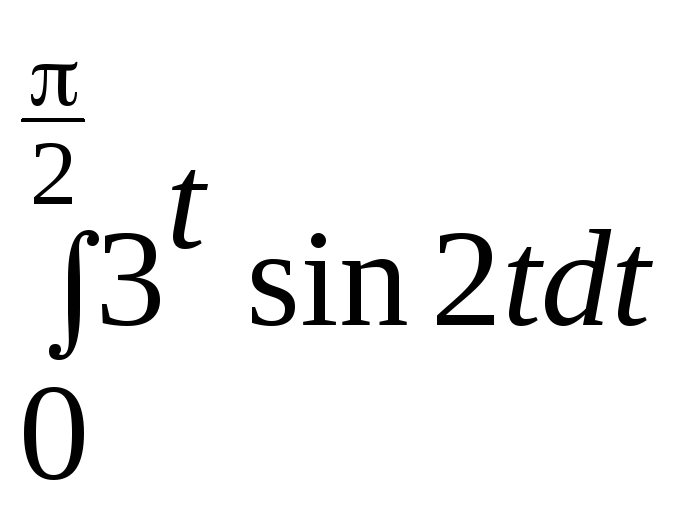 .
.Найти площадь петли декартова листа
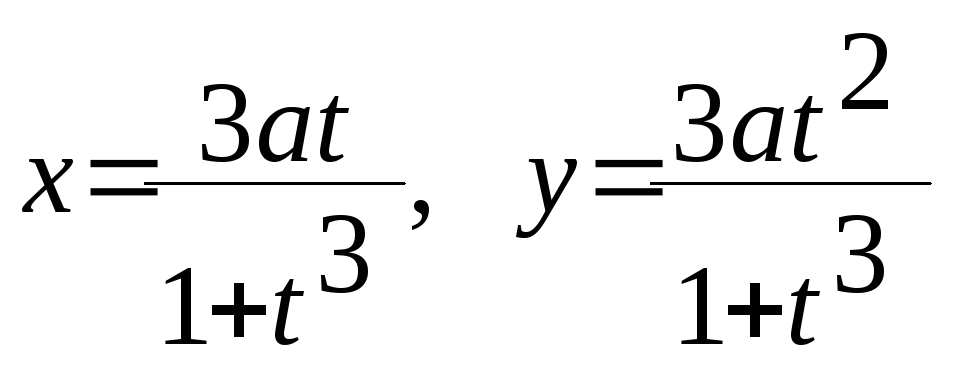 ,
0
t
< +.
,
0
t
< +.Доказать, что дуги линий
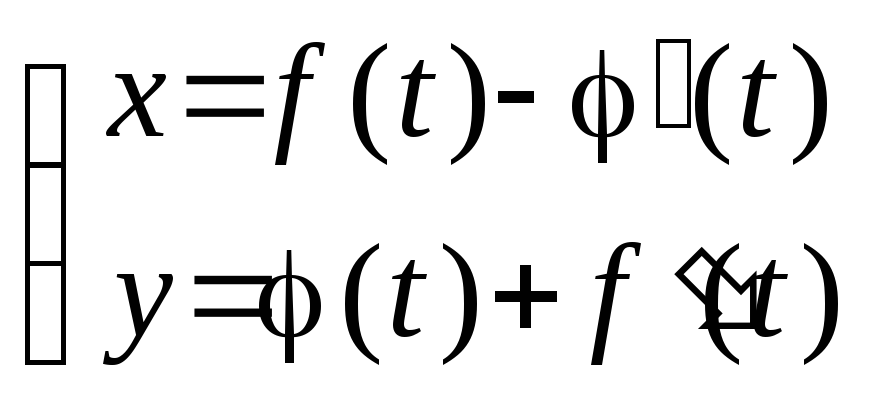 и
и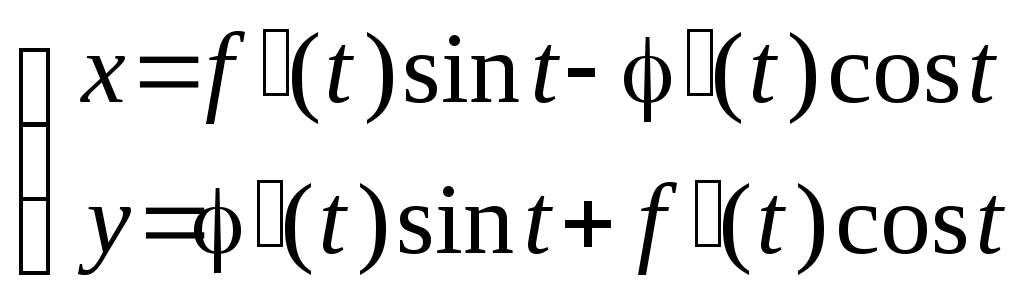 ,
соответствующие одному и тому же
интервалу изменения параметраt,
имеют равные длины.
,
соответствующие одному и тому же
интервалу изменения параметраt,
имеют равные длины. /4б/ Фигура, ограниченная осью ОХ и одной аркой циклоиды х = а(t – sint), y = a(1 – cost), вращается вокруг оси ОУ. Найти объем тела вращения.
Найти массу стержня длины 100 см с переменной плотностью (х)=
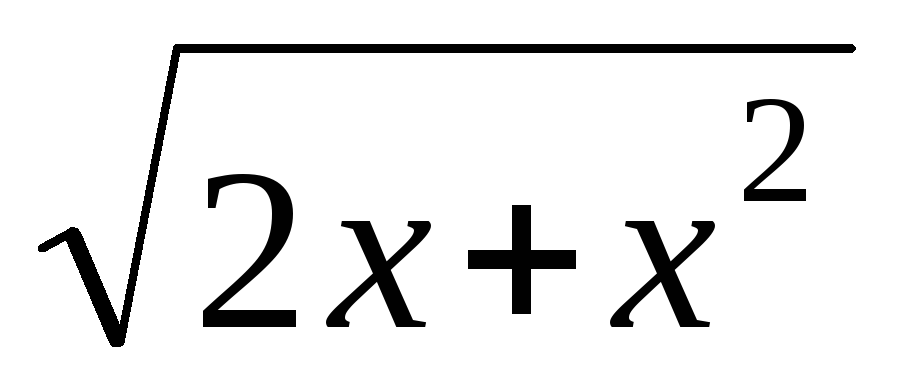 .
.
ОТВЕТЫ. Часть 1. 1. а) нет; б) да; в) нет.
2.. 0 3. а)
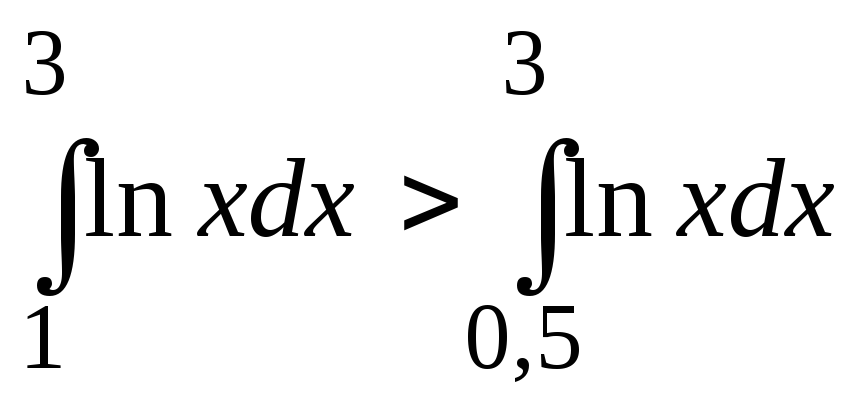 ;
б).
;
б).
![]() 4.
4.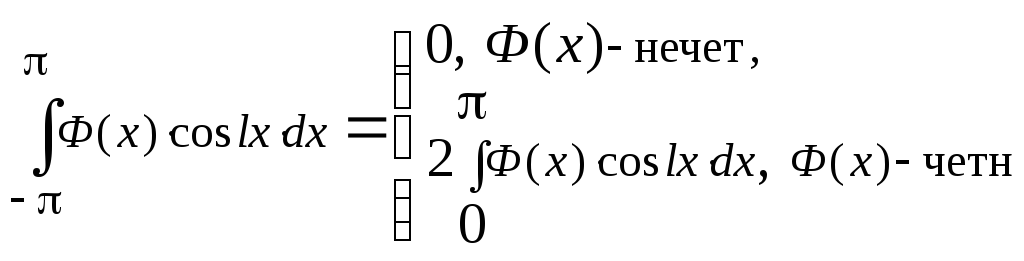 ,
,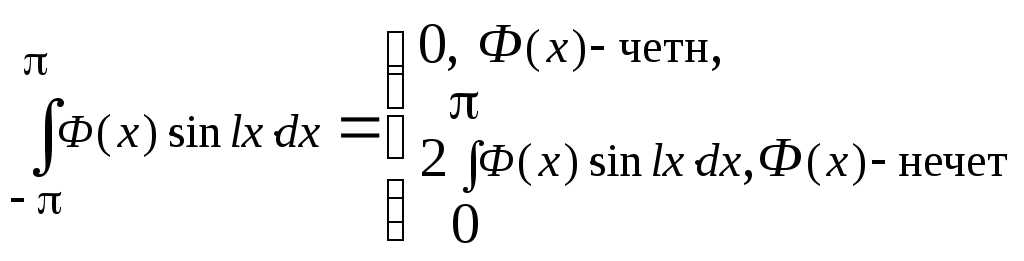 .
5. а)
.
5. а)![]() б) 0 в) 0,25 г)
б) 0 в) 0,25 г)![]() д)(е–1–1)/3 е)ln2
ж)
д)(е–1–1)/3 е)ln2
ж)![]() з)
з)![]() 6.
6.![]() 7.а) расходится б) 1–ln2
Часть 2. 1. а) 32/3 б)
7.а) расходится б) 1–ln2
Часть 2. 1. а) 32/3 б)![]() 2. а)
2. а)![]() б)6а3.
б)6а3.![]() 4.
4.![]() 5.аbhgγ
5.аbhgγ
6. –200000gкг.м.
Вариант 10 Часть 1
Используя теорему существования определенного интеграла, установить, существует ли определенный интеграл от заданной функции по указанному промежутку:
а)
g(x)
= (x+4)cos
x,
![]() ,
б)
,
б)![]() ,
в)у(х)
= х2
+ 3х,
(–;
1]
,
в)у(х)
= х2
+ 3х,
(–;
1]
Используя одно из свойств определенного интеграла, упростить вычисление интеграла
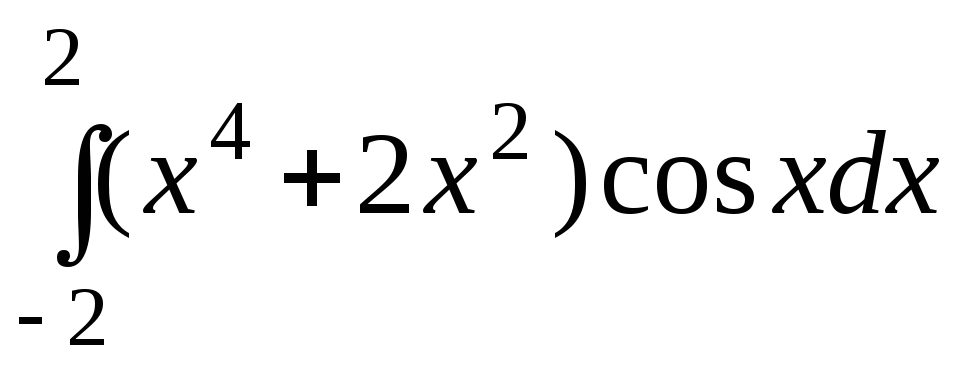 .
.Не вычисляя, определить, какой из интегралов больше:
а)
![]() или
или
![]() ;
б)
;
б)
![]() или
или
![]() .
Ответ обосновать.
.
Ответ обосновать.
4. Чему равны
![]() и
и
![]() ,
если f(х)
- четная функция; нечетная функция?
,
если f(х)
- четная функция; нечетная функция?
5. Вычислить: а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ,
,
д)![]() ,
е)
,
е)![]() ,
ж)
,
ж)
![]() ,
з)
,
з)
![]() .
.
6. Вычислить
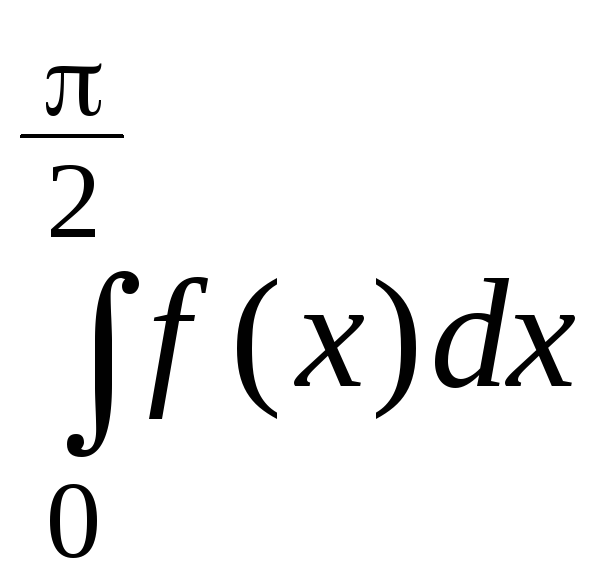 ,
если
,
если
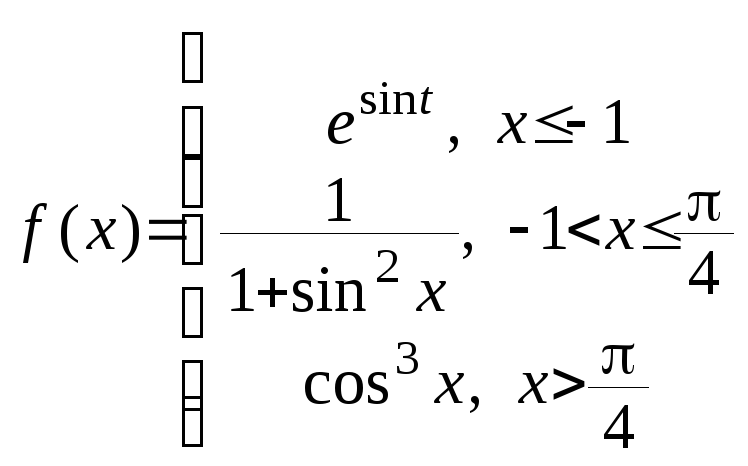 .
.
7. Вычислить интегралы, или установить их расходимость:
а)
![]() ,
б)
,
б)
![]() .
.
Часть 2
Построить фигуру, ограниченную линиями, и найти ее площадь:
а)
![]()
![]() б)
б)
![]() ,
r
= a,
,
r
= a,
![]() .
.
2. а) Найти периметр
фигуры, ограниченной линиями:
![]() Указание: в качестве независимой
переменной взятьу.
Указание: в качестве независимой
переменной взятьу.
б) Найти длину
дуги трактрисы: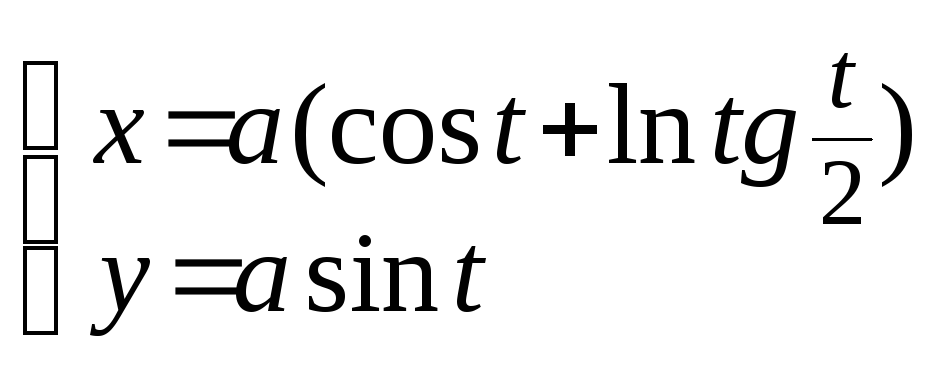 от точки (0; а)
до точки (b;
с).
от точки (0; а)
до точки (b;
с).
Найти объем тела, полученного вращением вокруг оси OY фигуры, ограниченной линиями
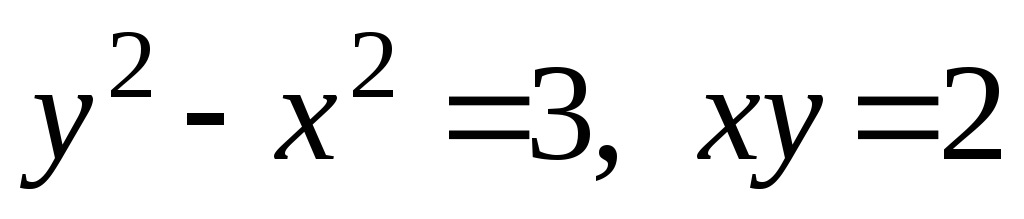 (x,
y
0) и y
= 3.
(x,
y
0) и y
= 3.Ракетный снаряд поднимается вертикально вверх. Считая, что при постоянной силе тяжести ускорение ракеты за счет уменьшения ее веса растет по закону
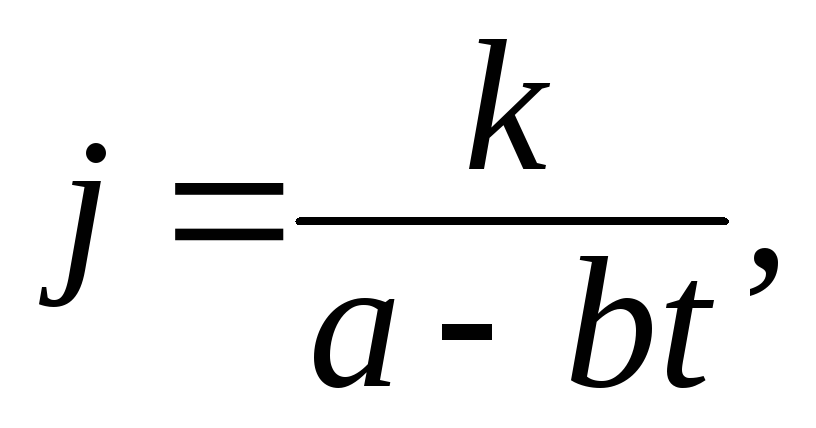
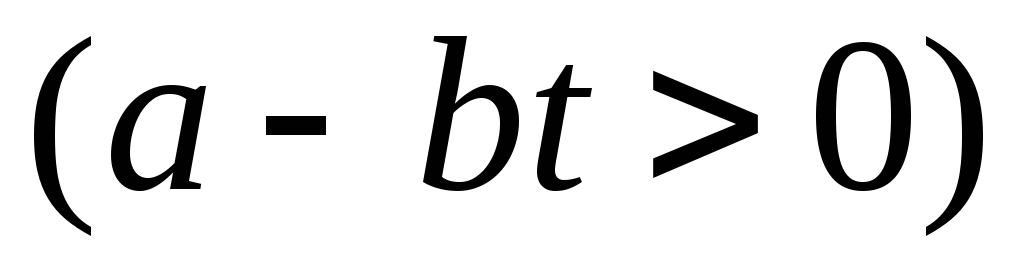 ,
найти скорость ракеты в момент времениt1,
если ее начальная скорость равна нулю.
,
найти скорость ракеты в момент времениt1,
если ее начальная скорость равна нулю.Найти силу давления жидкости с плотностью , заполняющей круговой цилиндр, на его боковые стенки, если радиус основания цилиндра R, высота Н.
Какую работу надо затратить, чтобы тело массы m поднять с поверхности Земли, радиус которой R, на высоту h? Чему равна эта работа, если тело удаляется на бесконечность? (Сила, действующая на тело массойm, равна
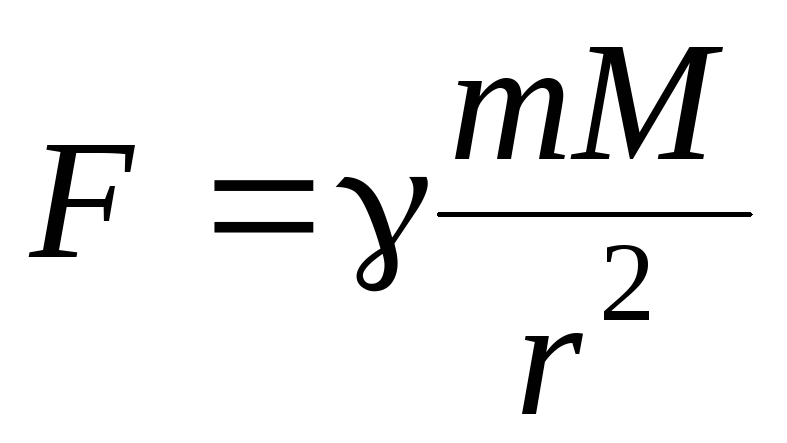 ,
гдеr- расстояние от
центра Земли; М - масса Земли,–
гравитационная постоянная).
,
гдеr- расстояние от
центра Земли; М - масса Земли,–
гравитационная постоянная).
