
- •Вариант 1 Часть1
- •Часть 2
- •Дополнительные задачи
- •Часть 2: 1. А) е2–3; б). 2..; б). 3. 4π. 4. 384 м. 5. 324ρg. 6.8дж Вариант 2 Часть1
- •Часть 2
- •Дополнительные задачи
- •Вариант 3 Часть1
- •Часть 2
- •Дополнительные задачи
- •Часть2. 1 а)б)3πа2/2 2. А)ln3–0,5 б)12. 3. 24π. 4. 150кг 5. 2γаb2/3. 6. 135 дж вариант 4 Часть1
- •Часть 2
- •Дополнительные задачи
- •Вариант 5 Часть1
- •Часть 2
- •Вариант 6 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Часть 2. 1. А)4; б)πа2/4 2. А) 134р/27 ≈ 4,962р; б) 8а3. 39,6π. 4. 1296 5. 11300g6. Вариант 7 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Вариант 8 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Часть 2. 1. А) 36 б) πа2/2 2. А)б)3. 4. 3 сек 5.6,4g
- •Вариант 9 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Вариант 10 Часть 1
- •Часть 2
- •Дополнительные задачи
- •Вопросы к защите
Дополнительные задачи
Вычислить интеграл
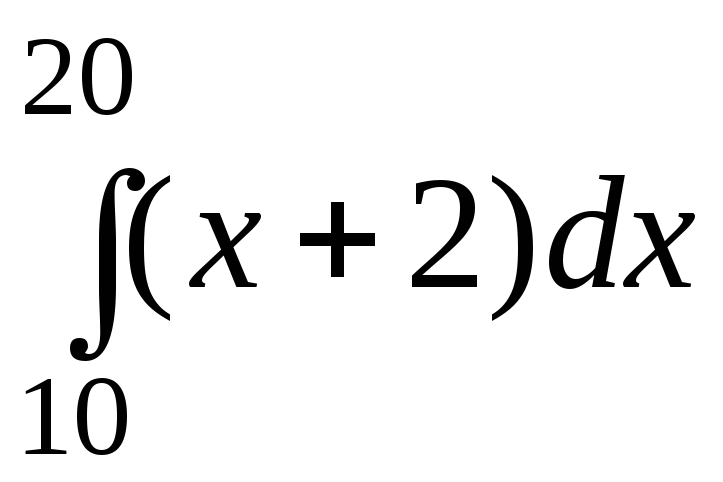 ,
рассматривая его как предел интегральной
суммы.
,
рассматривая его как предел интегральной
суммы.Оценить интеграл
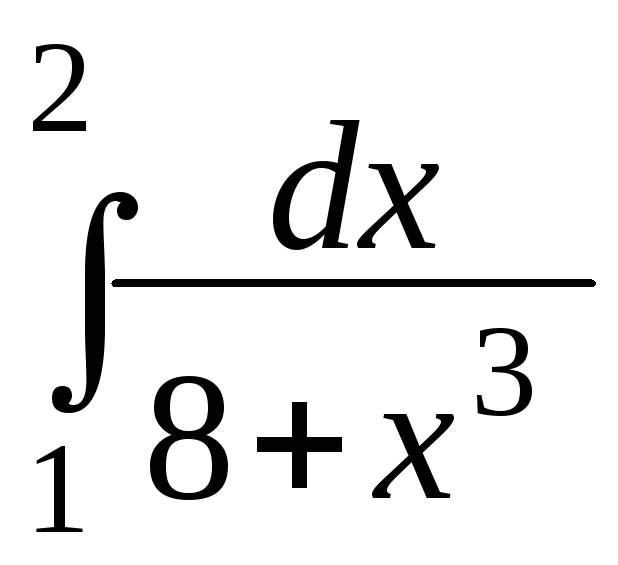 .
.Исходя из геометрического смысла определенного интеграла, найти: а)
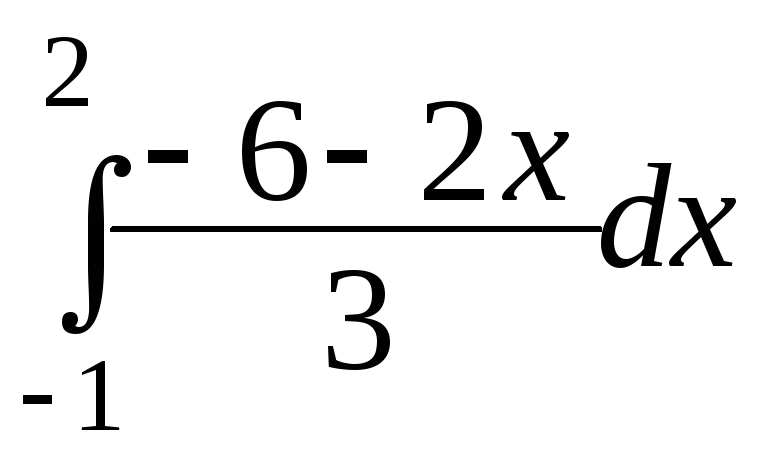 ,
б)
,
б)
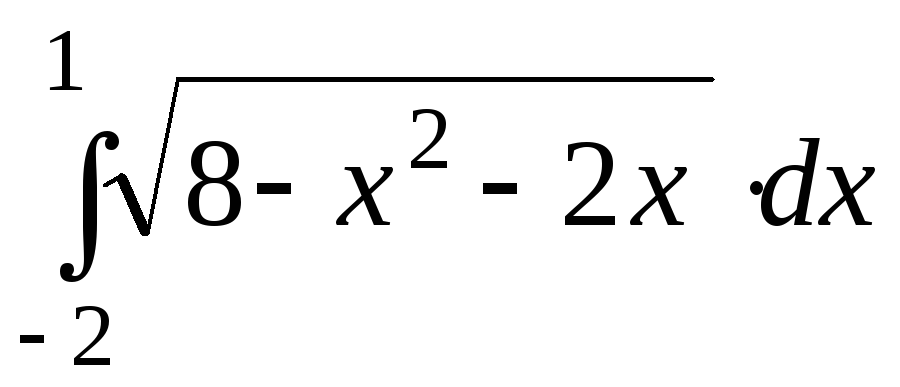 .
.Исследовать сходимость интеграла
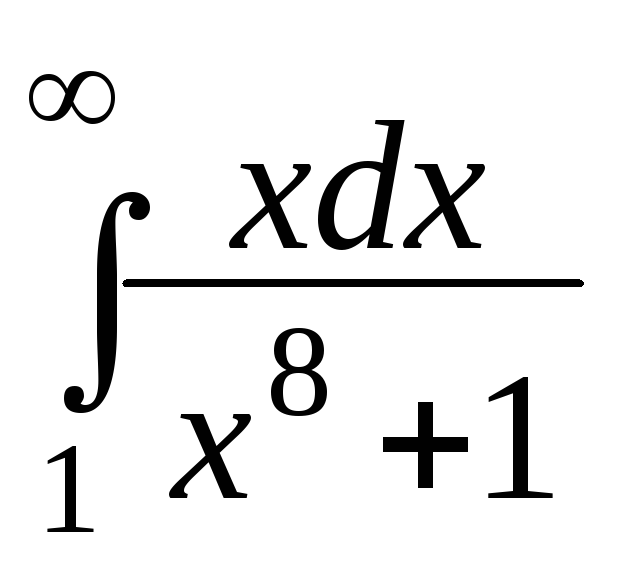 .
.Вычислить
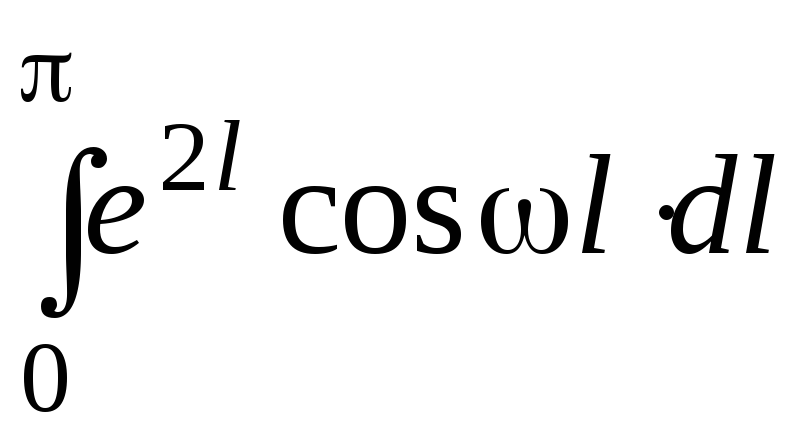 .
.В каком отношении парабола y2=2х делит площадь круга
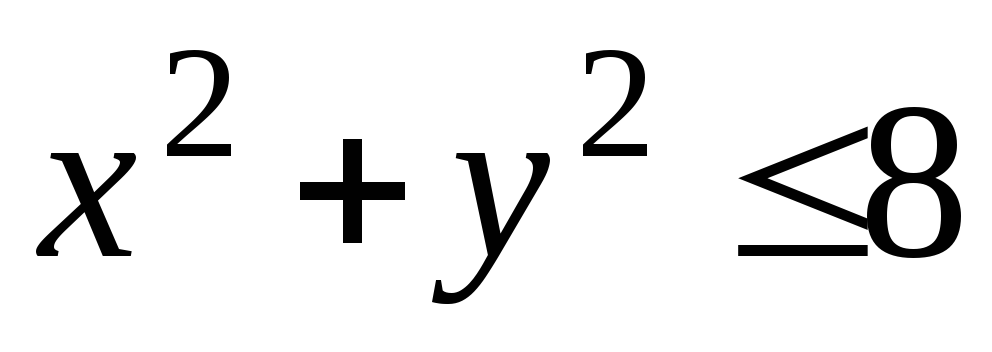 ?
?Найти длину линии, заданной уравнением
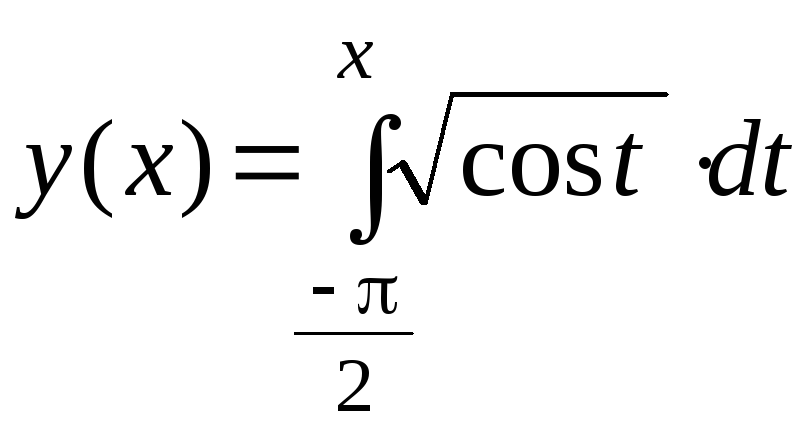 ,
,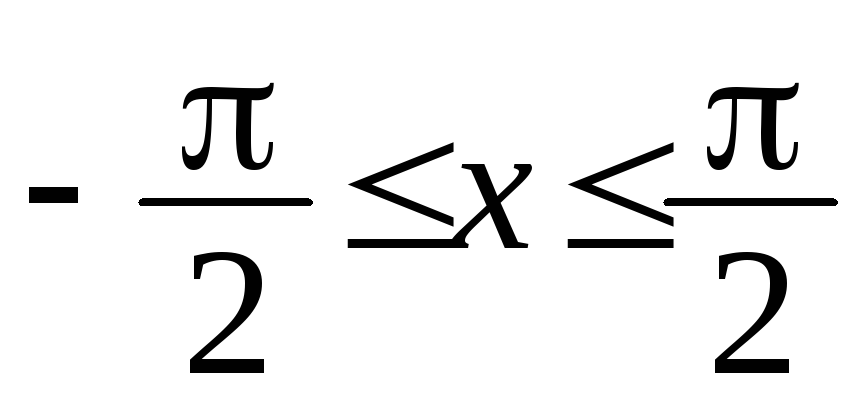 .
.Вычислить объем тела, ограниченного поверхностью бесконечного веретена, образованного вращением линии
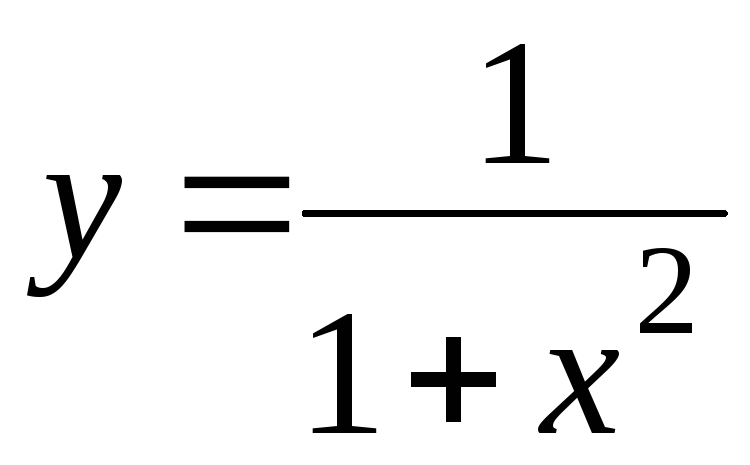 вокруг ее асимптоты.
вокруг ее асимптоты.Цилиндр с подвижным поршнем диаметра Д = 20 см и длины l = 80 см заполнен паром при давлении Р = 10 кГ/см2. Какую работу надо затратить, чтобы при неизменной температуре (изотермический процесс, когда PV = P0V0) объем пара уменьшить в два раза?
ОТВЕТЫ. Часть1. 1. а) да; б)нет; в) нет.
2. 0 3. а)![]() ;
б)
;
б)![]()
4.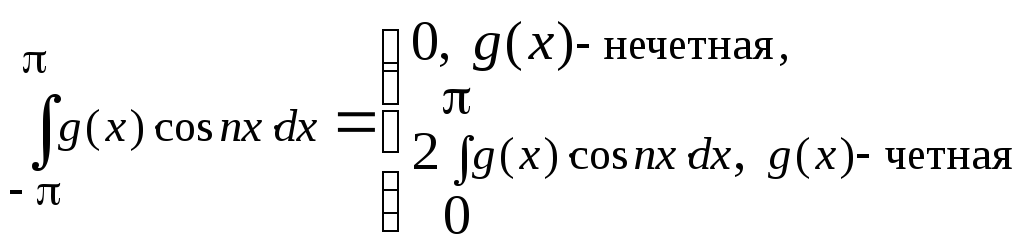 ,
,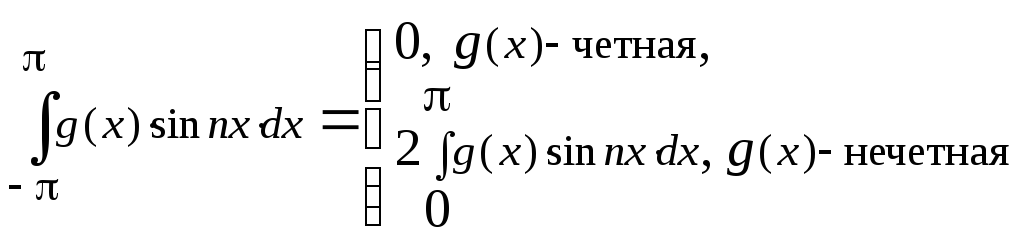 .
.
5. а)11/3 б)![]() в)
в)![]() г)2–π/2 д)
г)2–π/2 д)![]() е)
е)![]() ж)18ln9–104/9
ж)18ln9–104/9
з)
![]() 6.ln8–7/3–4cos4+4cos2
7. а)
6.ln8–7/3–4cos4+4cos2
7. а)![]() б) расходится
б) расходится
Часть 2. 1. А)4; б)πа2/4 2. А) 134р/27 ≈ 4,962р; б) 8а3. 39,6π. 4. 1296 5. 11300g6. Вариант 7 Часть 1
Используя теорему существования определенного интеграла, установить, существует ли определенный интеграл от заданной функции по указанному промежутку: а) f(x) = cosx + 2sinx,
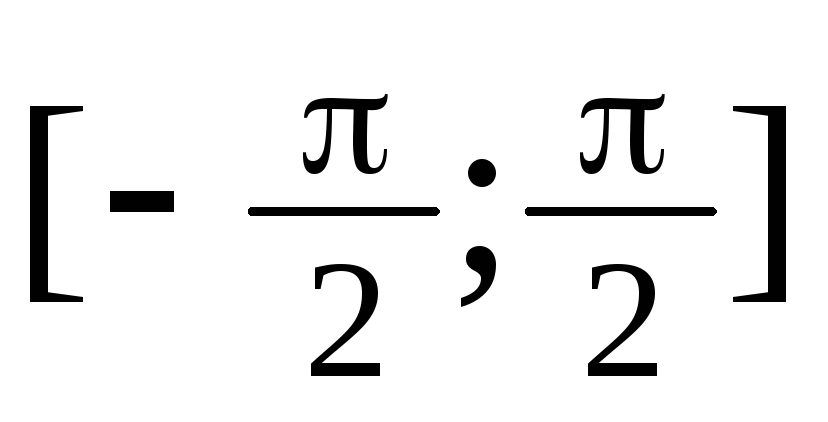 б)
б)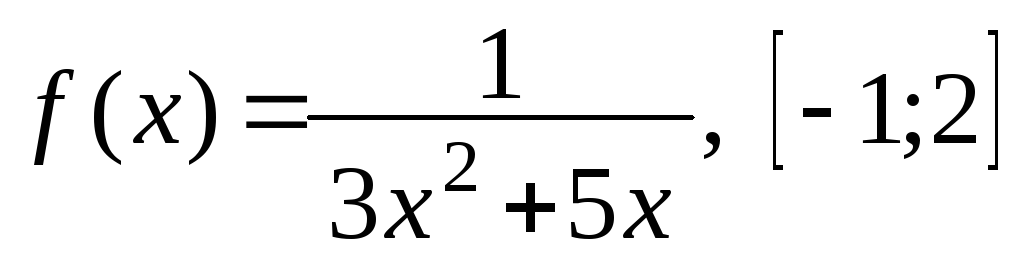 ,
в)
,
в)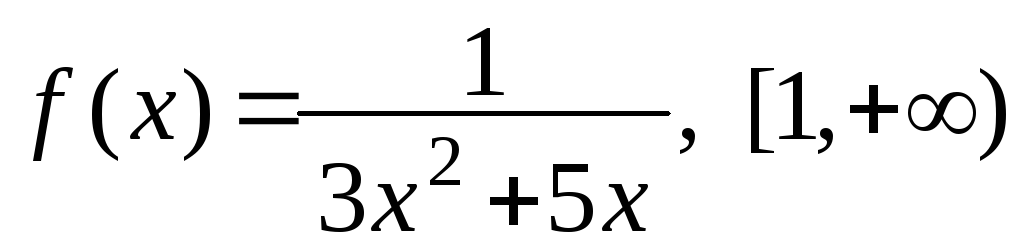
Используя одно из свойств определенного интеграла, упростить вычисление интеграла
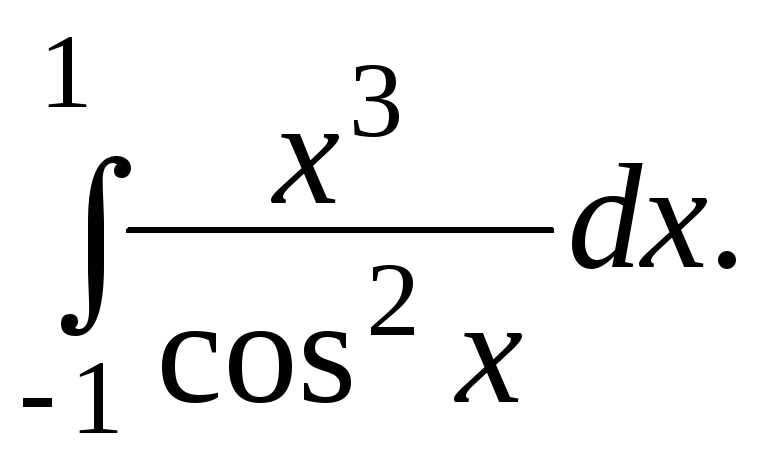
Не вычисляя, определить, какой из интегралов больше:
а)
![]() или
или
![]() ;
б)
;
б)
![]() или
или
![]() .
Ответ обосновать
.
Ответ обосновать
Чему равны
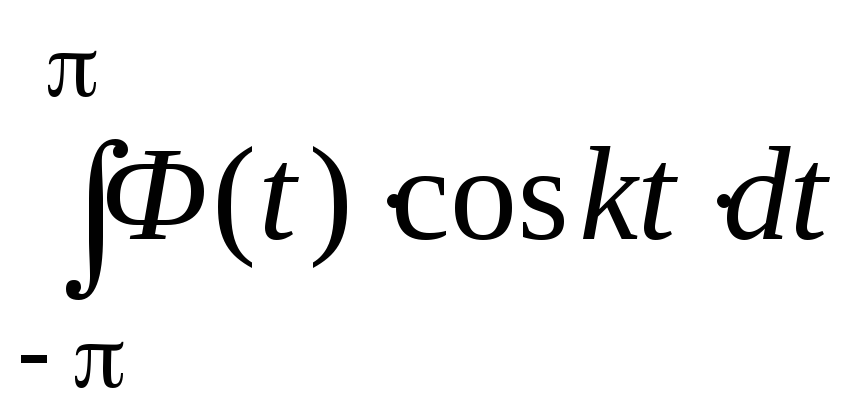 и
и
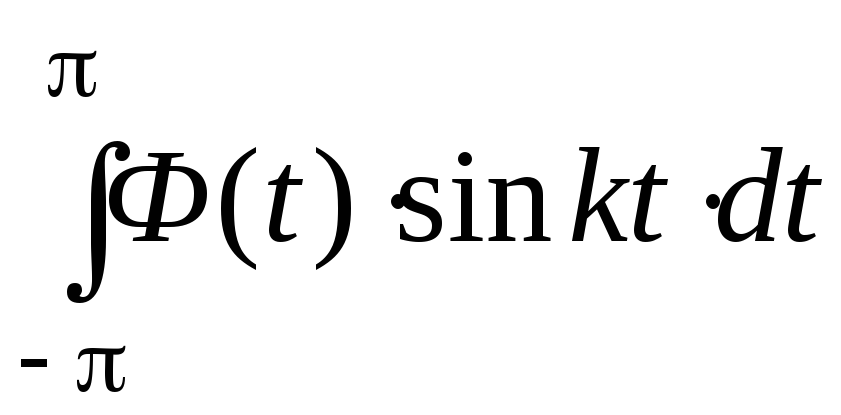 ,
если Ф(х)-
четная функция; нечетная функция?
,
если Ф(х)-
четная функция; нечетная функция?Вычислить: а)
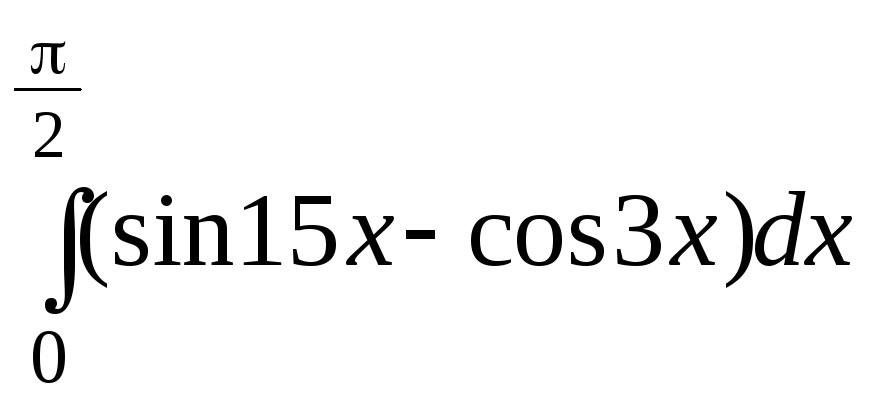 ,
б)
,
б)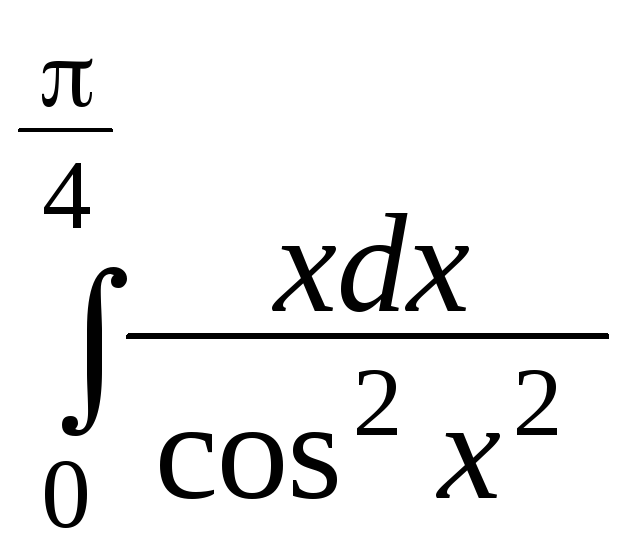 ,
в)
,
в)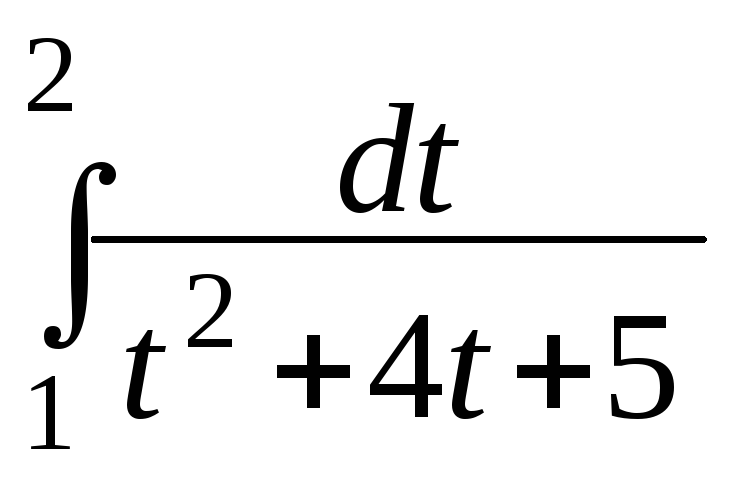 ;
г)
;
г)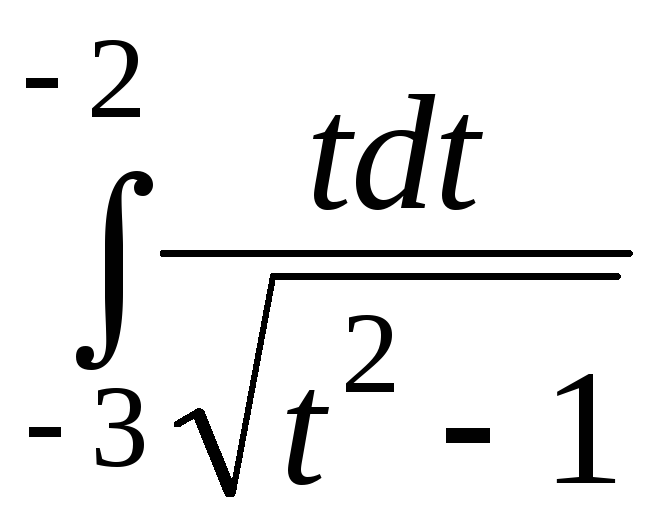 ;
;
д)
![]() ;
е)
;
е)![]() ;
ж)
;
ж)![]() ;
з)
;
з)
![]() .
.
Вычислить
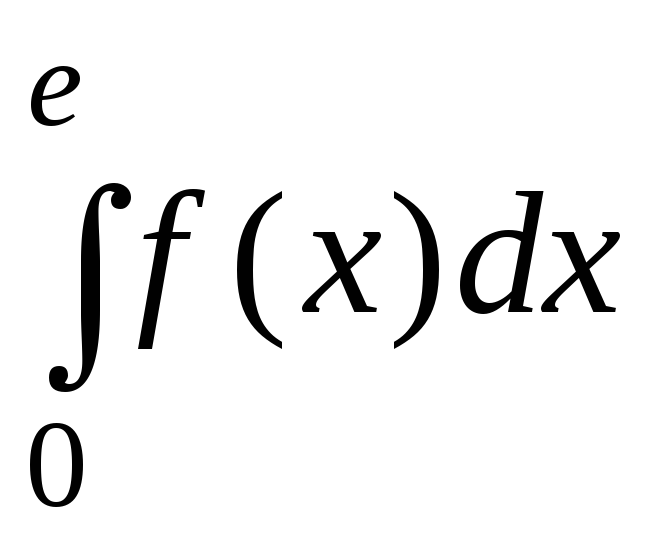 ,
если f(x)
=
,
если f(x)
=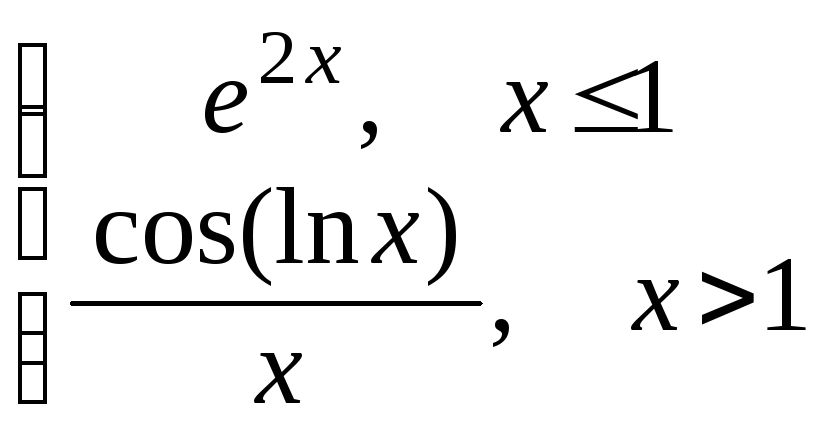 .
.Вычислять интегралы, или установить их расходимость:
а)
![]() ,
б)
,
б)
![]() .
.
Часть 2
Построить фигуру, ограниченную линиями, и найти ее площадь:
а)
![]() ,
,
![]() ,
,
![]() ;
б)
;
б)
![]() , а
> 0.
, а
> 0.
а) Найти длину цепной линии
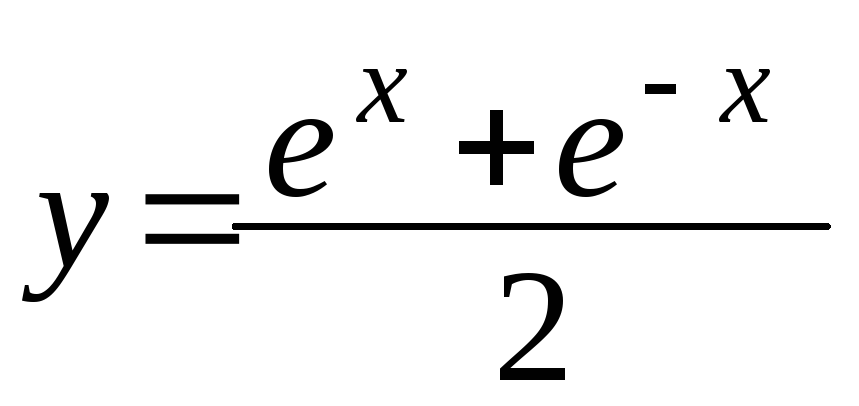 на отрезке [0; а].
на отрезке [0; а].
б) Найти длину
астроиды
![]() .
.
Фигура, ограниченная дугой эллипса
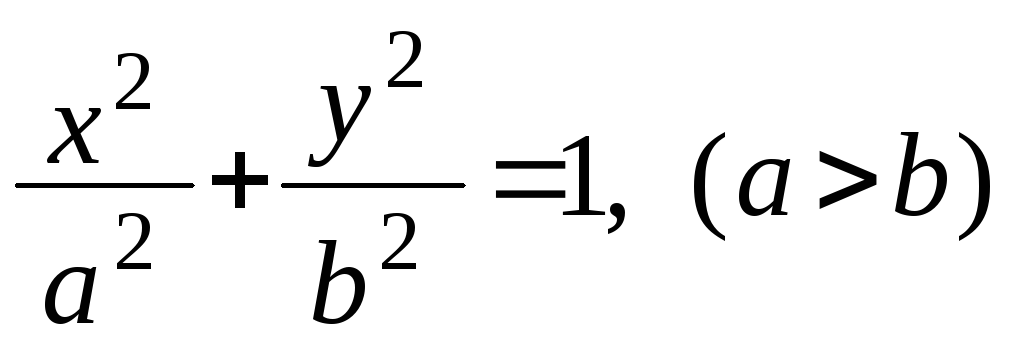 и
двумя прямыми, перпендикулярными к оси
ОХ и проходящими через фокусы эллипса,
вращается вокруг оси ОХ. Найти объем
тела вращения.
и
двумя прямыми, перпендикулярными к оси
ОХ и проходящими через фокусы эллипса,
вращается вокруг оси ОХ. Найти объем
тела вращения.Два тела начали двигаться в один и тот же момент из одной точки в одном направлении. Одно двигалось со скоростью
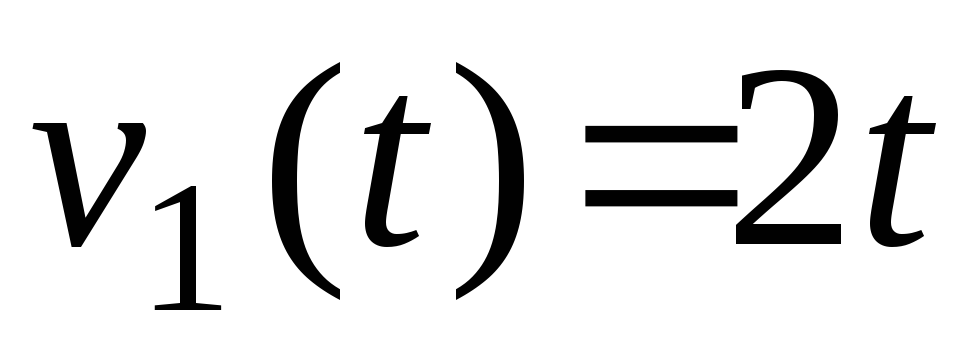 м/с, другое – со скоростью
м/с, другое – со скоростью
 м/с. Какое расстояние между ними было
через 4 секунды?
м/с. Какое расстояние между ними было
через 4 секунды?Вычислить силу давления воды на треугольник с высотой h и основанием а, если он погружен в воду так, что его основание лежит на поверхности воды.
Найдите работу против сил выталкивания при погружении шара радиуса R в воду.
Дополнительные задачи
Вычислить интеграл
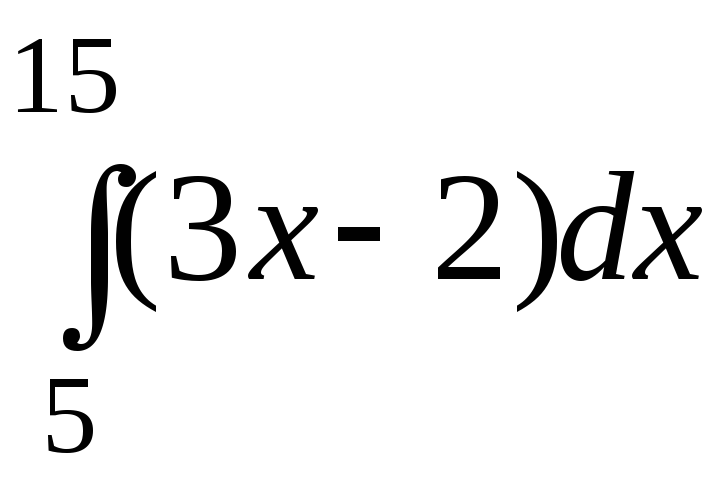 ,
рассматривая его как предел интегральной
суммы.
,
рассматривая его как предел интегральной
суммы.Оценить интеграл
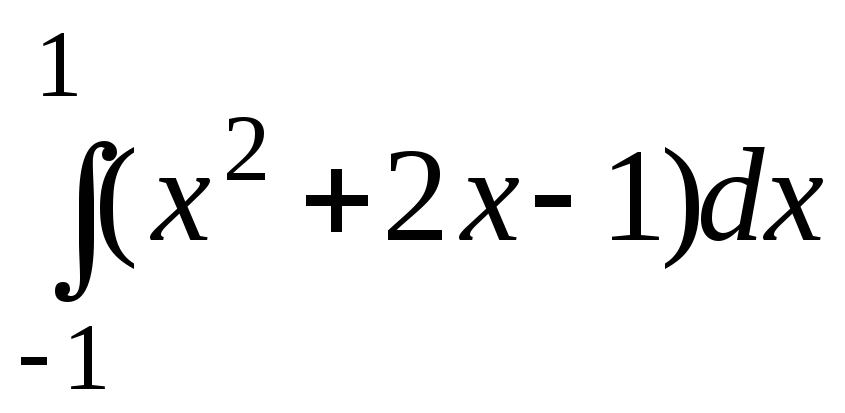 .
.Исходя из геометрического смысла определенного интеграла, найти: а)
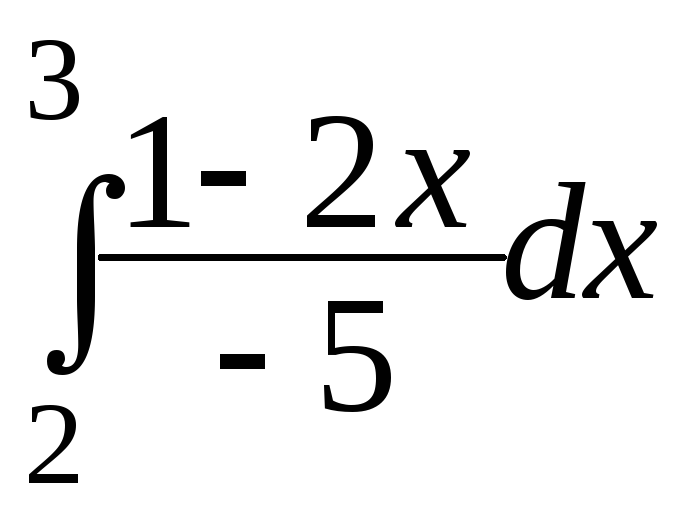 ;
б)
;
б)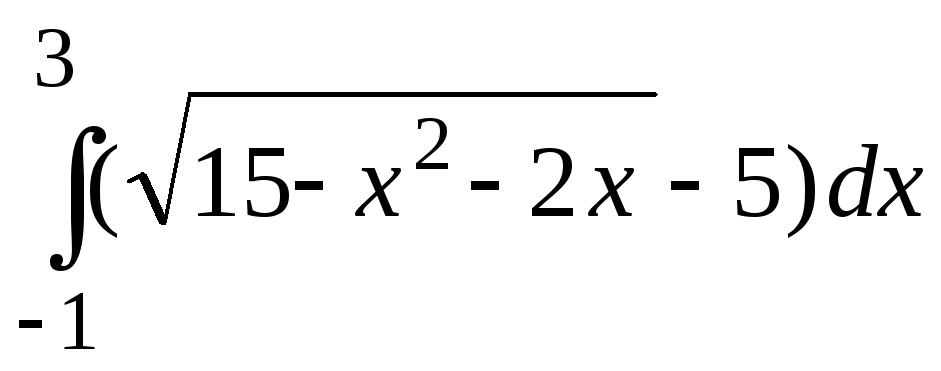 .
.Исследовать сходимость интеграла
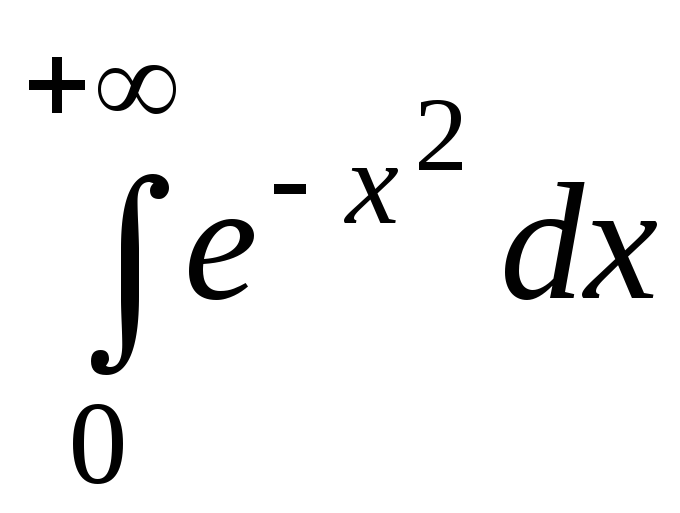 .
.Вычислить
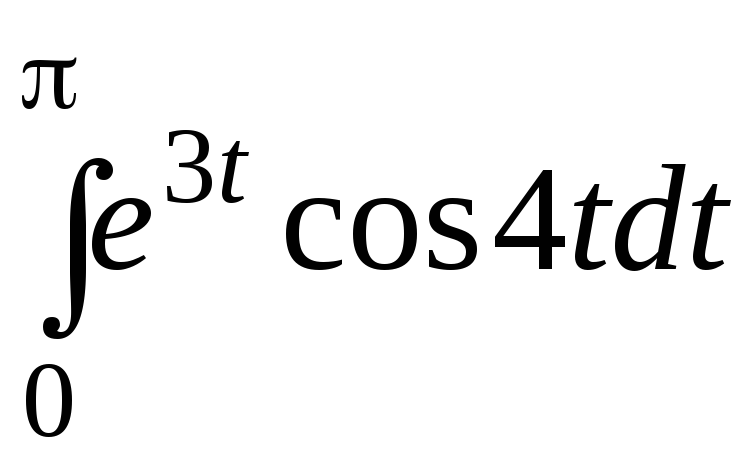 .
.Найти площадь, ограниченную кривой
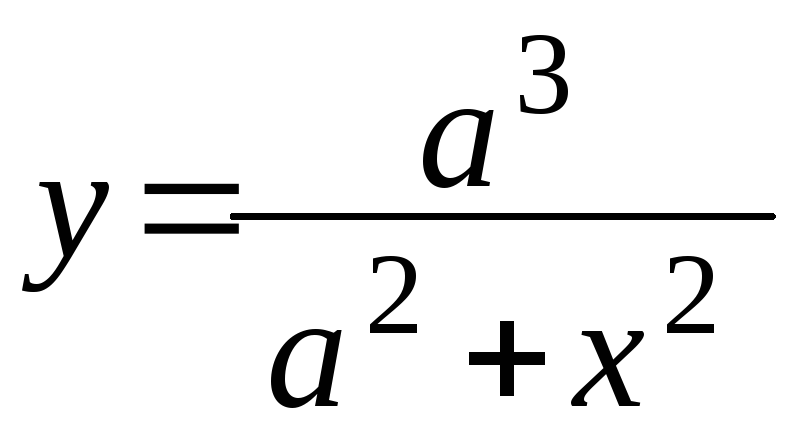 и осью ОХ.
и осью ОХ.Найти длину дуги кривой
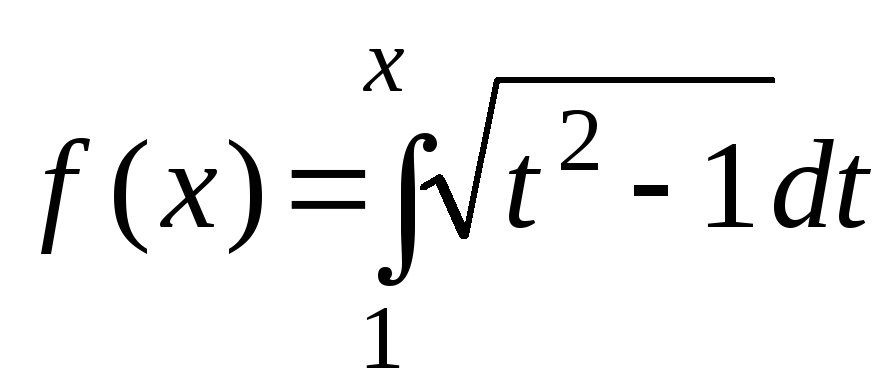 между точками х=0
и х
= 3.
между точками х=0
и х
= 3./4б/ Найти объем тела, полученного от вращения криволинейной трапеции, ограниченной линией
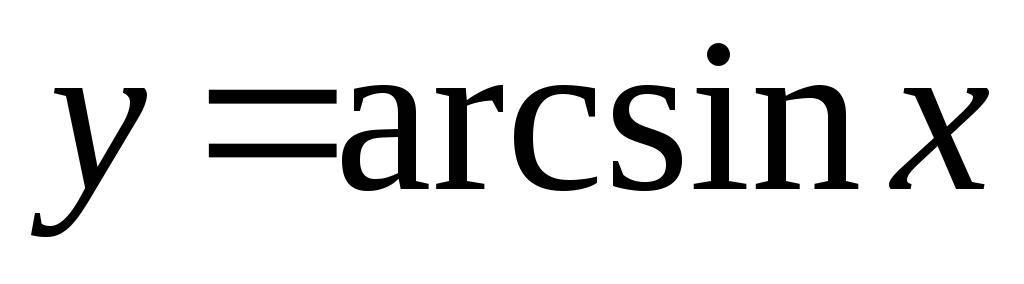 с основанием [0;1] вокруг оси ОХ.
с основанием [0;1] вокруг оси ОХ. /4б/В динамомашине электродвижущая сила переменного тока выражается формулой
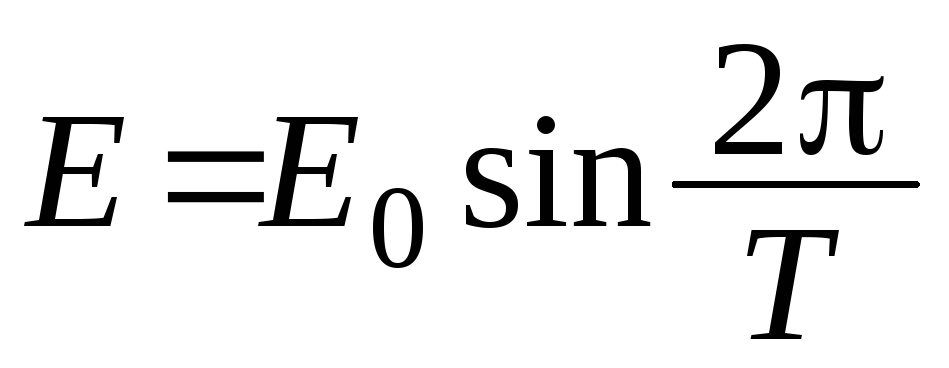 ,
где Т
– продолжительность периода в секундах;
Е0
- амплитуда.
Найти среднее значение электродвижущей
силы на отрезке
,
где Т
– продолжительность периода в секундах;
Е0
- амплитуда.
Найти среднее значение электродвижущей
силы на отрезке
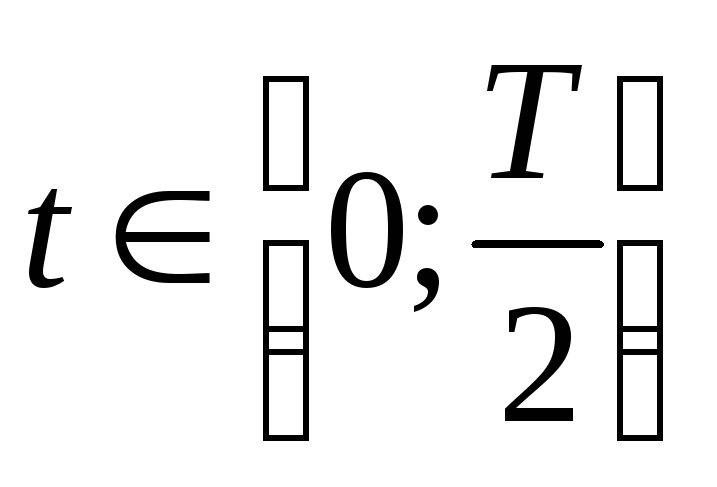
ОТВЕТЫ. Часть 1. 1. а) да; б) нет; в) нет.
2.0. 3. а)
![]() <
<![]() ;
б)
;
б)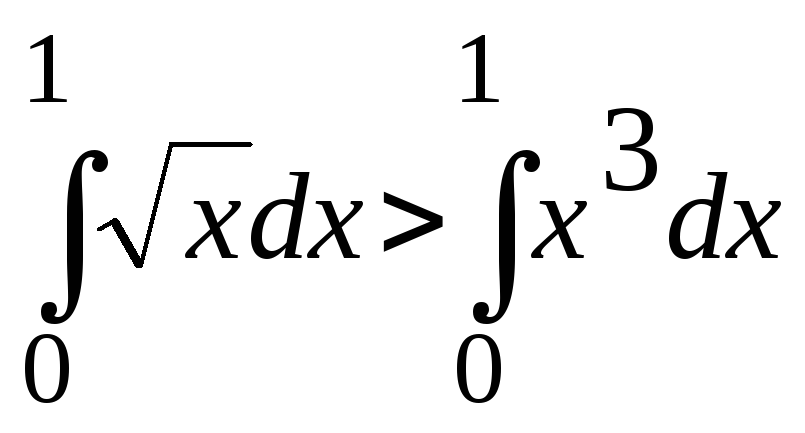 .
.
4.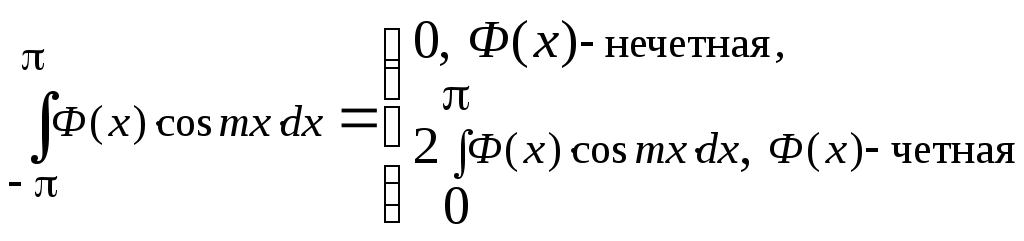 ,
,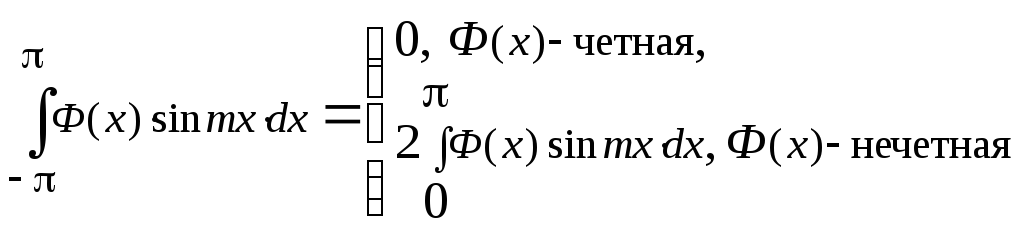 .
.
5. а) 2/5 б)![]() в)arctg4–arctg3
г)
в)arctg4–arctg3
г)![]() д) π/6 е)
д) π/6 е)![]() ж) 0 з) ω(е–2) 6. 0,5(е2–
1) +sin1 7. а) расходится
б) 0,5е–1. Часть 2. 1.
а) 4 б) πа2/2 2. а) 0,5(еа
– е–а) б)6R3.
ж) 0 з) ω(е–2) 6. 0,5(е2–
1) +sin1 7. а) расходится
б) 0,5е–1. Часть 2. 1.
а) 4 б) πа2/2 2. а) 0,5(еа
– е–а) б)6R3.![]() 4. 80 м 5.аh2/6
6.
4. 80 м 5.аh2/6
6.![]() Указание: объем шарового сегмента высотыhравен
Указание: объем шарового сегмента высотыhравен![]() ,
Архимедова сила выталкиванияF=ρgV
,
Архимедова сила выталкиванияF=ρgV
