2. Свойства определенного интеграла

1. Постоянный множитель можно выносить за знак интеграла

.

2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых):

.

3. При перемене порядка интегрирования знак определенного интеграла меняется на противоположный:

.

4. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b и с справедливо

.

5. Обе части неравенства можно почленно интегрировать, т.е. если для всех , то

.

6. Для определенный интегралстановится функцией от переменного верхнего предела. Производная этой функции равна значению подынтегральной функции в точке:

.

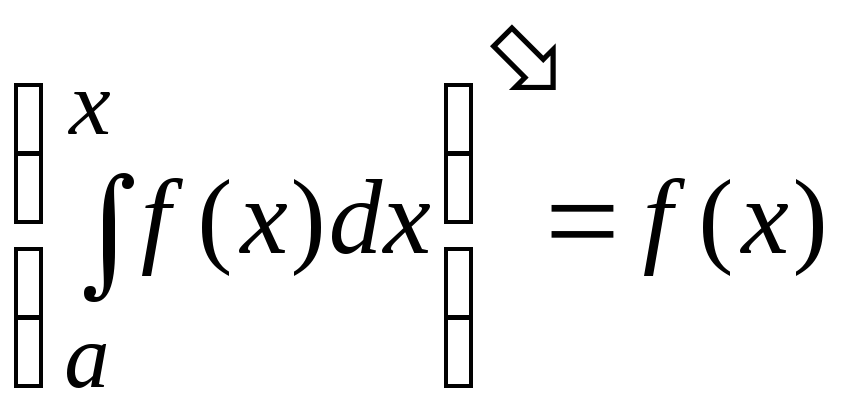7. Теорема о среднем. Если функция непрерывна на, то существует точкатакая, что

.

Значение называетсясредним значением функции на.

у

В

А

Площадь криволинейной трапеции равна площади прямоугольника с основаниеми высотой, равной значению функциив точке .

Геометрически теорема о среднем означает, что на отрезке найдется такая точка, что площадь под кривой на этом отрезке будет равна площади прямоугольника со сторонами и .

3. Формула Ньютона-Лейбница

Формула Ньютона-Лейбница связывает неопределенный и определенный интегралы.

Если функция непрерывна на, а функция- одна из ее первообразных, т.е., тоопределенный интеграл от функции f(х) на [а, b] равен приращению первообразной F(х) на этом отрезке, то есть

.

Эта формула сводит нахождение определенного интеграла к нахождению неопределенного интеграла.

Разность называетсяприращением первообразной и обозначается .

Подчеркнем, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную для подынтегральной функции, например, имеющую наиболее простой вид при С = 0 (в дальнейшем не будем записывать константу при нахождении неопределенного интеграла, поскольку будем считать ее равной нулю).

Пример 1. Вычислить определенный интеграл .

Решение. По формуле Ньютона-Лейбница имеем

.

Пример 2. Вычислить интеграл .

Решение.

.

Пример 3. Вычислить интеграл .

Решение.

На основании свойств определенного интеграла и формулы Ньютона-Лейбница получаем

Контрольные вопросы

1. Как из интегральной суммы получить определенный интеграл?

2. Как меняется определенный интеграл при перемене пределов интегрирования?

3. Чему равен определенный интеграл по теореме о среднем?

4. Какой формулой связаны определенный и неопределенный интегралы?

Тема 4. методы вычисления определенного интеграла. площадь плоской фигуры. несобственные интегралы

Содержание

1. Метод замены переменной в определённом интеграле.

2. Метод интегрирования по частям.

3. Вычисление площади плоской фигуры.

4. Несобственные интегралы

1. Метод замены переменной в определенном интеграле

Пусть функция непрерывна на отрезке, а функциянепрерывна на, причем,и для всехвыполняется. Тогда

.

Пример 1. Вычислить интеграл .

Решение.

Обозначим , тогда,. Подставим старые пределы интегрирования в формулу, получим новые пределы интегрирования,. Следовательно,

Пример 2. Вычислить интеграл .

Решение. Представим дифференциал как , тогда

Пример 3. Вычислить интеграл .

Решение

2. Метод интегрирования по частям

Пусть функции иимеют непрерывные производные на отрезке. Тогда

.

Формула интегрирования по частям в определенном интеграле.

Пример 4.

3. Вычисление площади плоской фигуры

Применение определенных интегралов к вычислению площадей плоских фигур основано на геометрическом смысле определенного интеграла какплощади криволинейной трапеции, ограниченной отрезком , прямыми,и кривой.

Другими словами, в декартовой системе координат за основную фигуру, площадь которой выражается одним интегралом, принимается криволинейная трапеция.