2. Метод подведения функции под знак дифференциала

В данном пункте будем использовать следующее свойство неопределенного интеграла: «неопределенный интеграл не зависит от обозначения переменной интегрирования». Переменной интегрирования может быть не только независимая переменная , но и любая дифференцируемая функция.

Тогда в «Таблице основных интегралов» может быть использовано обозначение , например,, где - дифференцируемая функция.

Как известно, дифференциал функции равен произведению производной функции на дифференциал переменной: .

Метод подведения функции под знак дифференциалав неопределенном интегралеоснован на следующих свойствах дифференциала функции:

1. - под знаком дифференциала можно прибавлять любую постоянную;

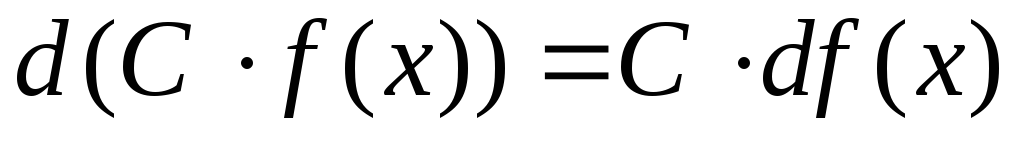2. - постоянный множитель можно выносить за знак дифференциала.

Кроме того, используются известные соотношения:

3. , ;

1. , ;

4. ,

5. ,

6. и т.д.

Пример 2.

1.

2.

3. Метод интегрирования по частям

Пусть , - дифференцируемые функции на промежутке Х. Тогда

, .

Поэтому , или

.

Метод интегрирования по частямзаключается в применении этой формулы. При этом интеграл в правой части формулы должен быть проще, чем исходный.

Пример 3.

1.

=

2.

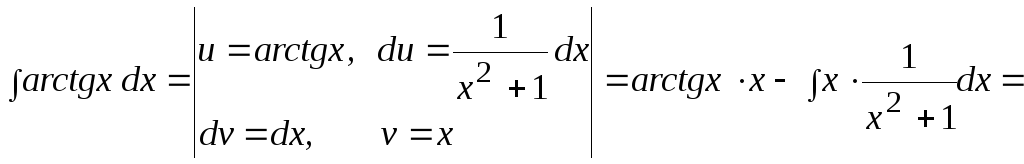
4. Рациональные функции

• Целой рациональной функцией называется многочлен -й степени от переменной, т.е., гдеи целое,.

Например,

• многочлен нулевой степени от переменной - это(число),

• многочлен первой степени от переменной имеет вид,

• многочлен второй степени от имеет вид.

• Дробно-рациональной функцией (рациональной дробью) называется отношение двух многочленов, не имеющих общих множителей, т.е.

.

Рациональная дробь называетсяправильной, если степень числителя меньше степени знаменателя, т.е. . Например,.

Простейшими рациональными дробями являются следующие четыре типа дробей:

I) ; II) (, целое);

III) (); IV) ().

Используя алгоритм деления многочленов «углом», всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной дроби. На основе указанного разложения неопределенный интеграл от неправильной рациональной дроби сводится к сумме интегралов: первый из них является интегралом от многочлена, а второй – интегралом от правильной дроби.

Пример 1. .

Делим числитель на знаменатель:

Тогда .

Пусть знаменатель правильной рациональной дроби разлагается на множители вида ,(дискриминант отрицательный). Тогдаправильную рациональную дробь сначала следует разложить на сумму простейших дробей с неопределенными коэффициентами, найти эти коэффициенты и затем проинтегрировать каждое слагаемое.

5. Интегрирование простейших рациональных дробей

5.1. Простейшая рациональная дробь I-го типа интегрируется заменой переменной :

.

Пример 2. .

5.2. Простейшая рациональная дробь II-го типа () интегрируетсязаменой переменной :

.

Пример 3.

.

5.3. Простейшая рациональная дробь III-го типа (дискриминант) интегрируется с помощью замены переменной .

Пример 4. .

• Выделим в знаменателе полный квадрат и сделаем замену переменной ,:

.

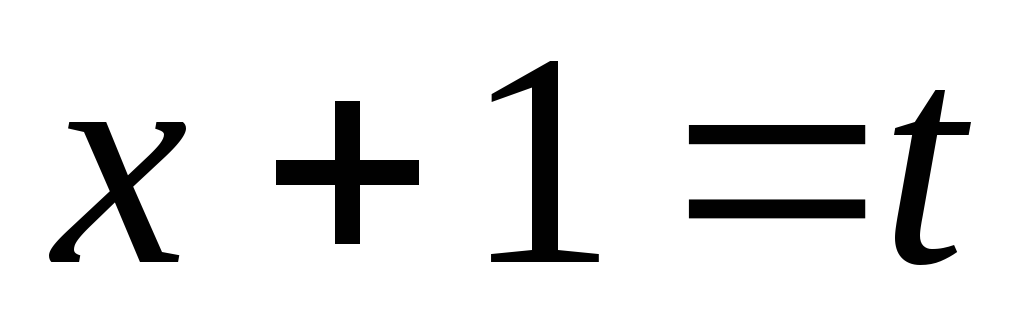• В первом интеграле подведем под знак дифференциала:, а во втором интеграле знаменатель представим как сумму квадратов, тогда

.

• Вернемся к «старой» переменной, выполнив замену , получим

.