24

Модуль 3. Интегральное исчисление функции одной переменной

Содержание

Тема 1. Неопределенный интеграл, его свойства и

вычисление

1. Понятие неопределенного интеграла.

2. Таблица основных интегралов.

3. Свойства неопределенного интеграла.

4. Метод непосредственного интегрирования

Тема 2. Методы нахождения неопределенного интеграла

1. Метод замены переменной интегрирования

2. Метод подведения функции под знак дифференциала

3. *Метод интегрирования по частям

4. Рациональные функции

5. Интегрирование простейших рациональных дробей

6. Интегрирование рациональной дроби ().

Тема 3. Определенный интеграл, его свойства и вычисление

1. Понятие определенного интеграла

2. Свойства определенного интеграла.

3. Формула Ньютона-Лейбница

Тема 4. Методы вычисления определенного интеграла.

Площадь плоской фигуры. Несобственные интегралы

1. Метод замены переменной в определённом интеграле.

2. * Метод интегрирования по частям.

3. Вычисление площади плоской фигуры

4. Несобственные интегралы

Тема 1. неопределенный интеграл, его свойства и вычисление

Содержание

1. Понятие неопределенного интеграла.

2. Таблица основных интегралов.

3. Свойства неопределенного интеграла.

4. Метод непосредственного интегрирования

1. Понятие неопределенного интеграла

В математике есть операции, которые являются обратными. Например, сложение и вычитание, умножение и деление.

Мы изучили операцию дифференцирования, то есть научились по функции находить производную.

Теперь перед нами стоит обратная задача: как, зная производную , восстановить исходную функцию?

Рассмотрим задачу.

Дана функция .

Найти производную , или дифференциал.

Действие нахождения производной или дифференциала называется дифференцированием.

или

Функция Производная (Дифференциал)

Для каждой функции существует единственная производная. Например, для функциипроизводной является, а дифференциалом.

Рассмотрим обратную задачу.

Дана производная или дифференциал.

Найти исходную функцию .

Действие обратное к дифференцированию - нахождение самой функции («исходной, первого образа, прообраза») по ее производной или дифференциалу - называется интегрированием.

или

Первообразная Производная (Дифференциал)

Для производной (или дифференциала) исходной функцией является, а также,и так далее, и вообще, всякая функция вида, где - любая константа.

1. Всякая функция 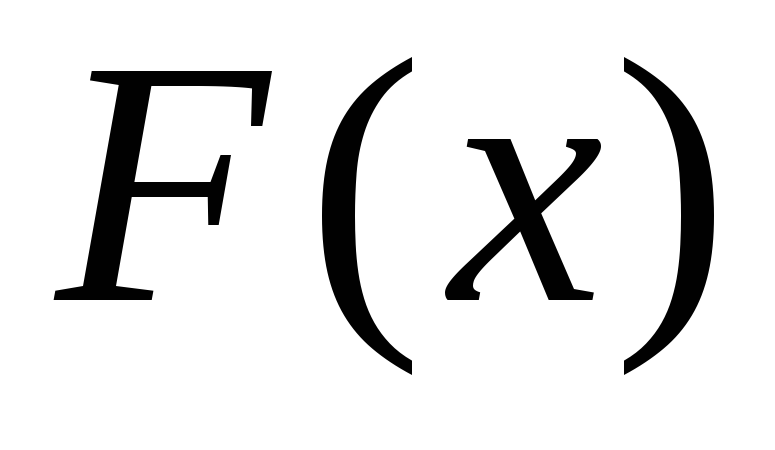, для которой на промежутке Х ее производная равна некоторой функции , называется первообразной функцией для функции , то есть выполняется

.

Для данной функции имеется бесконечное множество первообразных функций, отличающихся друг от друга на постоянную величину.

Графики всех первообразных (интегральные кривые) получаются одна из другой в результате параллельного сдвига кривой вдоль оси ординат.

у

х

Рисунок 1

2. Совокупность всех первообразных 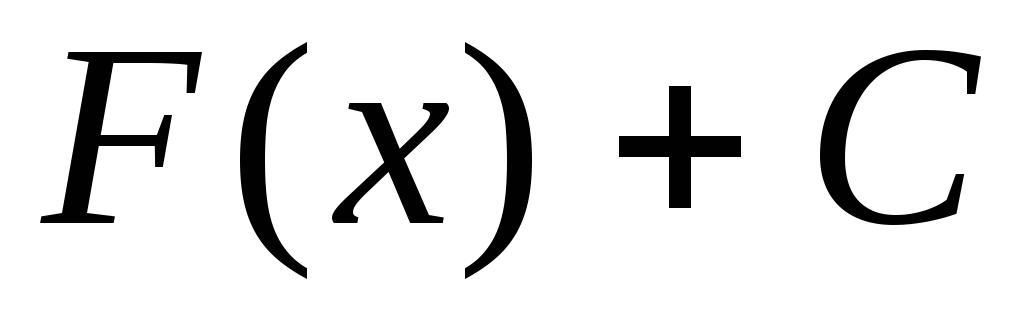для функции 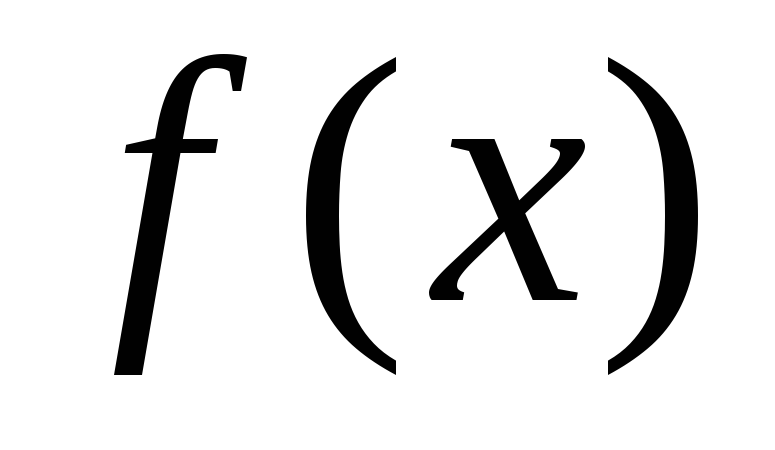называетсянеопределенным интеграломи обозначается .

Если функция является одной из первообразных для функции , то .

Здесь - знак интеграла,- подынтегральная функция,

- подынтегральное выражение, - переменная интегрирования,

- первообразная, т.е. ;

- постоянная интегрирования.

Пример. , где - произвольная постоянная.