Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Национальный исследовательский ядерный университет «мифи»

Волгодонский инженерно-технический институт - филиал НИЯУ МИФИ

Индивидуальные задания

по теме:

«Линейная и векторная алгебра, аналитическая геометрия»

Волгодонск

2010

1. Даны матрицы A, B, C, числа α и β.

Вычислить: а) C^.B; б) α ^.Α + β^.B; в) А²+В²; г) А^-1.

1.1. α =2; β=3;

1.2. 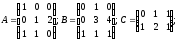α =3; β=3;

1.3. 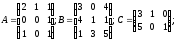α =4; β=2;

1.4. α =2; β=2;

1.5. 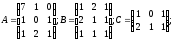α =3; β=5;

1.6. α =4; β=6;

1.7. α =8; β=2;

1.8. 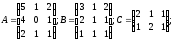α =2; β=3;

1.9. α =3; β=2;

1.10. α =5; β=2;

1.11. α =2; β=3;

1.12. α =5; β=2;

1.13. 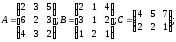α =4; β=6;

1.14. α =3; β=2;

1.15. 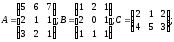α =3; β=2;

1.16. 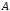=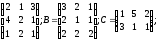α =4; β=3;

1.17. α =3; β=4;

1.18. α =2; β=5;

1.19. 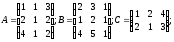α =5; β=5;

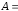
1.20. 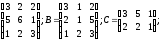α =3; β=2;

1.21. 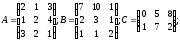α =3; β=4;

1.22. 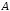=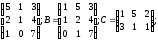α =5; β=4;

1.23. α =2; β=3;

1.24. α =2; β=3;

1.25. α =3; β=2;

1.26. α =3; β=4;

1.27. α =3; β=2;

1.28. α =3; β=4;

1.29. α =5; β=2;

1.30. α =4; β=2.

2. Решить системы линейных уравнений:

а) по формулам Крамера, матричным методом, методом Гаусса;

б) методом Гаусса;

в) методом Гаусса.

2.1. а)	б)	в)
2.2. а)	б)	в)
2.3. а)	б)	в)
2.4. а)	б)	в)
2.5. а)	б)	в)
2.6. а)	б)	в)
2.7. а)	б)	в)
2.8. а)	б)	в)
2.9. а)	б)	в)
2.10. а)	б)	в)
2.11. а)	б)	в)
2.12. а)	б)	в)
2.13. а)	б)	в)
2.14. а)	б)	в)
2.15. а)	б)	в)
2.16. а)	б)	в)
2.17. а)	б)	в)
2.18. а)	б)	в)
2.19. а)	б)	в)
2.20. а)	б)	в)
2.21. а)	б)	в)
2.22. а)	б)	в)
2.23. а)	б)	в)
2.24. а)	б)	в)
2.25. а)	б)	в)
2.26. а)	б)	в)
2.27. а)	б)	в)
2.28. а)	б)	в)
2.29. а)	б)	в)
2.30. а)	б)	в)

3. Даны координаты вершин пирамиды .

Найти: а) угол между векторами ;

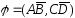б) проекцию вектора на вектор;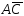

в) площадь треугольника ;

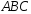г) высоту треугольника 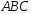, опущенную из вершины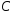

на сторону;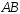

д) обьем пирамиды ;

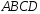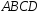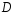е) высоту пирамиды , опущенную из вершинына

основание .

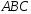3.1.	,	,	,	;
3.2.	,	,	,	;
3.3.	,	,	,	;
3.4.	,	,	,	;
3.5.	,	,	,	;
3.6.	,	,	,	;
3.7.	,	,	,	;
3.8.	,	,	,	;
3.9.	,	,	,	;
3.10.	,	,	,	;
3.11.	,	,	,	;
3.12.	,	,	,	;
3.13.	,	,	,	;
3.14.	,	,	,	;
3.15.	,	,	,	;
3.16.	,	,	,	;
3.17.	,	,	,	;
3.18.	,	,	,	;
3.19.	,	,	,	;
3.20.	,	,	,	;
3.21.	,	,	,	;
3.22.	,	,	,	;
3.23.	,	,	,	;
3.24.	,	,	,	;
3.25.	,	,	,	;
3.26.	,	,	,	;
3.27.	,	,	,	;
3.28.	,	,	,	;
3.29.	,	,	,	;
3.30.	,	,	,	.
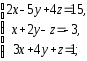
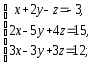
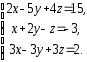
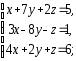
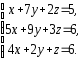
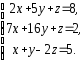
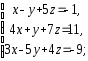
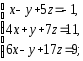
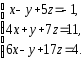
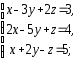
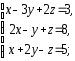
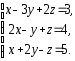
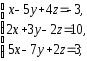
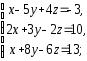
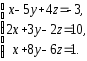
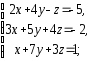
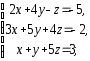
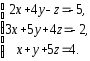
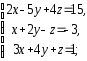
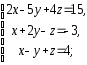
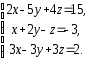
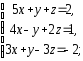
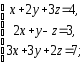
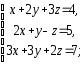
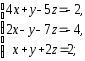
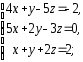
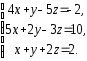
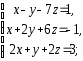
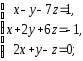
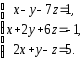
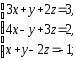
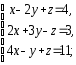
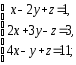
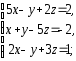
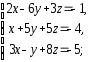
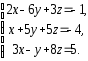
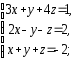
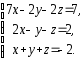
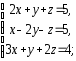
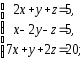
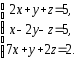
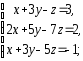
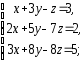
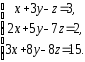
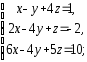
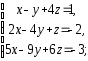
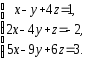
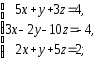
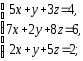
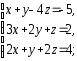
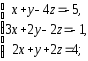
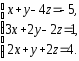
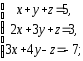
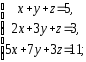
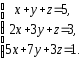
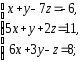
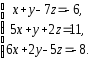
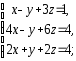
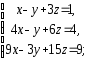
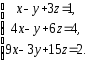
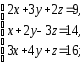
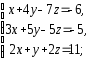
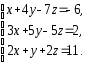
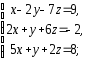
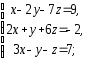
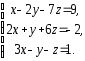
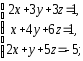
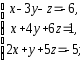
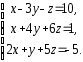
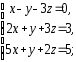
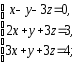
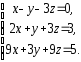
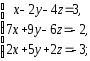
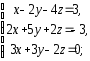
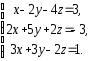
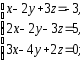
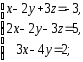
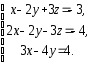
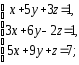
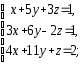
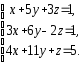
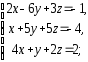
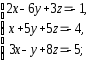
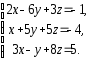
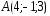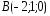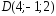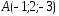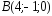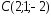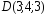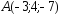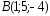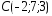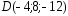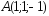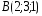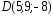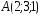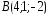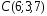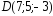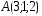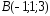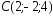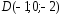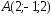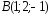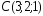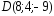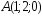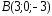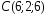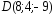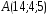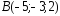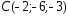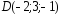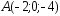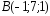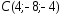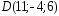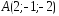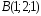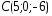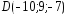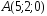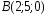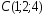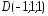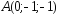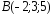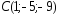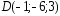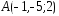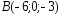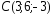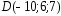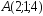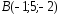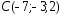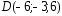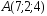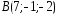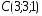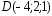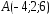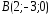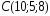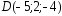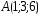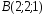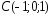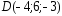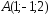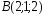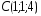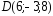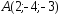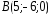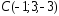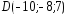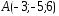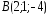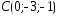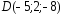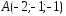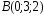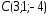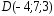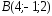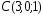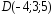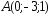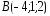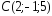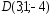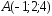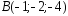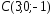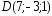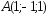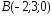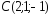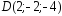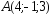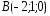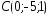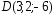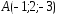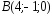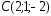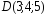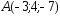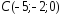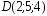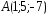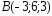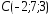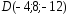