Линейные неоднородные ду 2 порядка с постоянными коэффициентами со специальной правой частью.

Рассм. ДУ

Общее решение такого уравнения:

, где

ФСР - уже рассматривали

Укажем метод нахождения частного решения неоднородного уравнения

, если f(x) имеет специальный вид.

Рассмотрим следующие случаи:

I. ,где - многочлен степени n.

а) - не корень характеристического уравнения

, где - многочлен степениn с неопределенными буквенными коэффициентами. Подставим в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы.

б) - корень характеристического уравнения кратности 1

в) - корень характеристического уравнения кратности 2

2. . ,где M,Nчисла

a) не корень характеристического уравнениянеопределенные коэффициенты.Подставивв ДУ и приравняв коэффициенты при

находим А и В

б) корень характеристического уравнения кратности 1

Замечание : Если в правой части есть толькоили

в частном решении 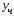должны быть иsin и cos , т.е тригонометрия должна быть полной.

2. .

Где ,-многочлены степенейm и n

a) не корень характеристического уравнениямногочлены степени к с неопределенными коэффициентами

б) корень характеристического уравнения

Метод вариации

Рассмотрим ДУ:

Где правая часть f(x) произвольного вида (необязательно специального).

Общее решение соответствующего однородного уравнения:

, где и- произвольныеconst, - ФСР.

Будем варьировать ии считать, чтоизависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:

(*)

объединим ив систему

- эта система для нахождения иимеет единственное решение, т.к определитель системы,

для системы 2-х ЛНЗ надежнее решать систему по формулам Крамера

, где

, где

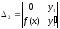
решая систему получим и, проинтегрируем полученные функции по переменной х.

- проинтегрируем по х

, где А и В – константы интегрирования

Таким образом общее решение неоднородного уравнения:

Пример:

1)

Решение систем линейных ду 1 порядка с постоянными коэффициентами способом подстановки

Рассмотрим систему ДУ

, где a,b,c,d – числа.

- искомая функция - функции переменной х

продифференцируем по переменной х первое уравнение системы:

Дифф.(1)

Подставим из (2)

подставим из (1)

перенесем слагаемые с иналево

получим линейное неоднородное ДУ 2 порядка с постоянными коэффициентами. Решая это уравнение получим , продифференцируеми найдём.

Пример:

1)начальные условия: .