Решение

Последовательное соединение двух четырехполюсников (рис. 12.7).Требуется определить параметры результирую­щего четырехполюсника:

Рис. 12.7

Воспользуемся матричным уравнением четырехполюсника в форме параметров.

Уравнение (12.28)для первого и второго четырехполюсника:

Учитывая уравнения:

получим в матричном виде урав­нение последовательно соединенных двух четырехполюсни­ков

(12.32)

Матрица сопротивлений [] результирующего четырехпо­люсника получена в результате сложения матриц сопротив­лений первого и второго четырехполюсника, при условии, что матрицы токов равны

Еще раз напомним: при сложении двух матриц элемент результирующей матрицы, расположенной в i -йстроке иj-м столбце равен сумме элементов, расположенных вi-й строке иj- м столбце первой и второй матриц.

Пример 12.10.Даны матрицы сопротивлений двух четырехполюсников типа

Найти матрицу []результирующего четырехполюсника, составленного из последовательно соединенных двух четырехполюсников

Решение

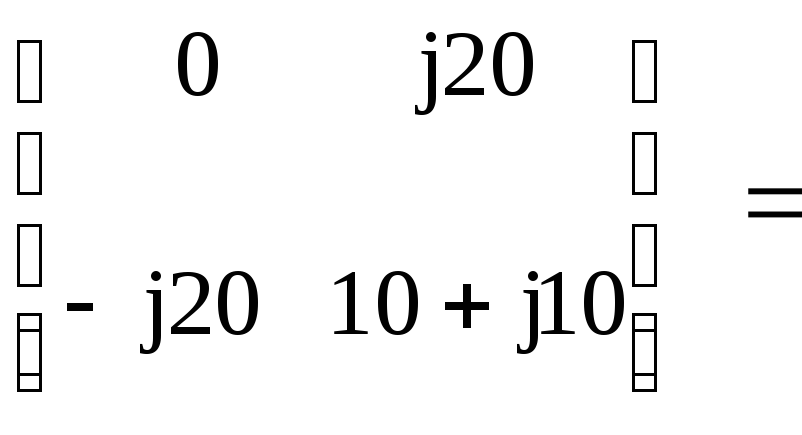
Параллельное соединение двух четырехполюсников (рис. l2.8)

Для определения параметров эквивалентного (относи­тельно зажимов 1-1', 2-2' )четырехполюсника удобно воспользоваться уравнениями сY-параметрами (12.27) ,

Рис. 12.8

так как напряжения и. Заданыпараметры каждого

четырехполюсника [^/ ]и [^// ]. Необходимо найти матрицу [] результирующего

четырехполюсника.

На основании первого закона Кирхгофа для узлов 1и 2 имееми

Тогда в матричном виде

(12.33)

Элементы матрицы проводимостей [ ] результирующего четырехполюсника определяются как суммы соответствующих элементов матриц [^/] и [^//]

Каскадное соединение n-четырехполюсников

Каскадное соединение n-четырехполюсников представляет собой соединение, при котором выходные зажимы (n- 1)-го четырехполюсника соединяются с входными зажимамиn-го четырехполюсника, гдеn-любое целое число большее двух (рис. 12.9).

Рис. 12.9

Соединение такого типа получило наибольшее распрост­ранение на практике (согласование

источника и приемника энергии, линия связи, электрические фильтры и др.), и ис­пользуется в

режиме согласования каждого четырехполюсника и нагрузки. При этом сопротивление нагрузки

рав­но выходному характеристическому сопротивлениюn-го че­тырехполюсника

, а входное характеристическое сопротивлениеn-го четырехполюсника равно

выходному характеристическому сопротивлению (n-1)-го четырехполюс­ника .

Сопротивления ,гдеnпринимает значения 1, 2, 3, ... ,называются

характеристическими сопротивле­ниями n-го звена. Итак, имеем для каждого четырехполюсника

характеристические сопротивления ,,,.......,,и постоянные передачи

g₁, g₂ , g₃ , ......., g_n. В соответствии с уравнением (12.23)имеем

........... ,

(12.34)

Подставляя ток и напряжение последующего звена в предыдущее, получим

Таким образом постоянная передачи эквивалентного четы­рехполюсника равна сумме

постоянных передач каждого четырехполюсника

В случае соединения идентичных симметричных четырехполюсников, каждый

четырехполюсник имеет одинаковое характеристическое сопротивление и постоянную

передачи g при этом входное сопротивление каждого четырехполюсника и всего соединения в

целом равно характеристическому , постоянная передачи

, а. Постоянная передачи результирующего четы­рехполюсника вn- раз

больше постоянной передачи отдельного четырехполюсника. Уравнения каскадно соединенных

и идентичных симметричных четырехполюсников согласно уравнениям (12.25)примут вид

(12.35)

Пример 12.11.Три несимметричных четырехполюсника, соединенных каскадно, имеют

следующие матрицы коэффи­циентов типа А:

Найти характеристические сопротивления и постоянную пе­редачи, входной и выходной токи

результирующего четырех­полюсника при ,.