Вопросы

1. Какие события называются совместными и несовместными, зависимыми и независимыми?

2. Назовите примеры полной группы событий. Какие события называются противоположными? Как вычислить вероятность противоположного события?

3. Как вычислить вероятность появления двух совместных независимых событий: и события А, и событияВ?

4. Как вычислить вероятность появления хотя бы одного из двух совместных независимых событий АилиВ?

3. Законы распределения случайной величины. Де-1.3, 2.10/2.03, 04, 3.04

Одним из важнейших понятий теории вероятности является понятие случайной величины. Случайная величина— это переменная, которая в результате испытания случайным образом принимает одно из своих возможных значений. Случайная величина бывает или дискретной, или непрерывной. Значения дискретнойслучайной величины можно представить в виде отдельных точек на числовой оси.Непрерывнаяслучайная величина принимает возможные значения из конечного или бесконечного интервала.

Случайная величина характеризуется законом распределения. Закон распределенияставит в соответствие значениям случайной величины вероятность их появления.

Закон распределения дискретной случайной величины может быть представлен в виде таблицы:

хi	x1	x2	x3	...	xn
pi	p1	p2	p3	...	pn

где х_i— возможные значения случайной величиныХ;

p_i— соответствующие им вероятности.

При этом должно выполняться следующее равенство:

p₁+p₂+ ... +p_n= 1,

которое называют условием нормировки.

Графическое представление закона распределения называют многоугольником (полигоном) распределения.

Многоугольник распределения лежит в верхней полуплоскости, так как все p_i0.

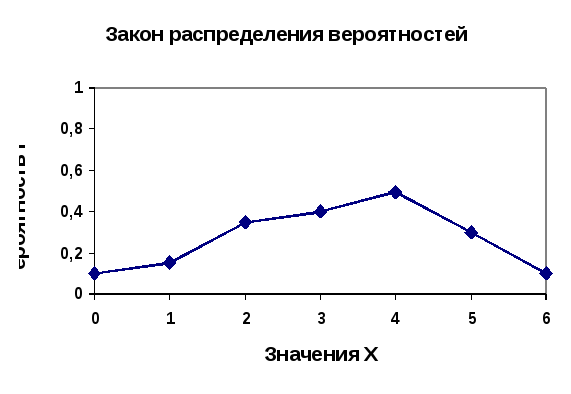
Закон распределения позволяет вычислить основные характеристики случайной величины: математическое ожидание среднего значения (обычно говорят просто «математическое ожидание»):

,

и стандартное отклонение:

.

Пример 1. Найти математическое ожидание и стандартное отклонение для закона распределения, заданного в виде таблицы:

xi	1	4	5	6	
pi	0,2	0,3	0,4	0,1	1,0

Решение. Определим математическое ожидание и стандартное отклонение:

,

.

Пример 2. В результате 10 опытов получены следующие значения случайной величины: 1, 1, 4, 4, 4, 5, 5, 5, 5, 6. Найдите закон распределения в табличной форме.

Решение. В данном случае в законе распределения вместо вероятности будем использовать относительную частоту появления данных значений f_i:

xi	1	4	5	6	
ni	2	3	4	1	10
fi	2/10=0,2	3/10=0,3	4/10=0,4	1/10=0,1	1,0

Закон распределения непрерывной случайной величины задается с помощью функции f(x), которая каждому значениюх случайной величины ставит в соответствие ее вероятностьf(x). Функциюf(x) называютплотностью распределения. При всех допустимыхх функция f(x)0.

Вероятность попадания значений случайной величины х в интервал [a, b] определяется интегрированием:

.

Вероятность попадания непрерывной случайной величины в интервал [a, b] равна площади заштрихованной криволинейной трапеции на графике закона распределения:

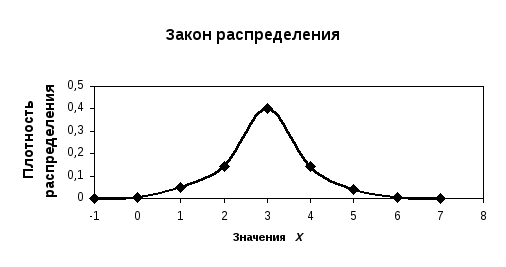
Если непрерывная случайная величина определена на произвольном интервале Δ, то функция плотности распределения f(x) нормируется так, чтобы интеграл по всему интервалу Δ (который численно равен площади криволинейной трапеции, построенной на этом интервале) был равен 1:

^.