Математическая обработка результатов эксперимента / лекция 3
.ppt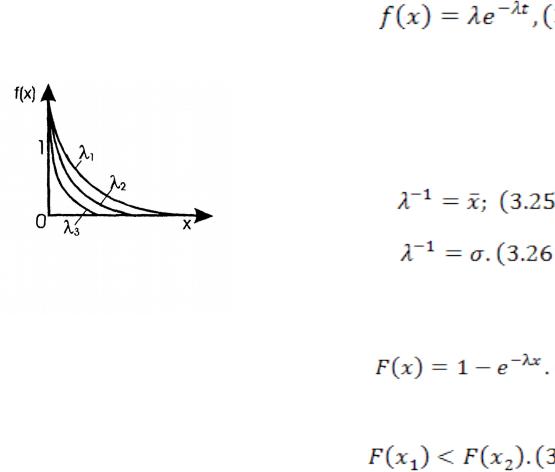
ЛЕКЦИЯ 3. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Моделирование случайной экспоненциально распределенной величины
В теории надежности, а также в других задачах случайная величина, в частности вероятность безотказной работы, подчиняется экспоненциальному закону:
(1)
где λ – интенсивность отказов; t – время.
Рис. 1.. Экспоненциальн
о
распределенны е случайные величины
На рис. 1. приведена плотность вероятности при различных значениях . Для проверки соответствия эмпирического закона распределения экспоненциальному используются его свойства:
(2)
Интегральный экспоненциальный закон распределения случайной величины находится из формулы:
(3)
Интегральная функция является непрерывно возрастающей от нуля до единицы, причем большему значению аргумента соответствует большее значение функции:
(4)
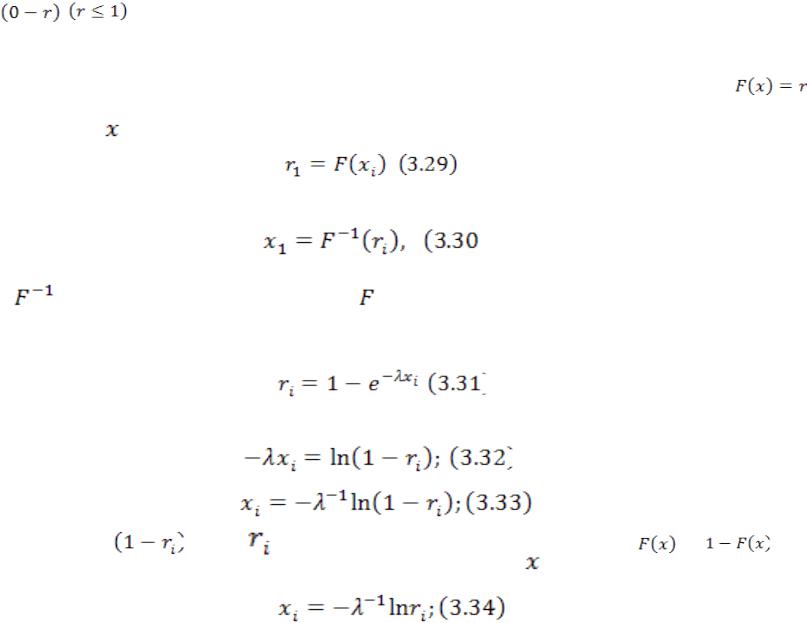
Вероятность попадания случайной величины в интервал
равна длине этого интервала, что является свойством равномерно
распределенной
величины.
Так как интегральная функция в интервале (0 – 1) монотонно возрастает, то уравнение имеет единственный корень. Для получения отдельной реализации непрерывной случайной величины нужно найти значение , при котором
(5)
или
Где |
– функция, обратная по отношению к . |
При заданном параметре экспоненциального закона λ имеем:
(6)
Решив уравнение (3.31) относительно λ, получим:
Случайное число |
, как и |
принадлежит интервалу (0 – 1), т. е. функции |
|
и |
распределены одинаково, поэтому для отыскания случайного числа |
||
можно использовать формулу |
(7) |
||
|
|
|
|
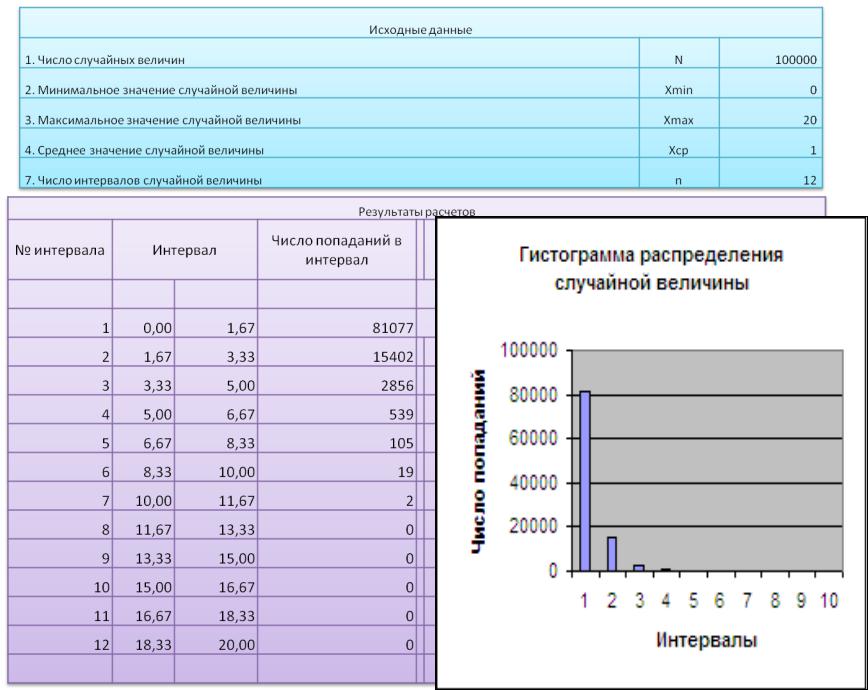
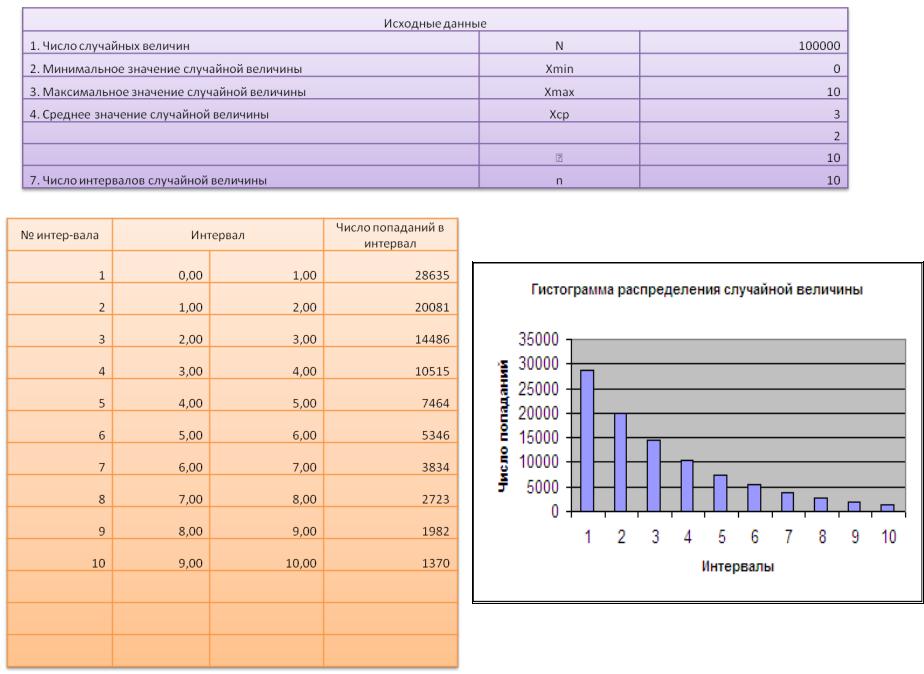
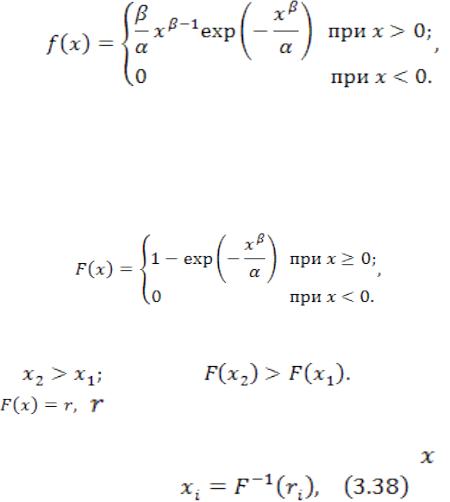
5. Моделирование случайной величины, распределенной по закону Вейбулла
В некоторых практических задачах встречаются случайные величины, распределение которых подчиняется закону Вейбулла. Плотность вероятности имеет
вид: |
(8) |
|
Подбором параметров β и α можно получить хорошее приближение практически к любому эмпирическому распределению.
нтегральная функция распределения Вейбулла выражается формулой:
(9)
Интегральная функция при постоянных параметрах α и β является непрерывно возрастающей от нуля до единицы, т. е. выполняются неравенства:
|
(10) |
Поэтому уравнение |
где – величина, равномерно распределенная в |
интервале (0 – 1), имеет единственный корень. Следовательно, для получения отдельной реализации непрерывной равномерно распределенной величины необходимо отыскать значение , при котором (11)
где |
– функция, обратная по отношению к . Решая уравнение (12), получим |
(12)
Из уравнения (13) находится отдельная реализация случайной величины, распределенной по Вейбуллу:
(13)
Случайное число |
или , |
принадлежит интервалу (0 – 1), т. е. функции |
ираспределены одинаково равномерно. Следовательно, для отыскания
случайного числа |
можно использовать формулу: |
(14)
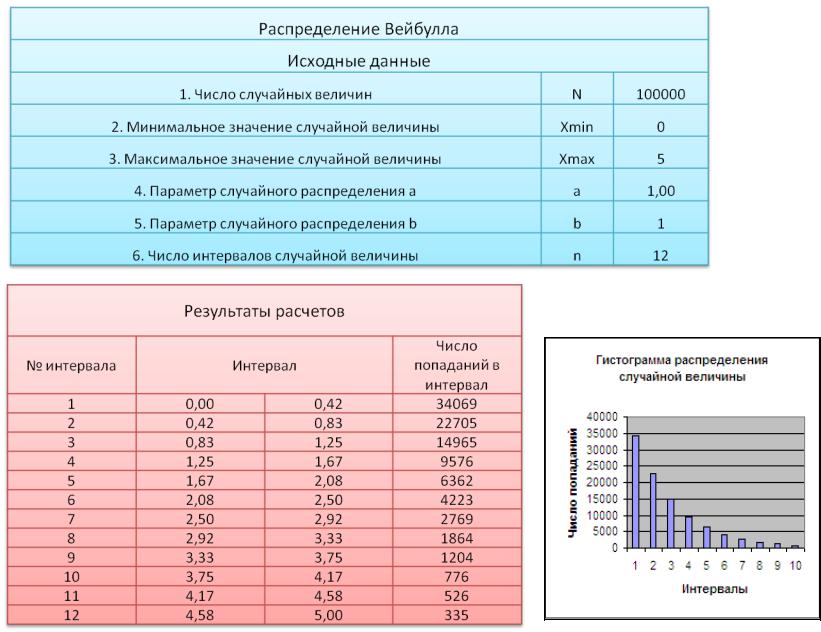
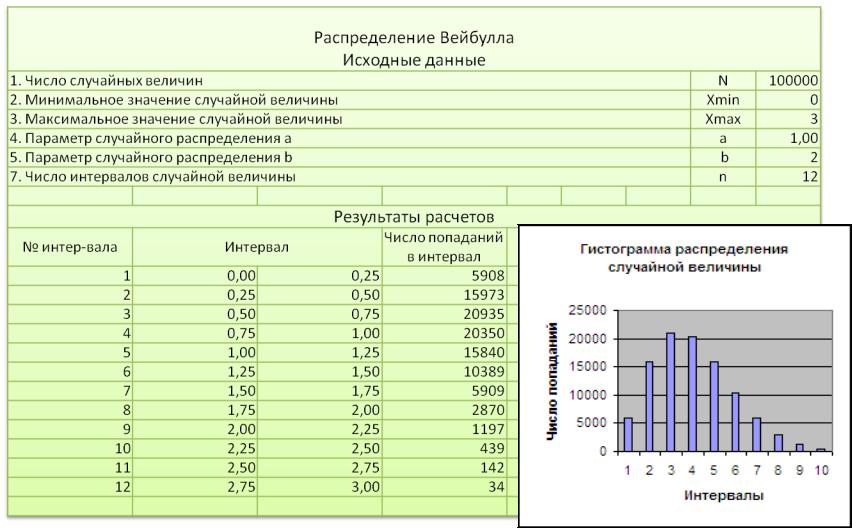
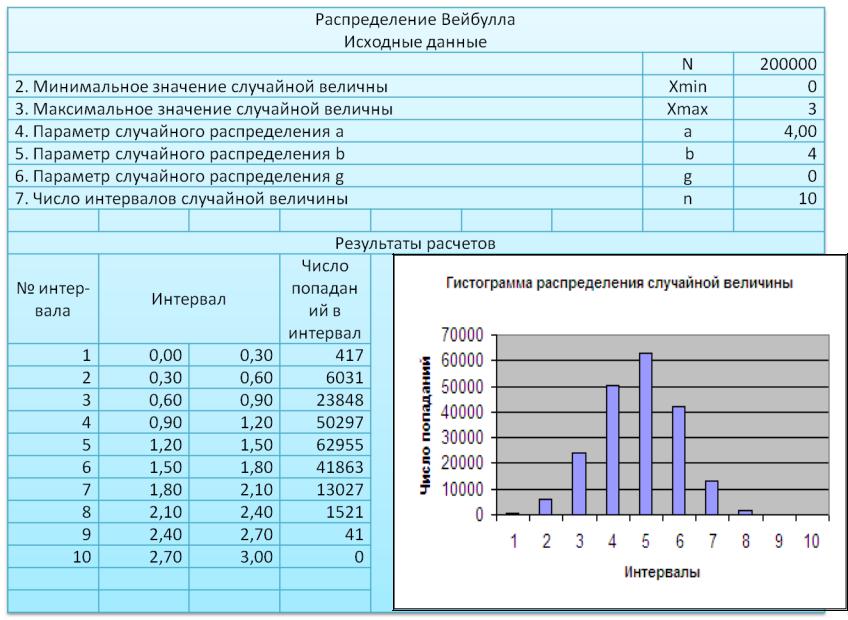
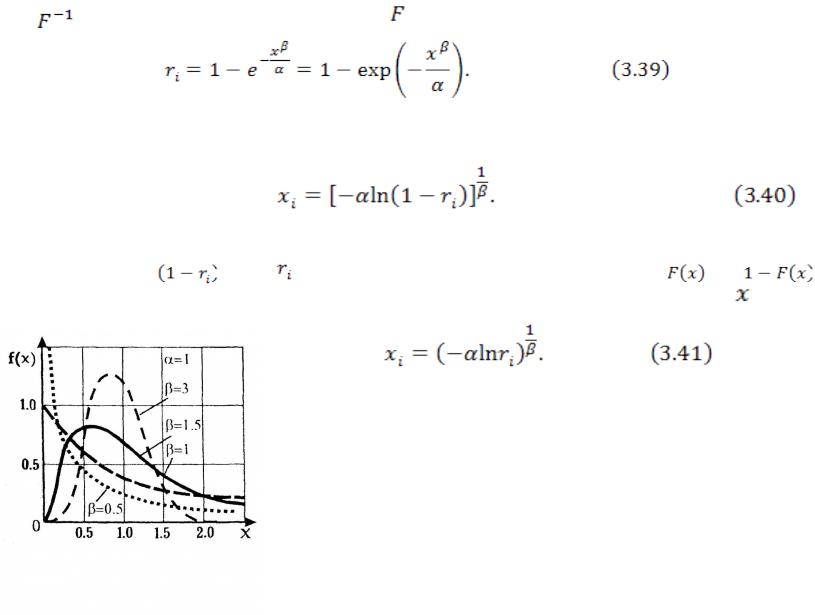
Рис. 2. Распределение Вейбулла
Программа для моделирования случайной величины, распределенной по Вейбуллу, практически аналогична программе для моделирования экспоненциально распределенной величины (рис. 2).
После получения массива случайных чисел производится их статистическая обработка, и по критерию Пирсона определяется соответствие полученного распределения теоретическому, т. е. распределению Вейбулла.