
ЛЕКЦИЯ 4. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Моделирование случайной величины, распределенной по закону Рэлея
Распределение Рэлея встречается в некоторых задачах динамики машин. Плотность вероятности этого распределения имеет вид:
(1)
Интегральная функция распределения Рэлея имеет вид:
(2)
Математическое ожидание и дисперсия этого распределения соответственно:
Интегральная функция при постоянном параметре распределения является непрерывно возрастающей от нуля до единицы. Следовательно, в интервале
выполняются неравенства: |
(3) |
|
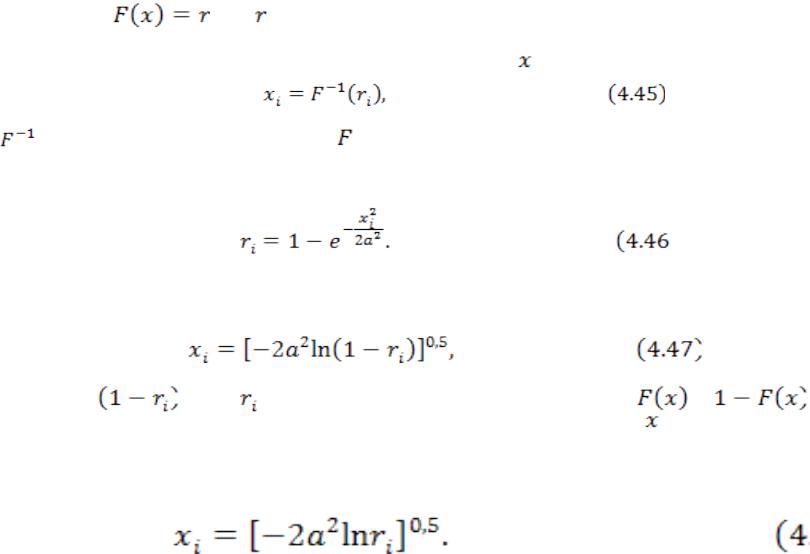
Поэтому уравнение , где – величина, равномерно распределенная в интервале (0 – 1), имеет единственный корень. Следовательно, для получения отдельной реализации непрерывной равномерно распределенной
величины необходимо отыскать значение |
, при котором |
(4) |
|
Где |
– функция, обратная по отношению к . |
|
|
Решая уравнение (5), получим: |
|
|
|
|
|
|
(5) |
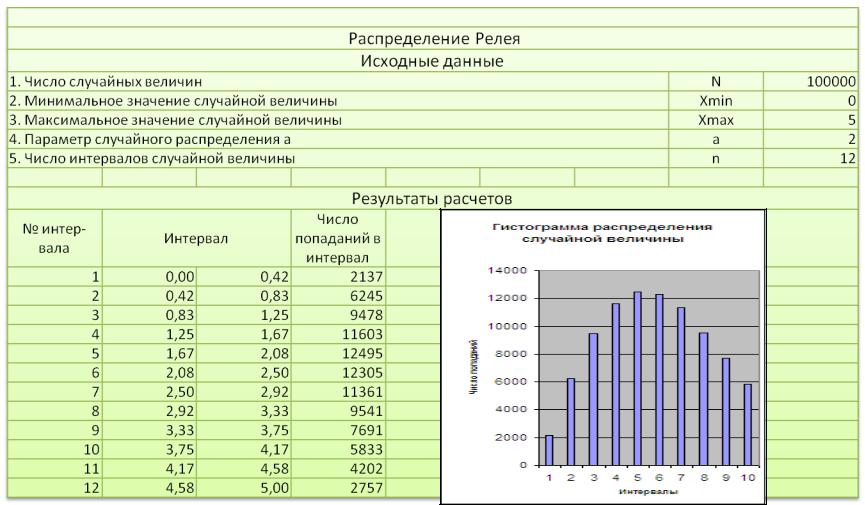
Из уравнения (6) определяется отдельная реализация случайной величины, распределенной по закону Релея:
|
|
|
(6) |
т. к. случайное число |
, как и |
принадлежит интервалу (0 – 1), т. е. |
|
функции |
и распределены одинаково равномерно. Следовательно, для |
||
отыскания случайного числа |
можно использовать формулу |
||
(7)


2. Статистическая проверка соответствия эмпирического распределения теоретическому
Соответствие полученного на ПВЭМ распределения теоретическому производится по критерию Пирсона производится следующим образом:
1.Определяются значения интегральной функции на границе интервала .
2.Для данного интервала находится число случайных чисел:
(8)
где |
– суммарное количество смоделированных случайных чисел; |
–значение интегральной функции формулы (3), при
3.Определяется расчетная величина критерия Пирсона по формуле
|
|
|
(9) |
|
где |
– фактические частоты (количество случайных чисел в |
|
||
соответствующем интервале). |
|
|
|
|
4. Находится число степеней свободы: |
|
(9) |
|
|
|
|
|
|
|
где |
— число интервалов распределения |
|
. |
|
5. По табл. 1 для заданного уровня надежности |
. Если |
находится |
||
критическое значение критерия Пирсона |
, |
то |
||
полученное распределение случайных величин соответствует выбранному закону распределения
Таблица
1
Распределение Пирсона ( )

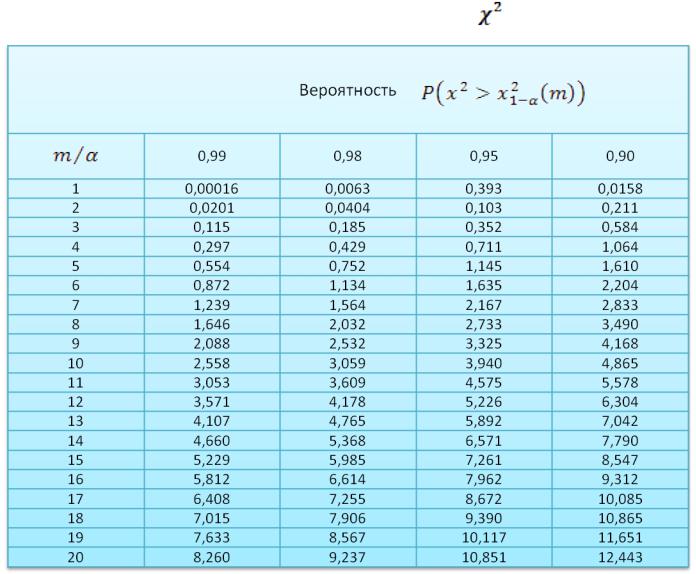
Пример. Определить степень соответствия полученного распределения случайной
величины закону Рэлея (табл. 2, столбцы 1-4) при
.
Таблица 2
Результаты моделирования случайной величины
Табличное значение критерия Пирсона для числа степеней |
свободы |
|
и |
Так как |
, то |
вероятности |
||
можно сделать вывод, что смоделированная статическая совокупность случайных чисел близка к закону распределения Рэлея.
