ЛЕКЦИЯ 19
НЕЛИНЕЙНАЯ РЕГРЕССИЯ ВИДА Y= a0 + a1Х + a2 X2.ПАРНАЯ РЕГРЕССИЯ 1.Нелинейная регрессия
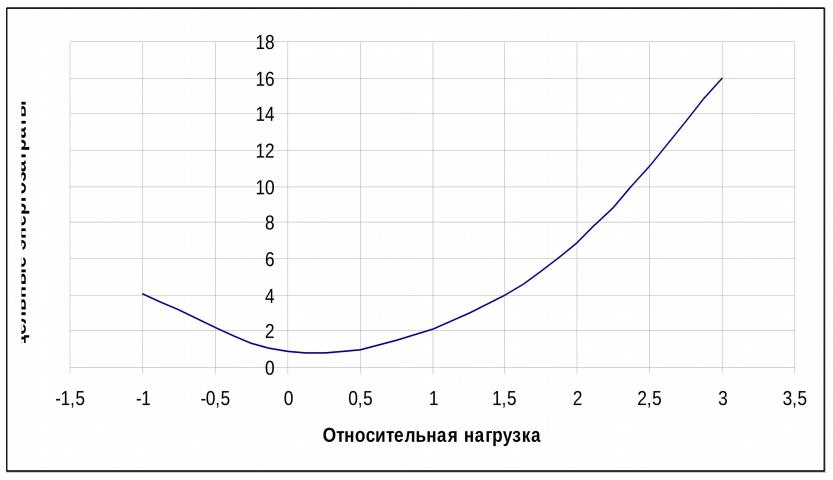
Некоторые процессы в горном производстве описываются нелинейными уравнениями. Например- зависимость удельной энергии необходимой для вибротранспортирования от относительной нагрузки рабочего органа вибропитателя. Для определения коэффициентов регрессии это уравнение необходимо линеаризовать.
Пример: Определить коэффициенты регрессии зависимости удельной энергии необходимой для вибротранспортирования от относительной нагрузки рабочего органа вибропитателя по экспериментальным данным, приведенным в таблице 1. В таблице обозначено : Х – относительная нагрузка рабочего органа; Yi - удельные энергозатраты. В
каждой точке эксперимента проводилось по 3 опыта. На рисунке приведен график зависимости удельной энергии необходимой для вибротранспортирования от относительной нагрузки рабочего органа вибропитателя, построенный по средним значениям в каждой точке эксперимента
Таблица 1.
№ |
Х |
Результаты эксперимента |
Y3 |
|
Y1 |
Y2 |
|||
1 |
-1 |
4,6 |
4 |
3,7 |
2 |
0 |
1 |
1,2 |
0,5 |
3 |
1 |
2,1 |
1,5 |
2,7 |
4 |
2 |
6,5 |
7 |
7,2 |
5 |
3 |
15 |
14 |
19 |
Экспериментальные данные и график показывают, что это уравнение нелинейное и имеет вид:
Y= a0 + a1Х + a2 X2 .
Все расчеты производим в табличной форме (табл.2).
Таблица 2.
|
|
Результаты эксперимента и расчет коэффициентов регрессии |
|
|
|
|||||||||||||||||
№ Х |
|
Y |
1 |
Y |
2 |
Y |
3 |
Y |
cр |
Y |
cр |
Х |
Х 2 |
Х 2 Y |
cр |
Х 3 |
Х 4 |
Y |
расч |
D |
Y |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
||||||||
1 |
-1 |
4,6 |
|
4 |
3,7 |
4,1 |
|
-4,1 |
1 |
4,1 |
|
-1 |
1 |
4 |
|
0,21 |
0,03 |
|||||
2 |
0 |
|
1 |
1,2 |
0,5 |
0,9 |
|
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|
0,13 |
0,03 |
||||
3 |
1 |
2,1 |
1,5 |
2,7 |
2,1 |
|
2,1 |
1 |
2,1 |
|
1 |
1 |
2 |
|
0,36 |
0,03 |
||||||
4 |
2 |
6,5 |
|
7 |
7,2 |
6,9 |
|
13,8 |
4 |
27,6 |
|
8 |
16 |
7 |
|
0,13 |
0,03 |
|||||
5 |
3 |
15 |
16 |
|
17 |
16 |
|
48 |
9 |
144 |
|
27 |
81 |
16 |
1,0 |
0 |
||||||
∑ |
|
|
|
|
|
|
|
30 |
|
59,8 |
15 |
177,8 |
35 |
99 |
|
|
1,83 |
0,12 |
||||
Система уравнений для определения неизвестных коэффициентов имеет вид:
30 = 5 a0 + 5a1 +15 a2 59,8 = 5 a0 +1 5a1 +35 a2
177,8 = 15 a0 +35a1 +99 a2
В результате решения этой системы уравнений получаем: a0 = -1 a1 = 1 a2 =2. Уравнение регрессии имеет вид:
Y= -1 + Х + 2 X2
2. Парная корреляция
Корреляционный анализ позволяет оценивать тесноту связи различных параметров или факторов, влияющих на процесс. В отличие от парной регрессии, определяющей взаимосвязь аргумента, изменяющегося произвольным образом (в том числе и неслучайным), и функции от данного аргумента, парная корреляция вычисляется для оценки взаимосвязи двух случайных величин. Коэффициент парной корреляции является параметром совместного нормального распределения двух случайных величин. Он связан с угловым коэффициентом парной регрессии, но эта связь имеет неформальный смысл только в случае, если функция и аргумент совместно распределены по нормальному закону.
О наличии или отсутствии связи между двумя случайными величинами в первом приближении судят до корреляционному полю. Для численной характеристики тесноты связи между х и у пользуются безразмерной величиной — коэффициентом корреляции.
1.Коэффициент корреляции изменяется в пределах от -1 до +
Положительная корреляция между случайными величинами характеризует такую вероятностную зависимость между ними, при которой с возрастанием одной из них другая в среднем также будет возрастать. При отрицательной корреляции с возрастанием одной случайной величины другая в среднем убывает. Величина коэффициента корреляции определяет тесноту связи между случайными величинами: чем ближе значение к единице, тем теснее статистическая связь. Близкое нулю значение коэффициента корреляции свидетельствует об отсутствии линейной связи.
• Коэффициент парной корреляции определяется по формуле
которую преобразуют к виду
Не всякое значение коэффициента корреляции является достаточным для статистически обоснованных выводов о наличии корреляционной связи между исследуемыми переменными. Надежность статистических характеристик ослабевает с уменьшением объема выборки, а отклонения от нуля полученной величины выборочного коэффициента корреляции оказываются статистически незначимыми. Связь можно считать достоверной, если
•Средняя квадратическая ошибка коэффициента корреляции определяется по
формуле
Если же число , определяются значения некоторой функции , соответствующие крайним значениям доверительного интервала
Истинное значение коэффициента корреляции находится в пределах
Где thz — гиперболический тангенс величины z , определяемый по таблицам гиперболической функции.
Если граничные значения rn имеют тот же знак, что и r , то можно считать, что корреляционная связь между переменными достоверна.
Коэффициент парной корреляции имеет четкий математический смысл только в случае двумерного нормального распределения параметров, т. е. когда для каждого значения x существует совокупность нормального распределения y, и наоборот, а дисперсия зависимой переменной при изменении значений аргумента остается постоянной.
Коэффициент корреляции является довольно грубой оценкой тесноты связи, имеющей смысл лишь при линейной зависимости между параметрами. Даже при высоком коэффициенте корреляции нельзя сделать достоверных выводов о наличии статистической связи, поскольку одновременное регулирование параметров приводит к их искусственной (ложной) коррелируемости. Точно так же малый коэффициент корреляции не всегда является следствием отсутствия связи между параметрами, а может быть результатом нелинейного характера связи.
Между коэффициентом корреляции и угловым коэффициентом линейного уравнения регрессии имеется связь 
т. е. угловой коэффициент численно равен коэффициенту корреляции, если переменные и измерять в масштабе и . Учитывая, что коэффициент корреляции вычисляют относительно центрированных данных, можно записать:
Это значит, что, вычислив характеристики , , r, sy и sx , можно записать уравнение регрессии.
Знание корреляционного отношения позволяет проверить гипотезу линейности связи. При этом считают, что если попадает внутрь доверительных интервалов для r , то связь линейна. Для предсказания средних значений функции необходимо знать доверительные интервалы для коэффициентов уравнения . Для коэффициента a1
Доверительные интервалы для среднего значения
Индивидуальные значения наблюдений, естественно, будут отличаться от вычисленных по формуле (3.18) гораздо больше.
Доверительные интервалы для индивидуальных наблюдений определяются исходя из некоторой доверительной вероятности, например 95 %, по формуле