
глава1
.pdfАналогичные объекты и процессы описываются одинаковыми по форме уравнениями, содержат различные физические величины и параметры, связанные между собой одинаковыми операторами. Величины, которые в аналогичных уравнениях стоят на одинаковых местах, называют аналогами.
Метод аналогии широко используется в различных отраслях науки и техники.
Приведем примеры аналогичного математического описания различных по физической природе явлений:
касательное напряжение в жидкости (закон Ньютона)
τ = –μ grad v;
перенос электрического заряда (закон Ома) i = –g grad U;
перенос тепла (закон Фурье)
q = –λ grad T;
процесс фильтрации (закон Дарси)
w = –k grad p.
Поскольку степень полноты информации о реальных объектах и процессах может быть различной, задача получения модели видоизменяется. В одних случаях, если известны математические связи между параметрами, – это экспериментальное нахождение численных значений постоянных в уравнениях. Если априорно определены и системы уравнений, описывающие связи между параметрами, и постоянные величины в уравнениях математического описания, цель может состоять в поиске математического метода решения задачи, например, в разработке алгоритма решения и определения условий стыковки субпроцессов.
Итогом этапа исследования математической задачи для теоретически полученных моделей является конечный вид формулы, полученной из исходных уравнений, алгоритм или вычислительная программа расчета модели, готовые к использованию.
Эмпирический (экспериментальный) путь получения моделей используют для объектов с низким уровнем информации. Объект представляется как «черный ящик». О нем обычно имеются сведения лишь о входных и выходных параметрах, но полностью отсутствует система уравнений связи между ними. Информацию для составления модели получают в результате экспериментального изучения внешних проявлений свойств объекта с помощью измерений переменных на внешних входах и выходах. Вид и коэффициенты модели определяют с использованием методов регрессионного, корреляционного, дисперсионного анализов и факторного планирования эксперимента. Исследование математической задачи экспериментально получаемой модели – это, например, расчеты коэффициентов модели, анализ значимости факторов, эффективности взаимодействий, то есть все процедуры, связанные с формированием конечного вида регрессионного уравнения.
Экспериментальный путь получения моделей применяется в различных вариантах. Если экспериментальные данные для модели получены путем планирования и изменения условий опытов, а затем специальным образом обрабо-
11
таны, то это активный путь. Он позволяет предусмотреть все необходимые режимы при эксперименте и рационализировать обработку и использование результатов. Полученные формально, такие модели обычно описывают небольшую часть гиперповерхности вокруг центра плана. Они хорошо подходят для решения задач отыскания лучших режимов работы установок, так как методы оптимизации на простых моделях также не вызывают трудностей. Активный путь экспериментирования получил большое распространение.
По сравнению с аналитическими моделями модели, полученные планированными экспериментами, не позволяют отыскивать глобальный (абсолютный) оптимум, а лишь дают возможность улучшить процесс.
Экспериментальная модель может быть получена пассивным путем, когда сбор данных для модели состоит в пассивном наблюдении за изменением условий опытов и их результатов, что затрудняет последующую обработку и использование результатов. В производственных условиях непрерывных процессов пассивный путь приемлемей, поскольку он не требует специальной организации, вмешательства в процесс. Кроме того, не все факторы могут быть изменены; это, например, содержание металла в руде, влажность руды, температура окружающего воздуха. Можно только наблюдать за изменением свойств реагентов, износом машин и т. п.
По своей сути модели, полученные пассивным путем, не отличаются от моделей, полученных активным путем, разве что имеют меньшую точность при равном числе наблюдений. Преимущества пассивного пути в том, что при его применении не нарушается естественный ход процесса.
Модели, получаемые пассивным путем, тоже описывают лишь некоторую область гиперповерхности и служат в основном для отыскания лучшего, по сравнению с известными, режима работы установки.
Пассивным путем можно получать линейные и нелинейные модели. Общий метод получения – регрессионный анализ. Существует метод получения уравнений с использованием данных по мере поступления без накопления в памяти – адаптационный метод. Он может применяться и в планированном активном подходе.
Эвристический путь отличается формализацией модели процесса, существующей в памяти рабочего или инженера, ведущего процесс, который составил такую модель в результате длительного взаимодействия с объектом, но не формализовал ее, т. е. не записал в виде уравнений.
Характер получения таких моделей по существу представляет мысленный активный либо пассивный эксперимент.
Полученные в конечном виде модели могут быть по-разному представле-
ны.
Аналитические модели представляют собой выражения выходных параметров как функции входных и внутренних параметров, полученные путем решения уравнения (системы уравнений) математического описания объекта. Исходные уравнения могут быть заданы в алгебраическом, дифференциальном, интегральном, матричном виде и др. Аналитическая модель в конечном виде – это формула или набор формул.
12
Алгоритмические модели выражают связь выходных переменных с параметрами внутренними и внешними в виде алгоритмов. Алгоритм – это последовательность преобразований, действий приводящих к численному получению результата при заданных исходных данных. Такие модели используют в случае сложных объектов, в которых можно выделить несколько характерных субпроцессов, описываемых различными системами уравнений, при их решении требуется большой объем вычислительных операций. Задаваемый алгоритмом вычислительный (алгоритмический) процесс начинается с произвольного исходного данного из некоторой совокупности возможных для этого алгоритма исходных данных. Пользуясь алгоритмическими процедурами, получают полностью определяемый результат. Затем по оговоренным правилам исходные данные для расчета изменяются, дальнейшие вычисления дают следующий результат и т. д.
В наиболее сложных случаях, особенно при отсутствии достаточной информации о реальном объекте, при невозможности проведения экспериментов на реальном объекте из-за больших затрат времени или средств либо при отсутствии самого объекта в природе, например, при конструировании принципиально нового аппарата, используют имитационные модели. Применение имитационных моделей целесообразно и в том случае, если не существует законченной математической постановки задачи, либо не разработаны аналитические методы решения сформулированной математической задачи, или при наличии аналитических методов решения математические процедуры слишком сложны и трудоемки, или недостаточна математическая подготовка персонала.
Все имитационные модели в целом представляют собой модели типа «черного ящика», то есть они обеспечивают выдачу выходного сигнала системы, если на ее взаимодействующие системы поступает входной сигнал. Поэтому такую модель нельзя «решить», для получения интересующей информации необходимо осуществить «прогон» имитационной модели.
Имитационные модели служат для анализа поведения системы лишь в условиях, определяемых экспериментатором. С их применением нет необходимости предварительно выводить единое уравнение для сложного объекта. Сочетание аналитического и алгоритмического описания узлов аппарата, фаз процес-
са, их стыковка, дополнение модели |
|
|
|
|
|
|
|
|
|
|
|
|
|
элементами, позволяющими по опре- |
|
|
|
|
|
|
в |
|
|
г |
|||
|
|
|
|
|
|
|
|
||||||
деленным процедурам выбрать значе- |
а |
|
|
б |
|
|
|
||||||
|
|
|
|
|
|||||||||
ния входных и внутренних перемен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных, параметров из отводимой для них |
д |
|
|
е |
ж |
|
|
|
|
|
и |
|
|
|
|
|
з |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
исследователем области варьирования, делает модель имитационной. На такой модели ставятся эксперименты с целью либо объяснить поведение системы (модели), либо оценить различные стратегии, обеспечивающие функционирование данной системы, т. е. осуществить прогноз поведения показателей
13
вразличных ситуациях, оптимизировать поведение системы при разном сочетании факторов, в том числе научиться рационально управлять системой.
Поскольку такие модели создаются чаще при отсутствии полной информации о реальном объекте, они после накопления и анализа данных на каждом последующемэтапе моделирования могут совершенствоваться.
Вконечном виде алгоритмические и имитационные модели представляются
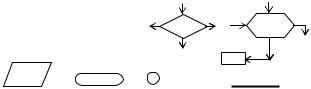
ввиде блок-схем или вычислительных программ, для составления которых могут быть рекомендованы следующие условныеобозначения (рис. 1.4).
1.4.5. Использование принципа декомпозиции
При построении моделей сложных объектов стремятся к упрощениям. Упрощение может осуществляться двумя путями: первый – пренебрежение деталями, что связано с потерей точности, сужением области применения, снижением прогностической мощности модели, второй – это использование идеи декомпозиции сложного объекта, когда упрощение достигается за счет разбиения объекта на части, характерные зоны, операции. В этом случае сохраняются все достоинства сложной модели, но облегчается её составление и использование. Математическое описание поведения системы в разных зонах, операциях может быть различным, поскольку действующие на частицы силы в характерных зонах отличаются друг от друга. Так, для магнитного сепаратора это, по крайней мере, зоны ввода материала, разделения под действием магнитной силы, транспортирования и разгрузки магнитного и немагнитного продуктов.
Если поведение в характерных зонах или операциях математически описано, вводятся начальные и конечные условия для каждой из них, далее отдельные части объединяются в единую модель путем последовательного расчета, например, исходя из логики процесса, либо путём формального приравнивания начальных условий последующего субпроцесса к конечным условиям предыдущего.
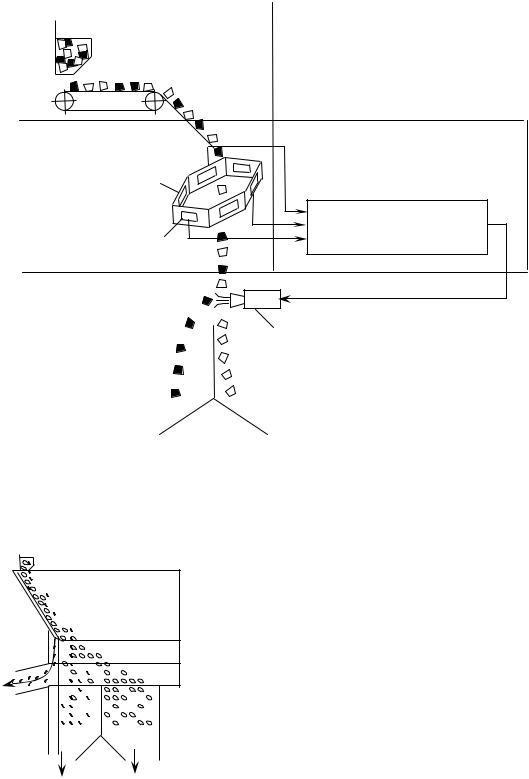
Последовательность операций при фотометрической сепарации иллюстрируется на схеме сепаратора (рис. 1.5). Первая операция – подготовительная, формирование потока, введенная для придания частицам постоянной траектории движения, вторая операция – фотометрический осмотр, третья – принятие решения об удалении частицы, четвертая – удаление частицы из потока.
В данном примере все операции необходимы, взаимосвязаны, но описываются различными уравнениями. Описание поведения частицы в полете и процесса получения и преобразования информации о ней вряд ли возможно одним классом уравнений. Движение частиц описывается дифференциальным уравнением, процесс принятия решения – логическими процедурами.
Высказанное иллюстрируется также примером моделирования при проектировании процесса воздушной сепарации и полочного воздушного сепаратора.
14
|
Формирование |
|
|
|
|
|
потока |
|
|
|
|
Фотометрический |
Принятие решения об удалении |
|
|||
|
|
|
|
||
осмотр |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Вычислительное устройство |
|
||
|
1 |
|
|
|
|
Удаление из потока (распреде- |
|
|
|
|
|
ление по продуктам) |
|
|
|
|
|
|
|
3 |
|
|
|
Продукт 1 |
Продукт 2 |
|
|
|
|
Рис. 1.5. Разделение процесса фотометрической сепарации по операциям: |
|
||||
1 – фотоприемник; 2 – осветитель; 3 – пневматический клапан |
|
|
|||
|
|
Можно выделить три фазы движе- |
|||
|
I |
ния материала в сепараторе (рис. 1.6): |
|||
|
первая – движение материала по наклон- |
||||
|
|
||||
|
|
ной полке, где происходит расслоение |
|||
|
II |
потока перед вводом в камеру аппарата; |
|||
|
вторая – |
распределение сепарируемого |
|||
|
|
||||
Слюда |
III |
материала по граничащим друг с другом |
|||
Воздух |
|
потокам с преобладанием в каждом мо- |
|||
|
|
номинеральных частиц, происходящее в |
|||
|
|
зоне подготовки в момент отрыва частиц |
|||
Промпродукт |
Кварц, |
от нижней кромки наклонной полки до |
|||
ввода в зону воздушной сепарации; третья |
|||||
Рис. 1.6. К объяснению распределе- |
фаза – распределение компонентов под |
||||
ния частиц на полочном воздушном |
действием |
воздушного |
потока, |
направ- |
|
сепараторе: |
|
ленного по нормали к вектору скорости |
|||
I – движение по наклонной полке; |
|||||
II – формирование веера свободно |
сепарируемых частиц. |
|
|
||
падающих частиц; III – распределе- |
Другой простейший пример исполь- |
||||
ние материала по продуктам под воз- |
зования этой руководящей идеи расчета с |
||||
действием воздушного потока |
помощью моделей реальных машин и |
||||
|
|
||||
процессов (декомпозиция объекта – описание частей – стыковка моделей частей |
|||||
15

– анализ) – задача описания работы двух последовательно соединенных камер
(рис. 1.7).
Концентрат Концентрат
|
Камера 1 |
|
Камера 2 |
|
M0 |
|
M1 |
|
M2 |
|
|
|
|
Хвосты |
|
|
|
|
εк = M0 − M 2 = 1− M 2 .
M0 M0
Используем выражения для извлечения в хвосты:
εх1 = |
M1 |
= |
|
1 |
; εх2 = |
M2 = |
1 |
. |
|
1+ kτ |
1+ kτ |
||||||
|
M0 |
|
M1 |
|
||||
Извлечение в хвосты второй камеры:
|
|
|
|
|
|
M |
2 |
|
1 2 |
|
ε |
х |
= ε |
ε |
х2 |
= |
|
= |
|
. |
|
|
|
|||||||||
|
|
х1 |
|
M0 |
1+ kτ |
|||||
|
|
|
|
|
|
|||||
Извлечение в концентрат двух камер:
|
|
1 2 |
kτ(2 + kτ) |
|
|||
εк = 1− εх = 1 |
− |
|
|
|
= |
|
. |
|
|
(1+ kτ)2 |
|||||
|
1 |
+ kτ |
|
|
|||
Решение обратной задачи декомпозиции – стыковки моделей элементов в единую модель, весьма полезно при работе с известными моделями составных частейипозволяетпросторешатьнекоторыетехнологические задачи.
1.4.6. Адекватность и полезность моделей
Поскольку любая модель – лишь некий образ реального объекта, причем характеризующий его не полностью, неизбежно расхождение поведения объекта и его модели. Поэтому после получения до использования модель должна быть проверена на адекватность. Под адекватностью следует понимать точность прогноза по модели по отношению к поведению реальной системы, выраженную в количественных показателях. Например, адекватность математического описания в экспериментально полученных моделях может быть количественно оценена путем, сопоставления экспериментальных и предсказанных по модели результатов, получения значения дисперсий остаточной и воспроизводимости, сравнения их отношения со значениями таблично заданных статистических критериев
16
Фишера при известных величинах степеней свободы f1 и f2 и уровней значимости р. Оценка осуществляется исходя из того, что остаточная дисперсия sост2 не должна значимо отличаться от дисперсии воспроизводимости sвосп2 . Сравнение
по критерию Фишера указывает на адекватность регрессионной модели:
Fр = sост2 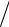 sвосп2 ≤ FТ( p, f1 , f2 ).
sвосп2 ≤ FТ( p, f1 , f2 ).
Во многих случаях количественная оценка адекватности невозможна, а иногда и не требуется. Если моделирование предшествует созданию нового аппарата, то сопоставление поведения объекта и модели по погрешностям прогноза невозможно потому, что экспериментальную информацию просто негде получить. В таких ситуациях допустима проверка модели, в ходе которой достигается приемлемый уровень уверенности исследователя в том, что поведение системы, предсказанное моделированием, будет правильным. Проверка правильности выполняется на качественном уровне и допускает несколько этапов. На первом этапе необходимо убедиться, не дает ли модель абсурдных решений, т. е. объяснимо ли поведение системы с позиции логики её функционирования, гипотез о её возможном поведении. Если решения предсказуемы, модель можно считать адекватной объекту. Непредсказуемость результатов не обязательно указывает на неправильность модели, поскольку для мало изученных объектов допустимо появление неожиданных закономерностей, выявляемых моделированием. Чтобы убедиться в законности непредсказуемого поведения, необходимо сначала проанализировать правильность исходных предложений, допущений и ограничений. Затем в случае их непротиворечивости проверить правильность преобразования информации в самой модели, которая зависит, к примеру, от правильности получения обобщенных формул, преобразования уравнений при стыковке простых описаний субпроцессов в сложных декомпозиционных моделях или определяется качеством составления алгоритмамоделирования и вычислительной программы.
Высокая точность модели требуется отнюдь не во всех моделях. Она нужна, например, при управлении процессами, где неточные сведения могут привести к большим потерям продукции или даже к аварийной ситуации. Требования к необходимой точности модели должен формулировать исследователь. Повышение требований точности не всегда оправдано, поскольку оно идет за счет усложнения модели или удорожания экспериментов, предшествующих получению модели. Можно потратить много времени на улучшение модели, но не достичь заданной точности, например, по причине получения исходных данных для построения модели с большей погрешностью, чем требуемая погрешность модели.
Обычно построение абсолютно адекватной модели не представляется возможным, по крайней мере, стремление к точности временно связано с усложнением уравнении или алгоритмов, с увеличением продолжительности моделирования, с возрастанием затрат на моделирование. По Р. Шеннону, повы-
17
Показатели
Полезность
модели
Стоимость
модели
Выгода/затраты
Точность
Рис. 1.8. К объяснению рациональной точности модели
шение «стоимости» модели за счет стремления к повышению точности увеличивает её ценность для исследователя. Однако рост «стоимости» с увеличением точности прогрессивно возрастает, в то же время «полезность» модели растет не столь значительно (рис. 1.8). Производная от «стоимости» и «полезности» функция выгода/затраты (или прибыль/затраты), по-видимому, имеет экстремум, констатирующий, что дальнейшее повышение точности не целесообразно.
С другой стороны, увеличение сложности модели за счет учета большего количества влияющих на выходные показатели факторов может привести к по-
тере точности или, в крайнем случае, не к повышению ее. В работе |
А. Г. Ивах- |
ненко, посвященной анализу распознающих систем, сказано: |
«... признаки |
могут быть не только полезными, но и вредными. В статистической теории дело ошибочно представляется так, что укорочение входного описания всегда уменьшает информацию и, следовательно, всегда ухудшает распознавание. В действительности, укорочение описания часто приводит к улучшению действия распознающей системы – и это также экспериментально проверенный факт».
Использование излишней информации может оказаться вредным. Покажем, при каких условиях это возможно.
Пусть имеется модель процесса у=(х1, х2 , ..., xi , .... xN).
Вычисление величины у неизбежно связано с ошибками. Понимание причин возникновения ошибок поможет правильно оценивать получаемые результаты и сделать ряд принципиальных выводов по использованию моделей.
На выходной показатель влияет множество (например, N) входных величин х, которые практически учесть невозможно. Если учитывать лишь п величин, то неучет остальных приводит к ошибке в определении величины у, дисперсия которой s21. Для центрированных значений
|
|
N |
|
∂f |
|
2 |
|
2 |
|
∑ |
|
|
2 |
||
s1 |
= |
∂x |
sxi . |
||||
|
|
||||||
|
|
i = n+1 |
|
i |
|
||
Исходная информация может быть получена с некоторой ошибкой εx. Ошибки в определении величины х приводят к появлению ошибки в определении у, дисперсия которой равна s22. Для тех же условий
2 |
n |
∂f |
2 |
2 |
|
|
|
||||
s2 |
|
sε x . |
|||
= ∑ |
|
|
|||
|
i=1 |
∂xi |
i |
||
|
|
|
|
||
Каким бы путем ни была найдена математическая модель, она содержит не точные значения коэффициентов, а отличающиеся от истинных на некоторую величину a. Это приводит к появлению ошибки в определении y, дисперсия которой равна s23. Для центрированных значений
|
n |
|
∂f |
|
|
2 |
|
∂f |
|
2 |
|
∂f |
|
|
n |
2 |
|
2 |
= ∑ |
|
|
|
2 |
|
|
2 |
|
2 |
|
= ∑( |
ai ) |
2 |
|||
s3 |
|
+ |
sxi |
|
sxi |
− 2 |
|
ai sxi |
s x . |
||||||||
|
∂xi |
ai |
− |
|
|
∂xi |
|
||||||||||
|
i=1 |
|
|
|
|
|
∂xi |
|
|
|
i=1 |
|
i |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Принятая модель по какой-либо переменной принципиально не может описать положение экспериментальных точек с бесконечно большой точностью даже при абсолютной точности измерения х. Это объясняется ошибкой аппроксимации по учитываемым переменным s4:
18

n m
s42 = ∑ ∑ s2yij , i=1 j =1
где s2yij – дисперсия, вносимая отсутствующим j-м членом модели по каждой из i-х учитываемых переменных.
S2
|
Sy2 |
|
|
S42 |
|
S12 |
S32 |
|
S22 |
||
|
n
Рис. 1.9. Изменение составляющих ошибки с введением дополнительных переменных
Общая дисперсия ошибки у для некоррелированных входных воздействий:
s2y = s12 + s22 + s32 + s42.
Корреляцию входных воздействий можно учесть по известным формулам в каждом конкретном случае.
Нанесем на график (рис. 1.9) составляющие выражения s2y в зависимо-
сти от числа учитываемых переменных п. Конечно, характер кривых зависит от
конкретных свойств s2y , поэтому на рис.
1. 9 дана лишь принципиальная картина.
Дисперсия s21 уменьшается с увеличением числа переменных и стремится к нулю. Дисперсия s22 увеличивается с увеличением числа переменных, причем это увеличение тем меньше, чем меньше частная производная ∂f 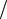 ∂xi . Диспер-
∂xi . Диспер-
сия s23 также возрастает с увеличением числа переменных, однако это увеличение не зависит от ∂f 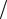 ∂xi , и существует, даже если ∂f
∂xi , и существует, даже если ∂f 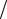 ∂xi =0. Дисперсия s24
∂xi =0. Дисперсия s24
также возрастает с увеличением числа переменных, причем ее возрастание зависит от свойств описываемой гиперповерхности и может быть как равным нулю, так и весьма большим. Например, при линейной модели, примененной для линейного объекта, s24=0, а для той же модели для многомерного параболоида с началом координат в его вершине s24 будет весьма большой.
В итоге общая дисперсия ошибки вначале падает, а затем начинает увеличиваться. Фактически это означает, что при некотором п использование информации о величине хп перестает приносить пользу, т. е. информация становится бесполезной, а затем и вредной. Именно так: получение и использование информации при определенных условиях может привести к увеличению средней квадратической погрешности расчетов у.
Найдем условия, при которых использование информации становится вредным. Это происходит тогда, когда для какого-либо i-гo признака
s22i + s32i > s12i .
В связи с невозможностью теоретической оценки погрешностей для
∂f ∂x покажем решение задачи для |
s2 |
|
: |
||||||||
i |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
i |
|
||
|
2 |
|
|
∂f |
|
2 |
|
|
|
∂f |
|
|
2 |
|
|
2 |
|
|
|
||||
( |
ai ) |
sxi |
∂x |
sxi |
или |
ai > |
∂x |
||||
> |
|
||||||||||
|
|
|
|
i |
|
|
|
|
i |
||
19
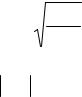
Следовательно, использование информации становится безусловно вредным, если ошибка в определении частной производной (коэффициентов уравнения) превышает ее величину. Именно поэтому незначимые коэффициенты модели лучше не использовать.
Учет s22 может только еще уменьшить найденную величину. Оценив ка- ким-либо путем, зависящим от метода получения модели, погрешность определения ее коэффициентов, можно сделать вывод о полезности включения соответствующего члена в уравнение модели.
Условие ai > ∂f 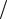 ∂xi предопределяет вредность использования дополни-
∂xi предопределяет вредность использования дополни-
тельной информации. Однако требования к точности определения коэффициентов ∂f 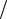 ∂xi значительно повысятся, если задаться точностью получаемой модели. До-
∂xi значительно повысятся, если задаться точностью получаемой модели. До-
пустим, 5 % – погрешность вычисления дисперсии s2y вследствие неточности коэффициентов модели. Тогда
n |
|
∑ ai2 sx2i |
= 0,05s2y . |
i=1 |
|
Если измерять переменные в долях среднего квадратического отклонения, то
n
∑ ai2 = 0,05.
i=1
Предположим, что погрешности определения всех коэффициентов одинаковы, тогда
a = |
0,05. |
i |
n |
|
т. е. например, при указанной точности для 10 параметров, учитываемых в моделях, ai = 0,07 . При измерении переменных в долях среднего квадратиче-
ского отклонения в случае корреляционной модели это соответствует доверительным интервалам частных коэффициентов корреляции.
Учет того факта, что введение дополнительных членов в уравнение может принести вред, позволит более строго подходить к построению модели и избежать возможного возрастания погрешностей модели.
1.4.7. Экспериментирование на модели и использование результатов
Для аналитических и алгоритмических моделей понятие экспериментирования на модели тождественно нахождению значений функции или выходной характеристики при интересующих значениях аргументов или входных переменных, т. е. подстановке в формулу или алгоритм конкретных чисел и расчету по формуле или алгоритму.
Перебор вариантов решения производится в пределах введенных ранее ограничений с заданным шагом варьирования. Результаты расчетов представляются в виде графиков или таблиц, а иногда и единственных требующихся значений.
20
