
глава1
.pdf1.МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ИМЕТОДЫ ИХ ПОЛУЧЕНИЯ
1.1. Основные понятия
Значение моделей в изучении мира отразил Дж. Форрестер: «Каждый индивидуум в своей личной и общественной жизни использует модели для принятия решения. Мысленный образ мира, окружающего нас, есть модель. Человек не несет в себе полных образов семьи, бизнеса, правительства, страны. Он только отбирает концепции и взаимосвязи, которые использует, чтобы представить себе реальную систему. Мысленный образ – это модель. Все наши решения и действия определяются моделями. Вопрос заключается не в том, использовать или игнорировать модели, а состоит только в выборе между альтернативными моделями».
Мысленный образ – одно из самых широких определение модели. В точных науках под моделью понимают формализуемый мысленный образ.
Модель является аналогом объекта, системы, процесса в некоторой форме, отличной от формы их реального существования Модель какого-либо объекта может быть или копией этого объекта выполненной из другого материала или в другом масштабе, либо отражать некоторую характерную совокупность параметров и свойств объекта в абстрактной форме. Хотя модели в научных и технических приложениях могут принимать разнообразные формы, но большую ценность благодаря универсальности имеют математические модели. Они дают совокупность соотношений между рассматриваемыми параметрами процессов в виде уравнений, алгоритмов и позволяют с определенной точностью описывать самый широкий спектр явлений: состояния, механические перемещения преобразования, химические превращения и т. д.
Моделирование – это процесс получения моделей реальной системы и постановки экспериментов на этой модели (решение на модели) с определенной целью.
Метод математического моделирования сводит исследование явлений внешнего мира к математическим задачам.
Математическое моделирование – один из эффективнейших методов исследования объектов. Часто с использованием моделирования получают новую информацию об исследуемом процессе. Иногда модель является единственным источникомтакойинформации.
Математическая модель должна быть пригодна для решения поставленной задачи, учитывать физические и математические ограничения и воспроизводить процесс с необходимой для исследователя точностью. Для описания любого объекта можно предложить множество моделей, отличающихся друг от друга в соответствии с поставленной целью моделирования.
Исследователь не решает задачу в чистом виде, каждый оперирует с моделью, котораяпостроена, исходяизпоставленнойзадачи.
Построениемоделииеепоследующееисследованиевыполняютдля:
• углубленного изучения механизма явления;
1
•прогноза поведения объекта;
•определения состояния, параметров, режимов системы;
•оптимизации процесса, аппарата, схемы;
•управлениясистемами;
•постановкиэксперимента;
•профессиональной подготовки и обучения;
•облегчения принятия решения в сложных ситуациях.
Искусством построения моделей можно овладеть только в результате собственной практики, однако почувствовать, в чем его суть, можно, разбирая примеры, которыеиллюстрируют различные особенности процесса моделирования.
Искусство моделирования состоит в способности анализировать проблему, выделять из нее путем абстракции ее существенные черты, выбирать и должным образом модифицировать основные предположения, характеризующие систему, а затемотрабатыватьисовершенствовать модель до тех пор, пока она не станет давать полезные для практики результаты. В. Т. Моррис формулирует следующие указания по искусству моделирования:
• разложить общую задачу исследования системы на ряд более простых
задач;
•четко сформулировать цели;
•подыскать аналогии;
•рассмотреть численный пример;
•выбрать определенные обозначения;
•записать очевидные соотношения;
•если полученная модель поддается математическому описанию, расширить ее, а в противном случае упростить.
1.2.Многообразие моделей
Впроцессе обучения каждый из нас многократно сталкивается с моделями
иприемами моделирования. Впервые это происходит при изучении физики, далее при изучении специальных дисциплин. Изучение теоретических основ, закономерностей любых процессов, анализ поведения объектов, выполнение большинства инженерных расчетов невозможно без использования разнообразных моде- лей-формул, систем уравнений, алгоритмов.
Любой из процессов может быть описан с самых разных сторон, В разной форме, с различной степенью детальности. Объект можно моделировать множеством способов в зависимости от того, что нас в объекте интересует. Элементы взаимосвязи должны быть выбраны так, чтобы было обеспечено выполнение специфическойзадачи, для которой собственно и формируется модель.
Рассмотрим лишь один конкретный процесс – флотацию. Упомянем некоторые из используемых моделей. Если для нас представляет интерес изменение извлечения минерала во времени, тоэтокинетическиеуравнения, есливконкретном исследовании необходимо использовать закономерности основного акта флотации, интерес будет представлять модель убыли свободной поверхностной энергии,
2
закономерности адсорбции реагентов на границе жидкость - воздух описывают уравнением Гиббса, для управленияпроцессомбольшеподойдутэкспериментально полученные физико-химические модели оптимальных концентраций реагентов А. А. Абрамова. Подчеркнем еще раз, что каждая из упомянутых моделей получена с определенной, представляющей для исследователя интерес, целью. С другой стороны, флотация – процесс многоэтапный, представляющий целую цепочку субпроцессов, не только связанных между собой вероятностными соотношениями, но и различными по физической сути. Поэтому для каждого из них целесообразно специфическое математическое описание. Однако даже один элементарный процесс может быть описан по-разному: во-первых, возможно его представление в различной математической форме, например, алгебраическое, дифференциальное, матричное уравнение, алгоритм функционирования и т.п., во-вторых, уже при выбранной форме уравнения не исключается разная степень детальности описания, отличия состоят в числе учитываемых факторов, параметров, порядке уравнения, учете взаимодействия факторов и т.д.
Какой конкретный вид должна иметь модель – определяется исследователем, ее использующим.
1.3. Классификация моделей
Существует несколько признаков классификации математических моделей. Некоторые из них и соответствующие им виды моделей приведены в табл. 1.1.
|
Таблица 1.1 |
|
Классификация моделей |
||
|
|
|
Признак классификации |
Виды моделей |
|
Характер отображаемых свойств |
Структурные: топологические, геометрические |
|
Функциональные |
||
|
||
|
Микроуровня |
|
Иерархический уровень |
Макроуровня |
|
|
Метауровня |
|
Степень детализации описания внутри |
Полные |
|
уровня |
Макромодели |
|
|
Статические |
|
Учет времени и действующих сил |
Кинетические |
|
|
Динамические |
|
Степень определенности параметров, ко- |
Детерминированные |
|
эффициентов, вида математического опи- |
||
Стохастические |
||
сания |
|
|
Способ представления свойств объекта |
Аналитические |
|
Алгоритмические |
||
(вид математического описания) |
||
Имитационные |
||
|
||
Способ получения модели |
Теоретические |
|
Эмпирические |
||
|
||
3
По характеру отображаемых свойств модели можно подразделить на структурные и функциональные.
Структурные математические модели делятся на топологические (отображают состав и связь элементов) и геометрические (несут информацию о геометрических свойствах объектов). В обогатительной технологии структура объектов часто задается разного рода схемами, примерами геометрических моделей в простейшем случае могут служить графики зависимостей, изображения аппаратов, чертежи зданий и тому подобная информация.
Функциональные математические модели предназначены для отображения физических или информационных процессов, протекающих в объекте. Это основной используемый в обогащении класс моделей.
Использование принципов блочно-иерархического подхода к моделированию объектов связано с возможностью их разбиения на элементы. Часто они представляют не простую структуру, состоящую из равнозначных элементов, а иерархиче-
скую. Под иерархической структурой понимается многоуровневая система, в кото-
рой определены отношения последовательной соподчинённости уровней. Сложная система (метауровень) может быть разбита на некоторое число крупных структурных образований – ячеек первого уровня (макроуровень). Каждая из них, в свою очередь, подразделяется на более мелкие ячейки второго уровня (микроуровень). Иерархическое представление структуры системы позволяет более детально описывать в моделях поведение отдельных составляющих и укрупнённо рассматривать моделиструктурныхобразованийболеевысокогоуровня.
Иерархическая структура применительно к моделям обогатительной технологии может рассматриваться в различных аспектах: временном, технологическом, масштабном. Например, процессы, происходящие в элементарных объемах обогатительных аппаратов, описываются моделями микроуровня, работа аппарата в целом может быть представлена моделью макроуровня, а для схемы, включающей множествоаппаратов, составляетсямодельметауровня.
Впределах каждого иерархического уровня по степени детализациивыделяют полные математические модели – переменные характеризуют состояние всех межэлементных связей и макромодели – часть связей опущена при укрупненном выделении элементов.
Математические модели бывают статические, кинетические, динамические. Статические модели y=f(x) определяют конечные, критические, равновесные значения параметров процесса, системы. К ним относятся модели состояния материала, связи входных х и выходных у переменных в установившихся режимах. Они могут быть представлены самыми разнообразными уравнениями: алгебраиче-
скими, дифференциальными, интегральными.
Вотличие от статических кинетические и динамические модели в качестве аргумента содержат время.
Кинетические модели y=f(x,t) или у=f[x, ϕ(t)] характеризуют течение процесса во времени и связывают их параметры со временем t. Их получают интегрированием дифференциальных уравнений при определенных начальных условиях.
4
Динамические модели y = f ( x , F , t ) описывают закономерности изменения состояния тел, масс под действием приложенных к ним сил F в различных средах. Основа описания – дифференциальные уравнения.
В теории управления процессами динамические модели характеризуют реакцию выходных показателей на стандартные возмущения на входе (реагентный режим, расходы, концентрации компонентов и фаз, свойств частиц и т.п.). Такие модели описываются системой дифференциальных уравнений.
Если входящие в модель параметры или входные переменные постоянны либо изменяются по вполне определенным, поддающимся точным измерениям закономерностям, то данная модель относится к классу детерминированных. По ней можно однозначно предсказать значения выходных величин по известным значениям входных.
Если отдельные параметры или входные переменные модели никогда не могут быть точно измерены и имеют случайный характер, модель является стохастической. Любое однократное решение на ней (реализация) даст случайный результат. Для получения приемлемых результатов моделирования в этом случае необходимы повторные решения для представительной выборки случайных величин.
Модель, содержащая стохастические переменные, должна, очевидно, описываться с использованием математического аппарата теории вероятностей и статистики.
По способу представления свойств объекта математические модели делят на:
аналитические – представляющие собой явные выражения выходных параметров как функции входных и внутренних параметров;
алгоритмические – выражающие связи выходных параметров с параметрами внутренними и внешними в форме алгоритма, в отличие от аналитического способа представления связывают входные и выходные переменные не явными выражениями, а последовательностью вычислительных процедур;
имитационные – вид алгоритмической модели, воспроизводящей последовательность событий в системе при вероятностном характере параметров системы; многократная имитация и статистическая обработка накопленных результатов позволяют оценить значения выходных параметров). Независимо от способа представления свойств объекта исследование модели и экспериментирование на ней выполняют обычно в численном виде.
Для получения математических моделей используют формальные и неформальные методы. Формальные методы применяют при известных моделях элементов отдельных составляющих объекта. Неформальные методы включают изучение закономерностей процессов и явлений, связанных с моделируемым объектом, выделение существенных факторов, принятие допущений и их обоснование. Неформальные методы применяют для получения математических моделей элементов системы. Этот этап наиболее ответственный, так как от него зависит эффективность модели (универсальность, точность, экономичность). Построение моделей элементов выполняется высококвалифицированным специалистом в данной предметной области и в вопросах математического моде-
5
лирования на ЭВМ. Неформальные методы можно использовать для синтеза теоретических и эмпирических математических моделей.
Модели получают двумя путями: теоретическим и экспериментальным. При строгом подходе почти любую модель вряд ли можно считать чисто теоретической, поскольку обычно она включает в себя параметры, которые определяются эмпирически самим исследователем или известны ему из прошлых экспериментов. Существенным в данном случае является вид деятельности, предшествующий получению конечного вида модели, аналитические рассуждения или эксперимент. Поэтому в дальнейшем будем разделять способы получения
моделей на аналитический (теоретиче-
ский) и экспериментальный, который может быть использован в различных вариантах в зависимости от способа по-
лучения информации об объекте. Следует заметить, что аналитиче-
ский путь применим для получения моделей создаваемых или даже несуществующих объектов. Он отличается глубоким проникновением в существо процесса и использованием, как правило, специфических предположений о явле-
ниях в описываемом процессе.
нет
бесполезны
1.4.Процесс моделирования
1.4.1.Основные этапы
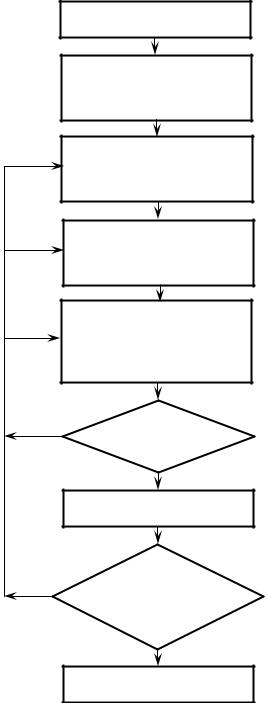
Процесс моделирования можно
разделить на несколько этапов (рис. 1.1). Первый из них – формулирование проблемы, когда на основе анализа имеющейся априорной информации и общей задачи уясняется цель моделирования.
На втором этапе вводятся границы решения задачи: конкретизируются ограничения по входным и внутренним переменным, вводятся критерии эффективности, задаются начальные и конечные условия.
Затем на основании обобщения фактов и явлений, введения упрощающих допущений качественные представления о связях между переменными реального объекта записываются в математических терминах – это этап формализации задачи.
6
Следующий этап – исследование математической задачи, к которой приводит математическое моделирование. В результате модель приводится к удобной для решения форме, выбирается метод решения и осуществляется само решение. В результате решений получают информацию (расчетные значения функции отклика – результаты вычислений по модели выходной переменной при известных значениях входных) для сопоставления с результатом наблюдения изучаемых явлений. Часто математические задачи, возникающие на основе различных математических моделей, бывают одинаковыми. В этом случае типичные математические задачи рассматривают как самостоятельный абстрактный объект.
Очередной этап – оценка адекватности моделей. Это проверка соответствия точности прогноза по гипотетической модели результатам наблюдения за моделируемой системой в тех же условиях. Если модель адекватна реальной системе, то она пригодна для последующего использования. В противном случае модель следует корректировать, начиная с любого из предыдущих этапов. Возможными путями достижения адекватности является сужение границ модели, учет дополнительных факторов – уточнение вида модели, использование большей информации об объекте, снижение формулируемых исследователем требований к точности.
После этого проводится экспериментирование на модели, накапливается информация для последующих решений.
Интерпретация (оценка полезности) модели связывает полученные путем моделирования результаты с достижением первоначально сформулированной цели моделирования. Если с помощью моделирования удается достичь поставленной цели, например, оптимизировать конструкцию аппарата, осуществлять прогноз в интересующих ситуациях, эффективно управлять процессом, то результаты используются. В противном случае проводят уточнение на любом из предыдущих этапов и процесс моделирования повторяется в новых условиях.
Эволюционный характер процесса конструирования модели неизбежен и желателен. По мере того, как достигаются цели и решаются поставленные задачи, ставятся новые задачи, либо возникает необходимость достижения большего соответствия между моделью и реальным объектом, что приводит к пересмотру модели и все лучшим ее реализациям. Это процесс, при котором начинают с построения простой модели, а затем в целом усложняют и улучшают ее.
1.4.2. Формулирование проблемы
Потребность получения модели какого-либо процесса возникает при решении какой-либо проблемы. В нашем случае она часто имеет конкретный характер. Модели создаются, если объект недостаточно изучен и не удается найти в практике попыток его формализации, либо если известные к настоящему времени модели в каком-то смысле не удовлетворяют исследователя. Например, модель не удовлетворяет требованиям точности, слишком сложна, не позволяет получить искомую информацию и т. д. То есть решение о составлении модели принимается уже после более или менее глубокого ознакомления с существом вопроса, областью знаний, в которой ведется исследование, возможными ана-
7
логами, и только в том случае, если возникает некая задача, не разрешимая известными методами. В противном случае всегда находятся готовые для использования модели v тогда решение сводится лишь к экспериментированию на модели.
На этапе формулирования проблемы в самом начале еще не ясно, надо ли разрабатывать новую модель или можно воспользоваться известной, либо вовсе обойтись без моделирования. Если изучение априорной информации показывает, что без создания модели не обойтись, надо весьма определенно сформулировать цель ее составления и использования. От обозначенной цели будет зависеть многое в дальнейшем процессе: форма представления модели, ее сложность, требуемая точность, методы моделирования. Модель может быть многоцелевой, например, совмещать в себе возможности получения новых закономерностей и прогноза поведения объекта. Модель может быть адаптируемой, то есть поэтапно трансформируемой по мере накопления наших знаний о существе вопроса.
Помимо уяснения цели желательно осуществить прогноз возможных результатов моделирования с тем, чтобы в дальнейшем целенаправленно вести анализ получаемых результатов.
Важнейшей составной частью этапа формулирования проблемы является накопление первичной информации о системе, которая может предопределить и математическую форму модели, и способ ее составления, и выбор методики оценки адекватности. Для полноты информации часто приходится прибегать к постановке специальных экспериментов, проясняющих взаимосвязь потенциальных переменных, уточняющих область существования и условия функционирования модели, а возможно и определяющих выбор экспериментального пути создания модели.
1.4.3. Введение допущений и ограничений
После формулирования проблемы моделирования для построения модели необходимо ввести допущения, позволяющие упростить реальную систему или облегчить последующее математическое решение задачи.
Математическая модель представляет собой упрощение реальной ситуации. Существенное упрощение наступает тогда, когда несущественные особенности ситуации отбрасываются и исходная сложная задача сводится к идеализированной задаче, поддающейся математическому анализу. Примерами упрощения в классической прикладной математике являются абсолютно жесткий удар, невязкие жидкости, блоки без трения и т.п. Эти понятия не соответствуют реальной действительности, они являются абстракциями, составной частью идеализации, предпринятой автором модели. Тем не менее, их часто можно считать хорошим приближением к реальным ситуациям.
В задачах обогащения допущения такого рода формулируются, например, таким образом: «сопротивлением воздуха движению частицы можно пренебречь», или «предположим, что частицы имеют сферическую форму», либо «допустим, что пузырьки воздуха во флотационной камере имеют одинаковый диаметр» и т. п.
8
Упростить модель в математическом плане можно одним из следующих способов:
•превратить переменные величины в константы;
•исключить некоторые переменные или объединить их;
•предположить линейную зависимость между исследуемыми величинами;
•ввести более жесткие предположения;
•наложить на систему более жесткие граничные условия.
Иной возможный подход состоит в постепенном «наращивании» модели, начиная с простейшей, отражающей наиболее характерные особенности явления. Затем эта простая модель обобщается, чтобы охватить другие факторы и получить «приемлемое» решение. Такой подход к модели, как к развивающейся системе, применим особенно в тех случаях, когда сама задача моделирования окончательно не сформулирована вначале и уточняется в ходе анализа.
Иногда допущения следуют из недостатка априорной информации об объекте, в других случаях они необходимы, чтобы упростить модель, обеспечить решение, сократить время моделирования. Однако следует помнить, что чрезмерные упрощения могут привести к потере точности модели, к уменьшению полноты получаемой информации. Корректность допущений впоследствии проверяется при оценке точности или адекватности модели. Кроме допущений, требуется оговорить накладываемые на модель ограничения, которые представляют собой возможные пределы изменения переменных. Они могут вводиться либо исследователем (искусственное ограничение), либо самим объектом вследствие присущих ему свойств (естественные ограничения). Искусственные ограничения могут быть технического или экономического характера; это, например, максимальная производительность аппарата, максимальная степень дробления за один прием, минимальная себестоимость переработки 1 тонны руды и т. п. Примерами естественных ограничений являются максимальное значение массовой доли компонента в руде, которая не может превышать значения массовой доли компонента в наиболее богатом минерале, или невозможность получения большей массы концентрата, чем масса переработанной руды. Следует заметить, что искусственные ограничения могут быть изменены, а естественные – нет.
Пределы изменения переменных модели, т. е. диапазон действия ограничений, могут влиять на вид приемлемой модели. Так, если возможные колебания переменных невелики, часто допустимо использование в качестве моделей линейных уравнений, уравнения же более высокого порядка существенного повышения точности не дают и поэтому особого смысла не имеют. С другой стороны, сужение ограничений ради упрощения вида уравнения не позволяет в дальнейшем исследовать модель в широком диапазоне изменения факторов, сужает область применения модели, поскольку вне области экспериментирования «поведение» объекта непредсказуемо (рис. 1.2). Чрезмерное расширение диапазона изменения переменных также имеет свои недостатки. Так, при пассивном эксперименте (наблюдение за процессом без вмешательства) увеличива-
9
ется время накопления необходимой информации об объекте, что связано с «ожиданием» редких ситуаций, а при активном пути (проведение эксперимента по плану с вмешательством в процесс), когда опыты ставятся на ограниченном числе уровней, возможны неправомерные упрощения вида модели, например: сложная функция может быть принята как линейная (рис. 1.3).
y=f1(x)
y
y=f2(x) y=f3(x)
Область x экспериментирования
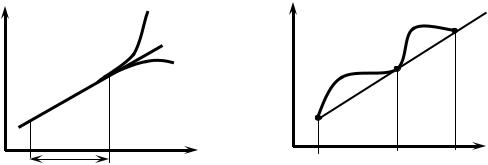
Рис. 1.2. Варианты поведения объекта вне области экспериментирования
y |
yм |
|
yр |
Точки экспериментирования x
Рис. 1.3. Неправомерное упрощение вида модели. Реальное поведение объекта yр не соответствует формально адекватной модели yм
1.4.4. Формализация модели и исследование математической задачи
Уяснение цели моделирования и накопление информации о предмете исследования позволяют выделить те элементы, которые войдут в модель, их количество. Под элементами следует понимать независимые переменные, параметры, коэффициенты, функциональные блоки (для имитационной модели) и т. д. Этот этап важен тем, что требуется найти компромисс между желанием учесть как можно большее число элементов и последствиями учета чрезмерного их числа. Простая модель, с одной стороны, легче понимается, анализируется, с другой – возможно, проигрывает в точности, не учитывает влияния какихто существенных факторов.
Когда принято решение об используемых элементах, желательно определить функциональные связи между ними, значения используемых параметров и коэффициентов. Часть такого рода информации получают постановкой специальных экспериментов, часть заимствуют из накопленного опыта, часть принимают интуитивно в виде гипотетических. Наконец, формализуя модель, требуется оговорить граничные, например, начальные и конечные, условия ее существования.
Для объектов, о поведении которых имеются ранее полученные сведения эмпирического характера или если им присущи общие законы, описанные для аналогичных процессов в других отраслях знаний, избирают теоретический путь построения моделей.
Процесс моделирования может быть существенно упрощен за счет накопления наборов готовых моделей и методов их использования, адаптации.
10
