
e-maxx_algo
.pdf
некоторые другие приложения дискретного преобразования Фурье.
Всевозможные суммы
Задача: даны два массива |
и . Требуется найти всевозможные числа вида |
, и для каждого такого |
||||
числа вывести количество способов получить его. |
|
|
||||
Например, для |
|
|
и |
получаем: число 3 можно получить 1 способом, 4 — также одним, 5 |
— 2, |
|
6 — 1, 7 — 1. |
|
|
|
|
|
|
Построим по массивам и |
два многочлена |
и . В качестве степеней в многочлене будут выступать сами числа, т. |
||||
е. значения |
( |
), а в качестве коэффициентов при них — сколько раз это число встречается в массиве ( ). |
|
|||
Тогда, перемножив эти два многочлена за |
, мы получим многочлен |
, где в качестве степеней |
|
|||
будут всевозможные числа вида |
, а коэффициенты при них будут как раз искомыми количествами |
|
||||
Всевозможные скалярные произведения
Даны два массива и одной длины  . Требуется вывести значения каждого скалярного произведения вектора
. Требуется вывести значения каждого скалярного произведения вектора  на очередной циклический сдвиг вектора
на очередной циклический сдвиг вектора  .
.
Инвертируем массив и припишем к нему в конец нулей, а к массиву — просто припишем самого себя. |
|
Затем перемножим их как многочлены. Теперь рассмотрим коэффициенты произведения |
(как |
всегда, все индексы в 0-индексации). Имеем: |
|
|
|
|
|
Поскольку все элементы  , то мы получаем:
, то мы получаем:
|
|
|
|
Нетрудно увидеть в этой сумме, что это именно скалярное произведение вектора на |
-ый |
||
циклический сдвиг. Таким образом, эти коэффициенты (начиная с |
-го и закачивая |
-ым) — и есть ответ |
|
на задачу. |
|
|
|
Решение получилось с асимптотикой |
. |
|
|
Две полоски
Даны две полоски, заданные как два булевских (т.е. числовых со значениями 0 или 1) массива и . Требуется
найти все такие позиции на первой полоске, что если приложить, начиная с этой позиции, вторую полоску, ни в каком месте не получится  сразу на обеих полосках. Эту задачу можно переформулировать таким образом: дана карта полоски, в виде 0/1 — можно вставать в эту клетку или нет, и дана некоторая фигурка в виде шаблона (в виде массива, в котором 0 — нет клетки, 1 — есть), требуется найти все позиции в полоске, к которым можно приложить фигурку.
сразу на обеих полосках. Эту задачу можно переформулировать таким образом: дана карта полоски, в виде 0/1 — можно вставать в эту клетку или нет, и дана некоторая фигурка в виде шаблона (в виде массива, в котором 0 — нет клетки, 1 — есть), требуется найти все позиции в полоске, к которым можно приложить фигурку.
Эта задача фактически ничем не отличается от предыдущей задачи — задачи о скалярном произведении. Действительно, скалярное произведение двух 0/1 массивов — это количество элементов, в которых одновременно оказались единицы. Наша задача в том, чтобы найти все циклические сдвиги второй полоски так, чтобы не нашлось ни одного элемента, в котором бы в обеих полосках оказались единицы. Т.е. мы должны найти все циклические сдвиги второго массива, при которых скалярное произведение равно нулю.
Таким образом, эту задачу мы решили за  .
.
Поиск в ширину
Поиск в ширину (обход в ширину, breadth-first search) — это один из основных алгоритмов на графах.
В результате поиска в ширину находится путь кратчайшей длины в невзвешененном графе, т.е. путь, содержащий наименьшее число рёбер.
Алгоритм работает за  , где
, где  — число вершин,
— число вершин,  — число рёбер.
— число рёбер.
Описание алгоритма
На вход алгоритма подаётся заданный граф (невзвешенный), и номер стартовой вершины  . Граф может быть как ориентированным, так и неориентированным, для алгоритма это не важно.
. Граф может быть как ориентированным, так и неориентированным, для алгоритма это не важно.
Сам алгоритм можно понимать как процесс "поджигания" графа: на нулевом шаге поджигаем только вершину  . На каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей; т.е. за одну итерацию алгоритма происходит расширение "кольца огня" в ширину на единицу (отсюда и название алгоритма).
. На каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей; т.е. за одну итерацию алгоритма происходит расширение "кольца огня" в ширину на единицу (отсюда и название алгоритма).
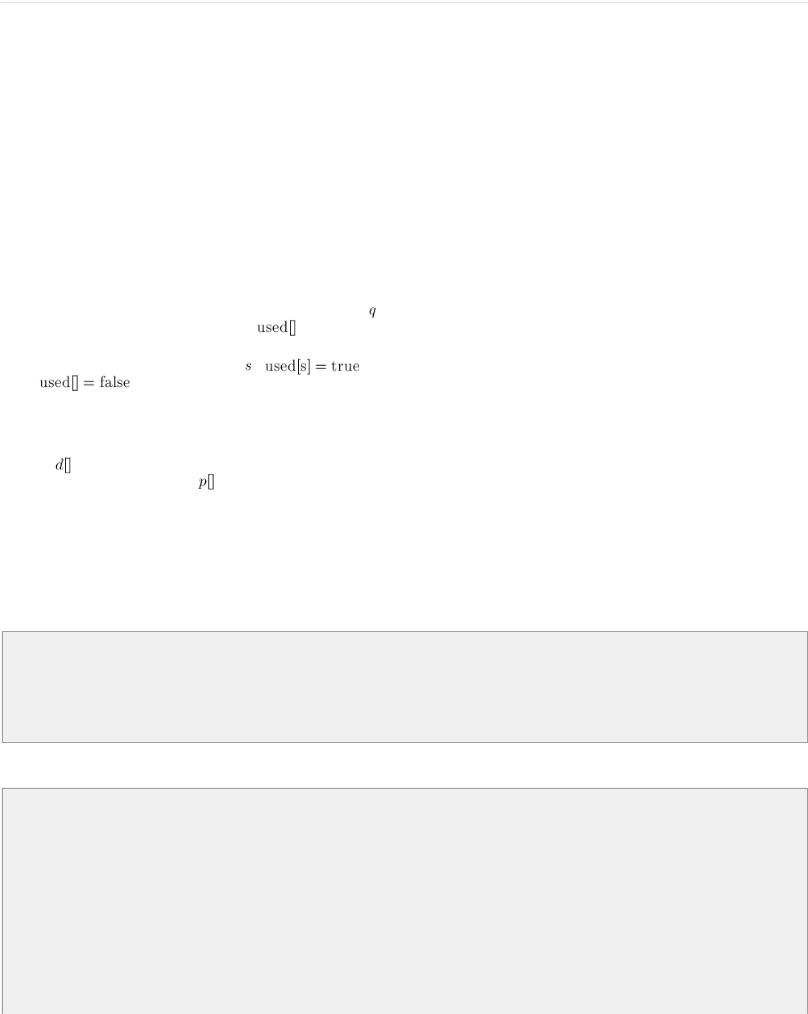
Более строго это можно представить следующим образом. Создадим очередь , в которую будут помещаться
горящие вершины, а также заведём булевский массив |
, в котором для каждой вершины будем отмечать, горит |
|
она уже или нет (или иными словами, была ли она посещена). |
|
|
Изначально в очередь помещается только вершина , и |
, а для всех остальных |
|
вершин |
. Затем алгоритм представляет собой цикл: пока очередь не пуста, достать из её головы |
|
одну вершину, просмотреть все рёбра, исходящие из этой вершины, и если какие-то из просмотренных вершин ещё не горят, то поджечь их и поместить в конец очереди.
В итоге, когда очередь опустеет, обход в ширину обойдёт все достижимые из  вершины, причём до каждой дойдёт кратчайшим путём. Также можно посчитать длины кратчайших путей (для чего просто надо завести массив длин путей ), и компактно сохранить информацию, достаточную для восстановления всех этих кратчайших путей
вершины, причём до каждой дойдёт кратчайшим путём. Также можно посчитать длины кратчайших путей (для чего просто надо завести массив длин путей ), и компактно сохранить информацию, достаточную для восстановления всех этих кратчайших путей
(для этого надо завести массив "предков" , в котором для каждой вершины хранить номер вершины, по которой мы попали в эту вершину).
Реализация
Реализуем вышеописанный алгоритм на языке C++. Входные данные:
vector < vector<int> > g; // граф int n; // число вершин
int s; // стартовая вершина (вершины везде нумеруются с нуля)
// чтение графа
...
Сам обход:
queue<int> q; q.push (s);
vector<bool> used (n);
vector<int> d (n), p (n); used[s] = true;
p[s] = -1;
while (!q.empty()) {
int v = q.front(); q.pop();
for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i];
if (!used[to]) { used[to] = true;
q.push (to);

d[to] = d[v] + 1; p[to] = v;
}
}
}
Если теперь надо восстановить и вывести кратчайший путь до какой-то вершины 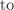 , это можно сделать следующим образом:
, это можно сделать следующим образом:
if (!used[to])
cout << "No path!";
else {
vector<int> path;
for (int v=to; v!=-1; v=p[v]) path.push_back (v);
reverse (path.begin(), path.end()); cout << "Path: ";
for (size_t i=0; i<path.size(); ++i) cout << path[i] + 1 << " ";
}
Приложения алгоритма
●Поиск кратчайшего пути в невзвешенном графе.
●Поиск компонент связности в графе за  .
.
Для этого мы просто запускаем обход в ширину от каждой вершины, за исключением вершин, оставшихся
посещёнными ( |
) после предыдущих запусков. Таким образом, мы выполняем обычный запуск в ширину |
||
от каждой вершины, но не обнуляем каждый раз массив |
, за счёт чего мы каждый раз будем обходить |
||
новую компоненту связности, а суммарное время работы алгоритма составит по-прежнему |
(такие |
||
несколько запусков обхода на графе без обнуления массива |
называются серией обходов в ширину). |
||
●Нахождения решения какой-либо задачи (игры) с наименьшим числом ходов, если каждое состояние системы можно представить вершиной графа, а переходы из одного состояния в другое — рёбрами графа.
Классический пример — игра, где робот двигается по полю, при этом он может передвигать ящики, находящиеся на этом же поле, и требуется за наименьшее число ходов передвинуть ящики в требуемые позиции. Решается это обходом
в ширину по графу, где состоянием (вершиной) является набор координат: координаты робота, и координаты всех коробок.
●Нахождение кратчайшего пути в 0-1-графе (т.е. графе взвешенном, но с весами равными только 0 либо 1): достаточно немного модифицировать поиск в ширину: если текущее ребро нулевого веса, и происходит улучшение расстояния до какой-то вершины, то эту вершину добавляем не в конец, а в начало очереди.
●Нахождение кратчайшего цикла в неориентированном невзвешенном графе: производим поиск в ширину из каждой вершины; как только в процессе обхода мы пытаемся пойти из текущей вершины по какому-то ребру в уже посещённую вершину, то это означает, что мы нашли кратчайший цикл, и останавливаем обход в ширину; среди всех таких найденных циклов (по одному от каждого запуска обхода) выбираем кратчайший.
● |
Найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин |
. |
||||||
|
Для этого надо запустить 2 поиска в ширину: из |
, и из |
. Обозначим через |
массив кратчайших |
|
|||
|
расстояний, полученный в результате первого обхода, а через |
— в результате второго обхода. Теперь для |
|
|||||
|
любого ребра |
легко проверить, лежит ли он на каком-либо кратчайшем пути: критерием будет |
|
|||||
|
условие |
|
. |
|
|
|
|
|
● |
Найти все вершины, лежащие на каком-либо кратчайшем пути между заданной парой вершин |
. |
||||||
|
Для этого надо запустить 2 поиска в ширину: из |
, и из |
. Обозначим через |
массив кратчайших |
|
|||
|
расстояний, полученный в результате первого обхода, а через |
— в результате второго обхода. Теперь для |
|
|||||
|
любой вершины |
легко проверить, лежит ли он на каком-либо кратчайшем пути: критерием будет |
|
|||||
|
условие |
|
. |
|
|
|
|
|
● |
Найти кратчайший чётный путь в графе (т.е. путь чётной длины). Для этого надо построить |
|
||||||
|
вспомогательный граф, вершинами которого будут состояния |
, где — номер текущей вершины, |
|
|||||
|
— текущая чётность. Любое ребро |
исходного графа в этом новом графе превратится в два |
|
|||||
|
ребра |
и |
. После этого на этом графе надо обходом в ширину найти кратчайший |
|||||
путь из стартовой вершины в конечную, с чётностью, равной 0.
Задачи в online judges
Список задач, которые можно сдать, используя обход в ширину: ● SGU #213 "Strong Defence" [сложность: средняя]

Поиск в глубину
Это один из основных алгоритмов на графах.
В результате поиска в глубину находится лексикографически первый путь в графе. Алгоритм работает за O (N+M).
Применения алгоритма
●Поиск любого пути в графе.
●Поиск лексикографически первого пути в графе.
●Проверка, является ли одна вершина дерева предком другой:
В начале и конце итерации поиска в глубину будет запоминать "время" захода и выхода в каждой вершине. Теперь за O
(1) можно найти ответ: вершина i является предком вершины j тогда и только тогда, когда starti < startj и endi > endj.
●Задача LCA (наименьший общий предок).
●Топологическая сортировка:
Запускаем серию поисков в глубину, чтобы обойти все вершины графа. Отсортируем вершины по времени выхода по убыванию - это и будет ответом.
●Проверка графа на ацикличность и нахождение цикла
●Поиск компонент сильной связности:
Сначала делаем топологическую сортировку, потом транспонируем граф и проводим снова серию поисков в глубину в порядке, определяемом топологической сортировкой. Каждое дерево поиска - сильносвязная компонента.
●Поиск мостов:
Сначала превращаем граф в ориентированный, делая серию поисков в глубину, и ориентируя каждое ребро так, как мы пытались по нему пройти. Затем находим сильносвязные компоненты. Мостами являются те рёбра, концы которых принадлежат разным сильносвязным компонентам.
Реализация
vector < vector<int> > g; // граф int n; // число вершин
vector<int> color; // цвет вершины (0, 1, или 2)
vector<int> time_in, time_out; // "времена" захода и выхода из вершины int dfs_timer = 0; // "таймер" для определения времён
void dfs (int v) {
time_in[v] = dfs_timer++; color[v] = 1;
for (vector<int>::iterator i=g[v].begin(); i!=g[v].end(); ++i) if (color[*i] == 0)
dfs (*i);
color[v] = 2;
time_out[v] = dfs_timer++;
}
Это наиболее общий код. Во многих случаях времена захода и выхода из вершины не важны, так же как и не важны цвета вершин (но тогда надо будет ввести аналогичный по смыслу булевский массив used). Вот наиболее
простая реализация:
vector < vector<int> > g; // граф int n; // число вершин
vector<char> used;
void dfs (int v) { used[v] = true;
for (vector<int>::iterator i=g[v].begin(); i!=g[v].end(); ++i) if (!used[*i])
dfs (*i);
}

Топологическая сортировка
Дан ориентированный граф с  вершинами и
вершинами и  рёбрами. Требуется перенумеровать его вершины таким образом, чтобы каждое рёбро вело из вершины с меньшим номером в вершину с большим.
рёбрами. Требуется перенумеровать его вершины таким образом, чтобы каждое рёбро вело из вершины с меньшим номером в вершину с большим.
Иными словами, требуется найти перестановку вершин (топологический порядок), соответствующую порядку, задаваемому всеми рёбрами графа.
Топологическая сортировка может быть не единственной (например, если граф — пустой; или если есть три такие вершины  ,
,  ,
,  , что из
, что из  есть пути в
есть пути в  и в
и в  , но ни из
, но ни из  в
в  , ни из
, ни из  в
в  добраться нельзя).
добраться нельзя).
Топологической сортировки может не существовать вовсе — если граф содержит циклы (поскольку при этом возникает противоречие: есть путь и из одной вершины в другую, и наоборот).
Распространённая задача на топологическую сортировку — следующая. Есть  переменных, значения которых нам неизвестны. Известно лишь про некоторые пары переменных, что одна переменная меньше другой. Требуется проверить, не противоречивы ли эти неравенства, и если нет, выдать переменные в порядке их возрастания (если решений несколько — выдать любое). Легко заметить, что это в точности и есть задача о поиске топологической сортировки в графе из
переменных, значения которых нам неизвестны. Известно лишь про некоторые пары переменных, что одна переменная меньше другой. Требуется проверить, не противоречивы ли эти неравенства, и если нет, выдать переменные в порядке их возрастания (если решений несколько — выдать любое). Легко заметить, что это в точности и есть задача о поиске топологической сортировки в графе из  вершин.
вершин.
Алгоритм
Для решения воспользуемся обходом в глубину.
Предположим, что граф ацикличен, т.е. решение существует. Что делает обход в глубину? При запуске из какойто вершины  он пытается запуститься вдоль всех рёбер, исходящих из
он пытается запуститься вдоль всех рёбер, исходящих из  . Вдоль тех рёбер, концы которых уже были посещены ранее, он не проходит, а вдоль всех остальных — проходит и вызывает себя от их концов.
. Вдоль тех рёбер, концы которых уже были посещены ранее, он не проходит, а вдоль всех остальных — проходит и вызывает себя от их концов.
Таким образом, к моменту выхода из вызова все вершины, достижимые из  как непосредственно (по
как непосредственно (по
одному ребру), так и косвенно (по пути) — все такие вершины уже посещены обходом. Следовательно, если мы будем в момент выхода из добавлять нашу вершину в начало некоего списка, то в конце концов в этом списке
получится топологическая сортировка.
Эти объяснения можно представить и в несколько ином свете, с помощью понятия "времени выхода" обхода в глубину. Время выхода для каждой вершины  — это момент времени, в который закончил работать вызов
— это момент времени, в который закончил работать вызов
обхода в глубину от неё (времена выхода можно занумеровать от  до
до  ). Легко понять, что при обходе в
). Легко понять, что при обходе в
глубину время выхода из какой-либо вершины |
всегда больше, чем время выхода из всех вершин, достижимых из неё |
(т.к. они были посещены либо до вызова |
, либо во время него). Таким образом, искомая |
топологическая сортировка — это сортировка в порядке убывания времён выхода.
Реализация
Приведём реализацию, предполагающую, что граф ацикличен, т.е. искомая топологическая сортировка существует. При необходимости проверку графа на ацикличность легко вставить в обход в глубину, как описано в статье по обходу
вглубину.
int n; // число вершин vector<int> g[MAXN]; // граф bool used[MAXN];
vector<int> ans; void dfs (int v) {
used[v] = true;
for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i];
if (!used[to]) dfs (to);
}
ans.push_back (v);
}
void topological_sort() {
for (int i=0; i<n; ++i) used[i] = false;
ans.clear();

for (int i=0; i<n; ++i) if (!used[i])
dfs (i);
reverse (ans.begin(), ans.end());
}
Здесь константе  следует задать значение, равное максимально возможному числу вершин в графе.
следует задать значение, равное максимально возможному числу вершин в графе.
Основная функция решения — это topological_sort, она инициализирует пометки обхода в глубину, запускает его, и ответ в итоге получается в векторе  .
.
Задачи в online judges
Список задач, в которых требуется искать топологическую сортировку:
● |
UVA #10305 "Ordering Tasks" |
[сложность: низкая] |
● |
UVA #124 "Following Orders" |
[сложность: низкая] |
● |
UVA #200 "Rare Order" [сложность: низкая] |
|

Алгоритм поиска компонент связности в графе
Дан неориентированный граф с  вершинами и
вершинами и  рёбрами. Требуется найти в нём все компоненты связности, т. е. разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами — пути не существует.
рёбрами. Требуется найти в нём все компоненты связности, т. е. разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами — пути не существует.
Алгоритм решения
Для решения можно воспользоваться как обходом в глубину, так и обходом в ширину.
Фактически, мы будем производить серию обходов: сначала запустим обход из первой вершины, и все вершины, которые он при этом обошёл — образуют первую компоненту связности. Затем найдём первую из оставшихся вершин, которые ещё не были посещены, и запустим обход из неё, найдя тем самым вторую компоненту связности. И так далее, пока все вершины не станут помеченными.
Итоговая асимптотика составит |
: в самом деле, такой алгоритм не будет запускаться от одной и той |
же вершины дважды, а, значит, каждое ребро будет просмотрено ровно два раза (с одного конца и с другого конца).
Реализация
Для реализации чуть более удобным является обход в глубину:
int n;
vector<int> g[MAXN]; bool used[MAXN]; vector<int> comp;
void dfs (int v) { used[v] = true;
comp.push_back (v);
for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i];
if (! used[to]) dfs (to);
}
}
void find_comps() {
for (int i=0; i<n; ++i) used[i] = false;
for (int i=0; i<n; ++i) if (! used[i]) {
comp.clear(); dfs (i);
cout << "Component:";
for (size_t j=0; j<comp.size(); ++j) cout << ' ' << comp[j];
cout << endl;
}
}
Основная функция для вызова —  , она находит и выводит компоненты связности графа.
, она находит и выводит компоненты связности графа.
Мы считаем, что граф задан списками смежности, т.е. содержит список вершин, в которые есть рёбра из вершины
 . Константе
. Константе 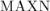 следует задать значение, равное максимально возможному количеству вершин в графе. Вектор
следует задать значение, равное максимально возможному количеству вершин в графе. Вектор  содержит список вершин в текущей компоненте связности.
содержит список вершин в текущей компоненте связности.

Поиск компонент сильной связности, построение конденсации графа
Определения, постановка задачи
Дан ориентированный граф , множество вершин которого и множество рёбер — . Петли и кратные рёбра допускаются. Обозначим через  количество вершин графа, через
количество вершин графа, через  — количество рёбер.
— количество рёбер.
Компонентой сильной связности (strongly connected component) называется такое (максимальное
по включению) подмножество вершин , что любые две вершины этого подмножества достижимы друг из друга, т.е.
для |
|
|
: |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
||||||||
где символом |
|
здесь и далее мы будем обозначать достижимость, т.е. существование пути из первой вершины |
||||||||
во вторую. |
|
|
|
|
|
|
|
|
|
|
Понятно, что компоненты сильной связности для данного графа не пересекаются, т.е. фактически это разбиение |
||||||||||
всех вершин графа. Отсюда логично определение конденсации |
как графа, получаемого из данного |
|||||||||
графа сжатием каждой компоненты сильной связности в одну вершину. Каждой вершине графа конденсации |
|
|||||||||
соответствует компонента сильной связности графа |
, а ориентированное ребро между двумя вершинами |
и |
||||||||
графа конденсации проводится, если найдётся пара вершин |
|
, между которыми существовало ребро |
||||||||
в исходном графе, т.е. |
. |
|
|
|
|
|
|
|||
Важнейшим свойством графа конденсации является то, что он ацикличен. Действительно, предположим, |
|
|||||||||
что |
|
, докажем, что |
|
. Из определения конденсации получаем, что найдутся две вершины |
|
|||||
и |
, что |
. Доказывать будем от противного, т.е. предположим, что |
, тогда найдутся две |
|||||||
вершины |
|
|
и |
, что |
. Но т.к. |
и |
находятся в одной компоненте сильной связности, то |
|||
между ними есть путь; аналогично для |
и . В итоге, объединяя пути, получаем, что |
, и одновременно |
||||||||
. Следовательно, и |
должны принадлежать одной компоненте сильной связности, т.е. получили |
|
||||||||
противоречие, что и требовалось доказать. |
|
|
|
|
|
|||||
Описываемый ниже алгоритм выделяет в данном графе все компоненты сильной связности. Построить по ним граф конденсации не составит труда.
Алгоритм
Описываемый здесь алгоритм был предложен независимо Косараю (Kosaraju) и Шариром (Sharir) в 1979 г. Это очень простой в реализации алгоритм, основанный на двух сериях поисков в глубину, и потому работающий за
время  .
.
На первом шаге алгоритма выполняется серия обходов в глубину, посещающая весь граф. Для этого мы проходимся по всем вершинам графа и из каждой ещё не посещённой вершины вызываем обход в глубину. При
этом для каждой вершины запомним время выхода |
. Эти времена выхода играют ключевую роль |
|||
в алгоритме, и эта роль выражена в приведённой ниже теореме. |
|
|||
Сначала введём обозначение: время выхода |
из компоненты сильной связности определим как максимум |
|||
из значений |
для всех |
. Кроме того, в доказательстве теоремы будут упоминаться и времена входа |
||
в каждую вершину |
, и аналогично определим времена входа |
для каждой компоненты сильной |
||
связности как минимум из величин 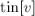 для всех
для всех  .
.
Теорема. Пусть и |
— две различные компоненты сильной связности, и пусть в графе конденсации между |
||||
ними есть ребро |
. Тогда |
. |
|
|
|
При доказательстве возникает два принципиально различных случая в зависимости от того, в какую из компонент |
|||||
первой зайдёт обход в глубину, т.е. в зависимости от соотношения между |
и |
|
: |
||
● Первой была достигнута компонента . Это означает, что в какой-то момент времени обход в глубину заходит |
|||||
в некоторую вершину |
компоненты , при этом все остальные вершины компонент |
и |
ещё не посещены. Но, т.к. |
||
по условию в графе конденсаций есть ребро |
, то из вершины |
будет достижима не только вся компонента , |
|||
но и вся компонента |
. Это означает, что при запуске из вершины обход в глубину пройдёт по всем |
||||
вершинам компонент |
и , а, значит, они станут потомками по отношению к в дереве обхода в глубину, т.е. |
||||
для любой вершины |
|
будет выполнено |
|
, ч.т.д. |
|
● Первой была достигнута компонента  . Опять же, в какой-то момент времени обход в глубину заходит в
. Опять же, в какой-то момент времени обход в глубину заходит в

некоторую вершину |
, причём все остальные вершины компонент |
и |
не посещены. Поскольку по условию |
|
в графе конденсаций существовало ребро |
, то, вследствие ацикличности графа конденсаций, не |
|||
существует обратного пути |
, т.е. обход в глубину из вершины |
не достигнет вершин . Это означает, что |
||
они будут посещены обходом в глубину позже, откуда и следует |
|
, ч.т.д. |
||
Доказанная теорема является основой алгоритма поиска компонент сильной связности. Из неё следует,
что любое ребро |
в графе конденсаций идёт из компоненты с большей величиной |
в компоненту с |
|
меньшей величиной. |
|
|
|
Если мы отсортируем все вершины |
в порядке убывания времени выхода |
, то первой окажется |
|
некоторая вершина  , принадлежащая "корневой" компоненте сильной связности, т.е. в которую не входит ни одно ребро в графе конденсаций. Теперь нам хотелось бы запустить такой обход из этой вершины
, принадлежащая "корневой" компоненте сильной связности, т.е. в которую не входит ни одно ребро в графе конденсаций. Теперь нам хотелось бы запустить такой обход из этой вершины  , который бы посетил только эту компоненту сильной связности и не зашёл ни в какую другую; научившись это делать, мы сможем постепенно выделить все компоненты сильной связности: удалив из графа вершины первой выделенной компоненты, мы снова найдём среди оставшихся вершину с наибольшей величиной
, который бы посетил только эту компоненту сильной связности и не зашёл ни в какую другую; научившись это делать, мы сможем постепенно выделить все компоненты сильной связности: удалив из графа вершины первой выделенной компоненты, мы снова найдём среди оставшихся вершину с наибольшей величиной  , снова запустим из неё этот обход, и т.д.
, снова запустим из неё этот обход, и т.д.
Чтобы научиться делать такой обход, рассмотрим транспонированный граф |
, т.е. граф, полученный из |
|
изменением направления каждого ребра на противоположное. Нетрудно понять, что в этом графе будут те |
||
же компоненты сильной связности, что и в исходном графе. Более того, граф конденсации |
для него |
|
будет равен транспонированному графу конденсации исходного графа |
. Это означает, что теперь |
|
из рассматриваемой нами "корневой" компоненты уже не будут выходить рёбра в другие компоненты.
Таким образом, чтобы обойти всю "корневую" компоненту сильной связности, содержащую некоторую вершину
 , достаточно запустить обход из вершины
, достаточно запустить обход из вершины  в графе . Этот обход посетит все вершины этой компоненты
в графе . Этот обход посетит все вершины этой компоненты
сильной связности и только их. Как уже говорилось, дальше мы можем мысленно удалить эти вершины из графа, находить очередную вершину с максимальным значением и запускать обход на транспонированном графе
из неё, и т.д.
Итак, мы построили следующий алгоритм выделения компонент сильной связности:
1 шаг. Запустить серию обходов в глубину графа , которая возвращает вершины в порядке увеличения времени
выхода |
, т.е. некоторый список |
. |
|
2 шаг. Построить транспонированный граф |
. Запустить серию обходов в глубину/ширину этого графа в |
||
порядке, определяемом списком |
(а именно, в обратном порядке, т.е. в порядке уменьшения времени |
||
выхода). Каждое множество вершин, достигнутое в результате очередного запуска обхода, и будет очередной |
|||
компонентой сильной связности. |
|
|
|
Асимптотика алгоритма, очевидно, равна |
, поскольку он представляет собой всего лишь два обхода |
||
в глубину/ширину. |
|
|
|
Наконец, уместно отметить связь с понятием топологической сортировки. Во-первых, шаг 1
алгоритма представляет собой не что иное, как топологическую сортировку графа (фактически именно это и означает сортировка вершин по времени выхода). Во-вторых, сама схема алгоритма такова, что и компоненты сильной связности он генерирует в порядке уменьшения их времён выхода, таким образом, он генерирует компоненты - вершины графа конденсации в порядке топологической сортировки.
Реализация
vector < vector<int> > g, gr; vector<char> used; vector<int> order, component;
void dfs1 (int v) { used[v] = true;
for (size_t i=0; i<g[v].size(); ++i) if (!used[ g[v][i] ])
dfs1 (g[v][i]); order.push_back (v);
}
void dfs2 (int v) { used[v] = true;
component.push_back (v);
for (size_t i=0; i<gr[v].size(); ++i) if (!used[ gr[v][i] ])
dfs2 (gr[v][i]);
}
int main() {
