e-maxx_algo

Реализация алгоритма Гарнера

Удобнее всего реализовывать этот алгоритм на языке Java, поскольку она содержит стандартную длинную арифметику, а потому не возникает никаких проблем с переводом числа из модульной системы в обычное число

(используется стандартный класс BigInteger).

Приведённая ниже реализация алгоритма Гарнера поддерживает сложение, вычитание и умножение, причём поддерживает работу с отрицательными числами (об этом см. пояснения после кода). Реализован перевод числа обычного десятичкого представления в модулярную систему и наоборот.

В данном примере берутся простых после , что позволяет работать с числами до примерно .

final int SZ = 100;

int pr[] = new int[SZ];

int r[][] = new int[SZ][SZ];

void init() {

for (int x=1000*1000*1000, i=0; i<SZ; ++x)

if (BigInteger.valueOf(x).isProbablePrime(100)) pr[i++] = x;

for (int i=0; i<SZ; ++i)

for (int j=i+1; j<SZ; ++j)

r[i][j] = BigInteger.valueOf( pr[i] ).modInverse( BigInteger.valueOf( pr

[j] ) ).intValue();

}

class Number {

int a[] = new int[SZ];

public Number() {

}

public Number (int n) {

for (int i=0; i<SZ; ++i) a[i] = n % pr[i];

}

public Number (BigInteger n) {

for (int i=0; i<SZ; ++i)

a[i] = n.mod( BigInteger.valueOf( pr

[i] ) ).intValue();

}

public Number add (Number n) {

Number result = new Number();

for (int i=0; i<SZ; ++i)

result.a[i] = (a[i] + n.a[i]) % pr[i]; return result;

}

public Number subtract (Number n) { Number result = new Number();

for (int i=0; i<SZ; ++i)

result.a[i] = (a[i] - n.a[i] + pr[i]) % pr[i]; return result;

}

public Number multiply (Number n) { Number result = new Number();

for (int i=0; i<SZ; ++i)

result.a[i] = (int)( (a[i] * 1l * n.a[i]) %

pr[i] );

return result;

}

public BigInteger bigIntegerValue (boolean can_be_negative) {

BigInteger result = BigInteger.ZERO, mult = BigInteger.ONE;

int x[] = new int[SZ]; for (int i=0; i<SZ; ++i) {

x[i] = a[i];

for (int j=0; j<i; ++j) {

long cur = (x[i] - x[j]) * 1l * r[j][i]; x[i] = (int)( (cur % pr[i] + pr[i]) %

pr[i] );

}

result = result.add( mult.multiply ( BigInteger.valueOf( x[i] ) ) );

mult = mult.multiply( BigInteger.valueOf

( pr[i] ) );

}

if (can_be_negative)

if (result.compareTo( mult.shiftRight(1) ) >= 0) result = result.subtract( mult );

иотрицательными числами. Однако можно заметить, что, если в конкретной задаче ответ по модулю не превосходит половины от произведения всех простых, то положительные числа будут отличаться от отрицательных тем, что положительные числа получатся меньше этой середины, а отрицательные — больше. Поэтому мы после классического алгоритма Гарнера сравниваем результат с серединой, и если он больше, то выводим минус,

иинвертируем результат (т.е. отнимаем его от произведения всех простых, и выводим уже его).

Нахождение степени делителя факториала

Даны два числа: и . Требуется посчитать, с какой степенью делитель входит в число , т.е. найти наибольшее такое, что делится на .

Решение для случая простого

Рассмотрим сначала случай, когда простое. Выпишем выражение для факториала в явном виде:

И так далее, каждый -ый член ряда даёт +1 к ответу, а количество таких членов равно 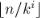. Таким образом, ответ равен величине:

Реализация:

int fact_pow (int n, int k) { int res = 0;

while (n) {

n /= k; res += n;

}

return res;

}

Решение для случая составного

Ту же идею применить здесь непосредственно уже нельзя.

Но мы можем факторизовать , решить задачу для каждого его простого делителя, а потом выбрать минимум из ответов. Более формально, пусть — это -ый делитель числа , входящий в него в степени . Решим задачу для с

Учитывая, что факторизация простейшим образом выполняется за , получаем итоговую асимптотику .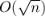

Троичная сбалансированная система счисления

Троичная сбалансированная система счисления — это нестандартная позиционная система счисления. Основание системы равно , однако она отличается от обычной троичной системы тем, что цифрами являются

. Поскольку использовать для одной цифры очень неудобно, то обычно принимают какое-то специальное обозначение. Условимся здесь обозначать минус единицу буквой .

Например, число в троичной сбалансированной системе записывается как , а число — как . Троичная сбалансированная система счисления позволяет записывать отрицательные числа без записи отдельного

знака "минус". Троичная сбалансированная система позволяет дробные числа (например, записывается как ).

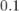Алгоритм перевода

Научимся переводить числа в троичную сбалансированную систему. Для этого надо сначала перевести число в троичную систему.

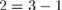Ясно, что теперь нам надо избавиться от цифр , для чего заметим, что , т.е. мы можем заменить двойку в текущем разряде на , при этом увеличив следующий (т.е. слева от него в естественной записи) разряд на . Если мы будем двигаться по записи справа налево и выполнять вышеописанную операцию (при этом в каких-то разрядах может происходить переполнение больше , в таком случае, естественно, "сбрасываем" лишние тройки в старший разряд), то придём к троичной сбалансированной записи. Как нетрудно убедиться, то же самое правило верно и для дробных чисел.

Более изящно вышеописанную процедуру можно описать так. Мы берём число в троичной системе счисления, прибавляем к нему бесконечное число , а затем от каждого разряда результата отнимаем единицу (уже безо всяких переносов).

Зная теперь алгоритм перевода из обычной троичной системы в сбалансированную, легко можно реализовать операции сложения, вычитания и деления — просто сводя их к соответствующим операциям над троичными несбалансированными числами.

Вычисление факториала по модулю

В некоторых случаях необходимо считать по некоторому простому модулю сложные формулы, которые в том числе могут содержать факториалы. Здесь мы рассмотрим случай, когда модуль сравнительно мал. Понятно, что эта задача имеет смысл только в том случае, когда факториалы входят и в числитель, и в знаменатель дробей. Действительно, факториал и все последующие обращаются в ноль по модулю , однако в дробях

все множители, содержащие , могут сократиться, и полученное выражение уже будет отлично от нуля по модулю .

Таким образом, формально задача такая. Требуется вычислить по простому модулю , при этом не учитывая все кратные 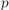множители, входящие в факториал. Научившись эффективно вычислять такой факториал, мы сможем быстро вычислять значение различных комбинаторных формул (например, Биномиальные коэффициенты).

Алгоритм

Выпишем этот "модифицированный" факториал в явном виде:

При такой записи видно, что "модифицированный" факториал распадается на несколько блоков длины (последний блок, возможно, короче), которые все одинаковы, за исключением последнего элемента:

(см. Бинарное возведение в степень; впрочем, можно заметить, что мы фактически возводим минус единицу в какую-

глубина рекурсии будет , итого асимптотика алгоритма получается .

Реализация

Понятно, что при реализации не обязательно использовать рекурсию в явном виде: поскольку рекурсия хвостовая, её легко развернуть в цикл.

int factmod (int n, int p) { int res = 1;

while (n > 1) {

res = (res * ((n/p) % 2 ? p-1 : 1)) % p; for (int i=2; i<=n%p; ++i)

res = (res * i) % p;

n /= p;

}

return res % p;

}

Эта реализация работает за .

Перебор всех подмасок данной маски

Перебор подмасок фиксированной маски

Дана битовая маска . Требуется эффективно перебрать все её подмаски, т.е. такие маски , в которых могут быть включены только те биты, которые были включены в маске .

Сразу рассмотрим реализацию этого алгоритма, основанную на трюках с битовыми операциями:

int s = m; while (s > 0) {

... можно использовать s ...

s = (s-1) & m;

}

или, используя более компактный оператор :

for (int s=m; s; s=(s-1)&m)

... можно использовать s ...

Единственное исключение для обоих вариантов кода — подмаска, равная нулю, обработана не будет. Её обработку придётся выносить из цикла, или использовать менее изящную конструкцию, например:

for (int s=m; ; s=(s-1)&m) {

... можно использовать s ...

if (s==0) break;

}

Разберём, почему приведённый выше код действительно находит все подмаски данной маски, причём без повторений, за O (их количества), и в порядке убывания.

Пусть у нас есть текущая подмаска , и мы хотим перейти к следующей подмаске. Отнимем от маски единицу, тем самым мы снимем самый правый единичный бит, а все биты правее него поставятся в . Затем удалим все "лишние" единичные биты, которые не входят в маску и потому не могут входить в подмаску. Удаление осуществляется битовой операцией . В результате мы "обрежем" маску до того наибольшего значения, которое она может принять, т.е. до следующей подмаски после в порядке убывания.

Таким образом, этот алгоритм генерирует все подмаски данной маски в порядке строгого убывания, затрачивая на каждый переход по две элементарные операции.

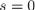не что иное, как маска . Поэтому с маской следует быть осторожным — если вовремя не остановиться на нулевой маске, то алгоритм может войти в бесконечный цикл.

Перебор всех масок с их подмасками. Оценка

Во многих задачах, особенно на динамическое программирование по маскам, требуется перебирать все маски, и для каждой маски - все подмаски:

for (int m=0; m<(1<<n); ++m)

for (int s=m; s; s=(s-1)&m)

... использование s и m ...

Докажем, что внутренний цикл суммарно выполнит итераций.

Доказательство: 1 способ. Рассмотрим -ый бит. Для него, вообще говоря, есть ровно три варианта: он не входит в маску (и потому в подмаску ); он входит в , но не входит в ; он входит в и в . Всего битов , поэтому всего различных комбинаций будет , что и требовалось доказать.

Доказательство: 2 способ. Заметим, что если маска имеет включённых битов, то она будет иметь

Посчитаем эту сумму. Для этого заметим, что она есть не что иное, как разложение в бином Ньютона выражения , т.е. , что и требовалось доказать.

Первообразные корни

Определение

В частности, для случая простого степени первообразного корня пробегают по всем числам от до .

Существование

Первообразный корень по модулю существует тогда и только тогда, когда является либо степенью нечётного простого, либо удвоенной степенью простого, а также в случаях , , .

Эта теорема (которая была полностью доказана Гауссом в 1801 г.) приводится здесь без доказательства.

Связь с функцией Эйлера

Пусть - первообразный корень по модулю . Тогда можно показать, что наименьшее число , для

которого (т.е. — показатель (multiplicative order)), равно . Более того, верно и обратное, и этот факт будет использован нами ниже в алгоритме нахождения первообразного корня.

Алгоритм нахождения первообразного корня

Наивный алгоритм потребует для каждого тестируемого значения времени, чтобы вычислить все его степени

и проверить, что они все различны. Это слишком медленный алгоритм, ниже мы с помощью нескольких известных теорем из теории чисел получим более быстрый алгоритм.

. Это уже значительно более быстрый алгоритм, однако можно пойти ещё дальше.

т.е. всё равно среди чисел вида нашлось бы то, для которого условие не выполнилось, что и требовалось доказать.

все эти числа оказались отличными от , то это и является искомым первообразным корнем.

Время работы алгоритма (считая, что у числа имеется делителей, а возведение в

Про скорость роста первообразных корней с ростом известны лишь приблизительные оценки. Известно,

что первообразные корни — сравнительно небольшие величины. Одна из известных оценок — оценка Шупа (Shoup), что, в предположении истинности гипотезы Римана, первообразный корень есть .

Реализация

Функция powmod() выполняет бинарное возведение в степень по модулю, а функция generator (int p) -

добавить вычисление функции Эйлера в переменной phi.

int powmod (int a, int b, int p) { int res = 1;

while (b)

if (b & 1)

res = int (res * 1ll * a % p), --b;

else

a = int (a * 1ll * a % p), b >>= 1;

return res;

}

int generator (int p) { vector<int> fact;

int phi = p-1, n = phi; for (int i=2; i*i<=n; ++i)

if (n % i == 0) { fact.push_back (i); while (n % i == 0)

n /= i;

}

if (n > 1)

fact.push_back (n);

for (int res=2; res<=p; ++res) { bool ok = true;

for (size_t i=0; i<fact.size() && ok; ++i)

ok &= powmod (res, phi / fact[i], p) != 1; if (ok) return res;

}

return -1;

}