e-maxx_algo

Мне не известна более-менее хорошая асимптотическая оценка этого алгоритма. Я встречал только оценку O (N M)

у похожего алгоритма.

Однако на практике алгоритма зарекомендовал себя очень хорошо: время его работы я оцениваю как O (M log N), хотя, повторюсь, это исключительно экспериментальная оценка.

Реализация

typedef pair<int,int> rib;

typedef vector < vector<rib> > graph;

const int inf = 1000*1000*1000;

int main()

{

int n, v1, v2; graph g (n);

... чтение графа ...

vector<int> d (n, inf); d[v1] = 0;

vector<int> id (n); deque<int> q; q.push_back (v1); vector<int> p (n, -1);

while (!q.empty())

{

int v = q.front(), q.pop_front(); id[v] = 1;

for (size_t i=0; i<g[v].size(); ++i)

{

int to = g[v][i].first, len = g[v][i].second; if (d[to] > d[v] + len)

{

d[to] = d[v] + len; if (id[to] == 0)

q.push_back (to); else if (id[to] == 1)

q.push_front (to); p[to] = v;

id[to] = 1;

}

}

}

... вывод результата ...

}

Алгоритм Флойда-Уоршелла нахождения кратчайших путей между всеми парами вершин

Дан ориентированный или неориентированный взвешенный граф с вершинами. Требуется найти значения всех величин — длины кратчайшего пути из вершины в вершину .

Предполагается, что граф не содержит циклов отрицательного веса (тогда ответа между некоторыми парами вершин может просто не существовать — он будет бесконечно маленьким).

Этот алгоритм был одновременно опубликован в статьях Роберта Флойда (Robert Floyd) и Стивена Уоршелла (Варшалла) (Stephen Warshall) в 1962 г., по имени которых этот алгоритм и называется в настоящее время. Впрочем, в 1959 г. Бернард Рой (Bernard Roy) опубликовал практически такой же алгоритм, но его публикация

осталась незамеченной.

Описание алгоритма

Ключевая идея алгоритма — разбиение процесса поиска кратчайших путей на фазы.

путей, которые содержат в качестве внутренних вершин только вершины из множества (вершины графа мы нумеруем, начиная с единицы).

если этому пути разрешается заходить только в вершины с номерами, меньшими (начало и конец пути не считаются). Легко убедиться, что чтобы это свойство выполнилось для первой фазы, достаточно в матрицу расстояний

если между какими-то вершинами ребра нет, то записать следует величину "бесконечность" . Из вершины в саму себя всегда следует записывать величину , это критично для алгоритма.

В этом случае величина не изменится при переходе с -ой на 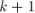-ую фазу.

●"Новый" кратчайший путь стал лучше "старого" пути.

этих половинок была посчитана ещё на -ой фазе или ещё раньше, и нам достаточно взять просто сумму , она и даст длину "нового" кратчайшего пути.

Объединяя эти два случая, получаем, что на -ой фазе требуется пересчитать длины кратчайших путей между всеми парами вершин и следующим образом:

new_d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Таким образом, вся работа, которую требуется произвести на -ой фазе — это перебрать все пары вершин и пересчитать длину кратчайшего пути между ними. В результате после выполнения -ой фазы в матрице

в матрице . В самом деле, если мы улучшили (уменьшили) какое-то значение в матрице расстояний, мы не могли ухудшить тем самым длину кратчайшего пути для каких-то других пар вершин, обработанных позднее.

Асимптотика алгоритма, очевидно, составляет .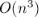

Реализация

for (int k=0; k<n; ++k)

for (int i=0; i<n; ++i)

for (int j=0; j<n; ++j)

d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно.

Правда, если не принять специальных мер, то при наличии в графе рёбер отрицательного веса,

врезультирующей матрице могут появиться числа вида , , и т.д., которые, конечно, попрежнему означают, что между соответствующими вершинами вообще нет пути. Поэтому при наличии в

графе отрицательных рёбер алгоритм Флойда лучше написать так, чтобы он не выполнял переходы из тех состояний,

вкоторых уже стоит "нет пути":

for (int k=0; k<n; ++k)

for (int i=0; i<n; ++i)

for (int j=0; j<n; ++j)

if (d[i][k] < INF && d[k][j] < INF)

d[i][j] = min (d[i][j], d[i][k] + d[k][j]);

Восстановление самих путей

Легко поддерживать дополнительную информацию — так называемых "предков", по которым можно будет восстанавливать сам кратчайший путь между любыми двумя заданными вершинами в

виде последовательности вершин.

Для этого достаточно кроме матрицы расстояний поддерживать также матрицу предков , которая

для каждой пары вершин будет содержать номер фазы, на которой было получено кратчайшее расстояние между ними. Понятно, что этот номер фазы является не чем иным, как "средней" вершиной искомого кратчайшего пути, и теперь нам просто надо найти кратчайший путь между вершинами и , а также между и .

Отсюда получается простой рекурсивный алгоритм восстановления кратчайшего пути.

Случай вещественных весов

Если веса рёбер графа не целочисленные, а вещественные, то следует учитывать погрешности, неизбежно возникающие при работе с типами с плавающей точкой.

Применительно к алгоритму Флойда неприятным спецэффектом этих погрешностей становится то, что найденные алгоритмом расстояния могут уйти сильно в минус из-за накопившихся ошибок. В самом деле, если на первой фазе имела место ошибка , то на второй итерации эта ошибка уже может превратиться в 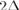, на третьей — в 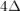, и так далее.

Чтобы этого не происходило, сравнения в алгоритме Флойда следует делать с учётом погрешности:

if (d[i][k] + d[k][j] < d[i][j] - EPS) d[i][j] = d[i][k] + d[k][j];

Случай отрицательных циклов

Если в графе есть циклы отрицательного веса, то формально алгоритм Флойда-Уоршелла неприменим к такому графу. На самом же деле, для тех пар вершин и , между которыми нельзя зайти в цикл отрицательного вес,

алгоритм отработает корректно.

Для тех же пар вершин, ответа для которых не существует (по причине наличия отрицательного цикла на пути между ними), алгоритм Флойда найдёт в качестве ответа какое-то число (возможно, сильно отрицательное, но

не обязательно). Тем не менее, можно улучшить алгоритм Флойда, чтобы он аккуратно обрабатывал такие пары вершин и выводил для них, например, .

Для этого можно сделать, например, следующий критерий "не существования пути". Итак, пусть на данном графе отработал обычный алгоритм Флойда. Тогда между вершинами и не существует кратчайшего пути тогда и только тогда, когда найдётся такая вершина , достижимая из и из которой достижима , для которой выполняется .

Кроме того, при использовании алгоритма Флойда для графов с отрицательными циклами следует помнить, что возникающие в процессе работы расстояния могут сильно уходить в минус, экспоненциально с каждой фазой. Поэтому следует принять меры против целочисленного переполнения, ограничив все расстояния снизу какойнибудь величиной (например, ).

Более подробно об этой задаче см. отдельную статью: "Нахождение отрицательного цикла в графе".

умножается на матрицу , только в операции умножения вместо суммы по всем 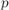берётся минимум по всем :

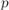где операция умножения двух матриц определяется следующим образом:

Таким образом, решение этой задачи можно представить с помощью этой операции умножения следующим образом:

Осталось заметить, что возведение в степень с этой операцией умножения можно произвести эффективно с помощью алгоритма Бинарного возведения в степень, поскольку единственное требуемое для

него свойство — ассоциативность операции умножения — очевидно, имеется.

Итак, полученное решение имеет асимптотику и заключается в бинарном возведении в -ую степень матрицы смежности графа с изменённой операцией умножения матриц.

Тривиальная реализация: алгоритмы за и

Этот алгоритм можно улучшить, если просматривать каждый раз не все рёбра, а только по одному ребру из каждой уже выбранной вершины. Для этого, например, можно отсортировать рёбра из каждой вершины в порядке возрастания весов, и хранить указатель на первое допустимое ребро (напомним, допустимы только те рёбра, которые ведут в множество ещё не выбранных вершин). Тогда, если пересчитывать эти указатели при каждом

Ниже мы рассмотрим два немного других алгоритма: для плотных и для разреженных графов, получив в итоге заметно лучшую асимптотику.

Случай плотных графов: алгоритм за

Подойдём к вопросу поиска наименьшего ребра с другой стороны: для каждой ещё не выбранной будем хранить минимальное ребро, ведущее в уже выбранную вершину.

Тогда, чтобы на текущем шаге произвести выбор минимального ребра, надо просто просмотреть эти минимальные рёбра у каждой не выбранной ещё вершины — асимптотика составит .

Но теперь при добавлении в остов очередного ребра и вершины эти указатели надо пересчитывать. Заметим, что эти указатели могут только уменьшаться, т.е. у каждой не просмотренной ещё вершины надо либо оставить её указатель без изменения, либо присвоить ему вес ребра в только что добавленную вершину. Следовательно, эту фазу можно сделать также за .

Таким образом, мы получили вариант алгоритма Прима с асимптотикой .

В частности, такая реализация особенно удобна для решения так называемой евклидовой задачи о минимальном остове: когда даны точек на плоскости, расстояние между которыми измеряется

по стандартной евклидовой метрике, и требуется найти остов минимального веса, соединяющий их все (причём добавлять новые вершины где-либо в других местах запрещается). Эта задача решается описанным здесь алгоритмом за времени и памяти, чего не получится добиться алгоритмом Крускала.

Реализация алгоритма Прима для графа, заданного матрицей смежности :

//входные данные int n;

vector < vector<int> > g;

const int INF = 1000000000; // значение "бесконечность"

//алгоритм

vector<bool> used (n);

vector<int> min_e (n, INF), sel_e (n, -1); min_e[0] = 0;

for (int i=0; i<n; ++i) { int v = -1;

for (int j=0; j<n; ++j)

if (!used[j] && (v == -1 || min_e[j] < min_e[v])) v = j;

if (min_e[v] == INF) { cout << "No MST!"; exit(0);

}

used[v] = true;

if (sel_e[v] != -1)

cout << v << " " << sel_e[v] << endl;

for (int to=0; to<n; ++to)

if (g[v][to] < min_e[to]) { min_e[to] = g[v][to]; sel_e[to] = v;

}

}

вывода рёбер в ответе). Алгоритм делает шагов, на каждом из которых выбирает вершину с наименьшей меткой , помечает её , и затем просматривает все рёбра из этой вершины, пересчитывая их метки.

Случай разреженных графов: алгоритм за

В описанном выше алгоритме можно увидеть стандартные операции нахождения минимума в множестве и изменение значений в этом множестве. Эти две операции являются классическими, и выполняются многими структурами данных, например, реализованным в языке C++ красно-чёрным деревом set.

//входные данные int n;

vector < vector < pair<int,int> > > g;

const int INF = 1000000000; // значение "бесконечность"

//алгоритм

vector<int> min_e (n, INF), sel_e (n, -1); min_e[0] = 0;

set < pair<int,int> > q; q.insert (make_pair (0, 0)); for (int i=0; i<n; ++i) {

if (q.empty()) {

cout << "No MST!"; exit(0);

}

int v = q.begin()->second; q.erase (q.begin());

if (sel_e[v] != -1)

cout << v << " " << sel_e[v] << endl;

for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first,

cost = g[v][j].second; if (cost < min_e[to]) {

q.erase (make_pair (min_e[to], to)); min_e[to] = cost;

sel_e[to] = v;

q.insert (make_pair (min_e[to], to));

}

}

}

(это нужно для вывода рёбер в ответе). Кроме того, поддерживается очередь из всех вершин в порядке увеличения их меток . Алгоритм делает шагов, на каждом из которых выбирает вершину с наименьшей меткой

(просто извлекая её из начала очереди), и затем просматривает все рёбра из этой вершины, пересчитывая их метки (при пересчёте мы удаляем из очереди старую величину, и затем кладём обратно новую).

Аналогия с алгоритмом Дейкстры

В двух описанных только что алгоритмах прослеживается вполне чёткая аналогия с алгоритмом Дейкстры: он имеет

такую же структуру ( фаза, на каждой из которых сначала выбирается оптимальное ребро, добавляется в ответ, а затем пересчитываются значения для всех не выбранных ещё вершин). Более того, алгоритм Дейкстры тоже имеет