e-maxx_algo

то только в одну сторону: может сообщить об отсутствии совершенного паросочетания, когда на самом деле оно существует.

Мы можем повторить этот тест несколько раз, подставляя в качестве значений переменных новые случайные числа, и с каждым повторным запуском мы получаем всё большую уверенность в том, что тест выдал правильный ответ.

На практике в большинстве случаев достаточно одного теста, чтобы определить, есть ли в графе совершенное паросочетание или нет; несколько таких тестов дают уже весьма высокую вероятность.

Для оценки вероятности ошибки можно использовать лемму Шварца-Зиппеля (Schwartz–Zippel), которая гласит, что вероятность обращения в ноль ненулевого полинома -ой степени при подстановке в качестве значений переменных случайных чисел, каждое из которых может принимать вариантов значения, — эта вероятность удовлетворяет неравенству:

на количество итераций теста. Стоит отметить, что по асимптотике такое решение значительно отстаёт от решения алгоритмом Эдмондса сжатия цветков, однако в некоторых случаях более предпочтительно из-за

простоты реализации.

Восстановить само совершенное паросочетание как набор рёбер является более сложной задачей. Самым простым, хотя и медленным, вариантом будет восстановление этого паросочетания по одному ребру: перебираем первое ребро ответа, выбираем его так, чтобы в оставшемся графе существовало совершенное паросочетание, и т.д.

Доказательство теоремы Татта

Чтобы хорошо понять доказательство этой теоремы, сначала рассмотрим более простой результат, — полученный Эдмондсом для случая двудольных графов.

Теорема Эдмондса

Рассмотрим двудольный граф, в каждой доле которого по вершин. Составим матрицу , в которой, по аналогии с матрицей Татта, является отдельной независимой переменной, если ребро присутствует в графе,

и является тождественным нулём в противном случае.

Эта матрица похожа на матрицу Татта, однако матрица Эдмондса имеет вдвое меньшую разность, и каждому ребру здесь соответствует только одна ячейка матрицы.

двудольном графе существует совершенное паросочетание.

Доказательство. Распишем определитель согласно его определению, как сумма по всем перестановкам:

Заметим, что поскольку все ненулевые элементы матрицы — различные независимые переменные, то в этой сумме все ненулевые слагаемые различны, а потому никаких сокращений в процессе суммирования не происходит. Осталось заметить, что любое ненулевое слагаемое в этой сумме означает непересекающийся по вершинам набор рёбер, т.е. некоторое совершенное паросочетание. И наоборот, любому совершенному паросочетанию соответствует ненулевое слагаемое в этой сумме. Вкупе с вышесказанным это доказывает теорему.

Свойства антисимметричных матриц

Для доказательства теоремы Татта необходимо воспользоваться несколькими известными фактами линейной алгебры о свойствах антисимметричных матриц.

Во-первых (этот факт нам не пригодится, но он интересен сам по себе), если антисимметричная матрица имеет нечётный размер, то её определитель всегда равен нулю (теорема Якоби (Jacobi)). Для этого достаточно

заметить, что антисимметричная матрица удовлетворяет равенству 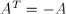, и теперь получаем цепочку равенств:

откуда и следует, что при нечётных определитель необходимо должен быть равен нулю.

Во-вторых, оказывается, что в случае антисимметричных матриц чётного размера их определитель всегда можно записать как квадрат некоторого полинома относительно переменных-элементов этой матрицы (полином называется пфаффианом (pfaffian), а результат принадлежит Мьюру (Muir)):

В-третьих, этот пфаффиан представляет собой не произвольный многочлен, а сумму вида:

Доказательство теоремы Татта

Воспользовавшись вторым и третьим свойством из предыдущего пункта, мы получаем, что определитель матрицы Татта представляет собой квадрат от суммы слагаемых такого вида, что каждое слагаемое

— произведение элементов матрицы, индексы которых не повторяются и покрывают все номера от до . Таким образом, снова, как и в доказательстве теоремы Эдмондса, каждое ненулевое слагаемое этой суммы соответствует совершенному паросочетанию в графе, и наоборот.

Теорема Ловаса: обобщение для поиска размера максимального паросочетания

Формулировка

Ранг матрицы Татта совпадает с удвоенной величиной максимального паросочетания в данном графе.

Применение

Для применения этой теоремы на практике можно воспользоваться тем же самым приёмом рандомизации, что и в вышеописанном алгоритме для матрицы Татта, а именно: подставить вместо переменных случайные значения, и найти ранг полученной числовой матрицы. Ранг матрицы, опять же, ищется за с помощью

модифицированного алгоритма Гаусса, см. здесь.

Впрочем, следует отметить, что приведённая в предыдущем алгоритме лемма Шварца-Зиппеля неприменима в явном виде, и интуитивно кажется, что вероятность ошибки здесь становится выше. Однако утверждается (см. работы Ловаса (Lovasz)), что и здесь вероятность ошибки (т.е. того, что ранг полученной матрицы окажется меньше, чем удвоенный размер максимального паросочетания) не превосходит (где , как и выше, обозначает

размер множества, из которого выбираются случайные числа).

Доказательство

Доказательство будет вытекать из одного свойства, известного из линейной алгебры. Пусть дана

только строками с номерами из и столбцами с номерами из . Тогда выполняется:

Покажем, как это свойство позволяет установить соответствие между рангом матрицы Татта и величиной максимального паросочетания.

С одной стороны, рассмотрим в графе некоторое максимальное паросочетание, и обозначим множество насыщаемых им вершин через . Тогда определитель отличен от нуля (по теореме Татта).

Следователь, ранг матрицы Татта как минимум не меньше удвоенной величины максимального паросочетания.

и завершает доказательство теоремы.

Алгоритм Рабина-Вазирани нахождения максимального паросочетания

Этот алгоритм является дальнейшим обобщением двух предыдущих теорем, и позволяет, в отличие от них, выдавать не только величину максимального паросочетания, но и сами рёбра, входящие в него.

Формулировка теоремы

Пусть в графе существует совершенное паросочетание. Тогда его матрица Татта невырождена, т.е.

. Сгенерируем по ней, как было описано выше, случайную числовую матрицу . Тогда, с

нуля, поэтому обратная матрица существует.)

Применение

Эту теорему можно применять для восстановления самих рёбер максимального паросочетания. Сначала придётся выделить подграф, в котором содержится искомое максимальное паросочетание (это можно сделать параллельно с алгоритмом поиска ранга матрицы).

После этого задача сводится к поиску совершенного паросочетания по данной числовой матрице, полученной из матрицы Татта. Здесь мы уже применяем теорему Рабина-Вазирани, — находим обратную матрицу (что можно

получаем простоту решения (по сравнению, например, с алгоритмом Эдмондса сжатия цветков).

Доказательство теоремы

Вспомним известную формулу для элементов обратной матрицы :

определитель матрицы, получаемой из удалением -й строки и -го столбца.

-ой строкой и -ым столбцом имеет ненулевой определитель, что, применяя теорему Татта, означает с высокой вероятностью, что в графе без вершин и по-прежнему существует совершенное паросочетание.

Литература

●William Thomas Tutte. The Factorization of Linear Graphs [1946]

●Laszlo Lovasz. On Determinants, Matchings and Random Algorithms [1979]

●Laszlo Lovasz, M.D. Plummer. Matching Theory [1986]

●Michael Oser Rabin, Vijay V. Vazirani. Maximum matchings in general graphs through randomization [1989]

●Allen B. Tucker. Computer Science Handbook [2004]

●Rajeev Motwani, Prabhakar Raghavan. Randomized Algorithms [1995]

●A.C. Aitken. Determinants and matrices [1944]

Рёберная связность. Свойства и нахождение

Определение

Ясно, что рёберная связность графа равна минимуму от наименьшего числа рёбер, разделяющих две вершины и , взятому среди всевозможных пар .

Свойства

Соотношение Уитни

Соотношение Уитни (Whitney) (1932 г.) между рёберной связностью , вершинной связностью и наименьшей из степеней вершин :

Докажем это утверждение.

мы возьмём от каждого из этих ребёр по одному концу (любому из двух) и удалим из графа, то тем самым с помощью удалённых вершин (поскольку одна и та же вершина могла встретиться дважды) мы сделаем граф несвязным.

Таким образом, .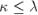

Докажем второе неравенство: . Рассмотрим вершину минимальной степени, тогда мы можем удалить все

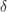смежных с ней рёбер и тем самым отделить эту вершину от всего остального графа. Следовательно, .

Интересно, что неравенство Уитни нельзя улучшить: т.е. для любых троек чисел, удовлетворяющих этому неравенству, существует хотя бы один соответствующий граф. См. задачу "Построение графа с

указанными величинами вершинной и рёберной связностей и наименьшей из степеней вершин".

Теорема Форда-Фалкерсона

Теорема Форда-Фалкерсона (1956 г.):

Для любых двух вершин наибольшее число рёберно-непересекающихся цепей, соединяющих их, равно наименьшему числу рёбер, разделяющих эти вершины.

Нахождение рёберной связности

Простой алгоритм на основе поиска максимального потока

Этот способ основан на теореме Форда-Фалекрсона.

Мы должны перебрать все пары вершин , и между каждой парой найти наибольшее число непересекающихся

по рёбрам путей. Эту величину можно найти с помощью алгоритма максимального потока: мы делаем истоком,

— стоком, а пропускную способность каждого ребра кладём равной 1. Таким образом, псевдокод алгоритма таков:

int ans = INF;

for (int s=0; s<n; ++s)

for (int t=s+1; t<n; ++t) {

int flow = ... величина максимального потока из s в t ...

ans = min (ans, flow);

}

Асимптотика алгоритма при использовании \edmonds_karp{алгоритма Эдмондса-Карпа нахождения максимального потока} получается , однако следует заметить, что скрытая в асимптотике

константа весьма мала, поскольку практически невозможно создать такой граф, чтобы алгоритм нахождения максимального потока работал медленно сразу при всех стоках и истоках.

Особенно быстро такой алгоритм будет работать на случайных графах.

Специальный алгоритм

Используя потоковую терминологию, данная задача — это задача поиска глобального минимального разреза.

Для её решения разработаны специальные алгоритмы. На данном сайте представлен один из которых — алгоритм Штор-Вагнера, работающий за время или .

Литература

●Hassler Whitney. Congruent Graphs and the Connectivity of Graphs [1932]

●Фрэнк Харари. Теория графов [2003]

Рёберная связность. Свойства и нахождение

Определение

Пусть дан неориентированный граф с вершинами и рёбрами.

Вершинной связностью графа называется наименьшее число вершин, которое нужно удалить, чтобы граф перестал быть связным.

Например, для несвязного графа вершинная связность равна нулю. Для связного графа с единственной точкой сочленения вершинная связность равна единице. Для полного графа вершинную связность полагают равной (поскольку, какую пару вершин мы ни выберем, даже удаление всех остальных вершин не сделает их несвязными). Для всех графов, кроме полного, вершинная связность не превосходит — поскольку можно найти пару вершин, между которыми нет ребра, и удалить все остальные вершины.

Говорят, что множество вершин разделяет вершины и , если при удалении этих вершин из графа вершины и оказываются в разных компонентах связности.

Ясно, что вершинная связность графа равна минимуму от наименьшего числа вершин, разделяющих две вершины и , взятому среди всевозможных пар .

Свойства

Соотношение Уитни

Соотношение Уитни (Whitney) (1932 г.) между рёберной связностью , вершинной связностью и наименьшей из степеней вершин :

Докажем это утверждение.

мы возьмём от каждого из этих ребёр по одному концу (любому из двух) и удалим из графа, то тем самым с помощью удалённых вершин (поскольку одна и та же вершина могла встретиться дважды) мы сделаем граф несвязным.

Таким образом, .

Докажем второе неравенство: . Рассмотрим вершину минимальной степени, тогда мы можем удалить все

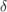смежных с ней рёбер и тем самым отделить эту вершину от всего остального графа. Следовательно, .

Интересно, что неравенство Уитни нельзя улучшить: т.е. для любых троек чисел, удовлетворяющих этому неравенству, существует хотя бы один соответствующий граф. См. задачу "Построение графа с

указанными величинами вершинной и рёберной связностей и наименьшей из степеней вершин".

Нахождение вершинной связности

Переберём пару вершин и , и найдём минимальное количество вершин, которое надо удалить, чтобы разделить и .

Для этого раздвоим каждую вершину: т.е. у каждой вершины создадим по две копии — одна для входящих рёбер, другая — для выходящих, и эти две копии связаны друг с другом ребром .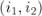

Каждое ребро 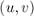исходного графа в этой модифицированной сети превратится в два ребра: и .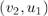

Всем рёбрам проставим пропускную способность, равную единице. Найдём теперь максимальный поток в этом графе между истоком и стоком . По построению графа, он и будет являться минимальным количеством вершин, необходимых для разделения и .

Таким образом, если для поиска максимального потока мы выберем алгоритм Эдмондса-Карпа, работающий за

асимптотике, весьма мала: поскольку сделать граф, на котором алгоритмы бы работали долго при любой паре истоксток, практически невозможно.

Построение графа с указанными величинами вершинной и рёберной связностей и наименьшей из степеней вершин

Даны величины , , — это, соответственно, вершинная связность, рёберная связность и наименьшая из

степеней вершин графа. Требуется построить граф, который бы обладал указанными значениями, или сказать, что такого графа не существует.

Соотношение Уитни

Соотношение Уитни (Whitney) (1932 г.) между рёберной связностью , вершинной связностью и наименьшей из степеней вершин :

Докажем это утверждение.

мы возьмём от каждого из этих ребёр по одному концу (любому из двух) и удалим из графа, то тем самым с помощью удалённых вершин (поскольку одна и та же вершина могла встретиться дважды) мы сделаем граф несвязным.

Таким образом, .

Докажем второе неравенство: . Рассмотрим вершину минимальной степени, тогда мы можем удалить все

смежных с ней рёбер и тем самым отделить эту вершину от всего остального графа. Следовательно, .

Интересно, что неравенство Уитни нельзя улучшить: т.е. для любых троек чисел, удовлетворяющих этому неравенству, существует хотя бы один соответствующий граф. Это мы докажем конструктивно, показав, как строятся соответствующие графы.

Решение

Проверим, удовлетворяют ли данные числа , и соотношению Уитни. Если нет, то ответа не существует.

того, соединим эти две части рёбрами так, чтобы в первой части эти рёбра были смежны вершинам, а в другой части — вершинам. Легко убедиться в том, что полученный граф будет обладать необходимыми характеристиками.

Обратная задача SSSP (inverse-SSSP -

обратная задача кратчайших путей из одной вершины)

Имеется взвешенный неориентированный мультиграф G из N вершин и M рёбер. Дан массив P[1..N] и указана некоторая начальная вершина S. Требуется изменить веса рёбер так, чтобы для всех I P[I] было равно длине кратчайшего пути из S в I, причём сумма всех изменений (сумма модулей изменений весов рёбер) была бы наименьшей. Если этого сделать невозможно, то алгоритм должен выдать "No solution". Делать вес ребра отрицательным запрещено.

Описание решения

Мы решим эту задачу за линейное время, просто перебрав все рёбра (т.е. за один проход).

Пусть на текущем шаге мы рассматриваем ребро из вершины A в вершину B длиной R. Мы предполагаем, что для вершины A уже все условия выполнены (т.е. расстояние от S до A действительно равно P[A]), и будем проверять выполнение условий для вершины B. Имеем несколько вариантов ситуации:

●1. P[A] + R < P[B]

Это означает, что мы нашли путь, более короткий, чем он должен быть. Поскольку P[A] и P[B] мы изменять не можем, то мы обязаны удлинить текущее ребро (независимо от остальных рёбер), а именно выполнить:

R += P[B] - P[A] - R.

Кроме того, это означает, что мы нашли уже путь в вершину B из S, длина которого равна требуемому значению P [B], поэтому на последующих шагах нам не придётся укорачивать какие-либо рёбра (см. вариант 2).

●2. P[A] + R >= P[B]

Это означает, что мы нашли путь, более длинный, чем требуемый. Поскольку таких путей может быть несколько,

мы должны выбрать среди всех таких путей (рёбер) то, которое потребует наименьшего изменения. Повторимся, что если мы удлиняли какое-то ребро, ведущее в вершину B (вариант 1), то этим мы фактически построили кратчайший путь в вершину B, а потому укорачивать никакое ребро уже не надо будет. Таким образом, для каждой вершины мы

должны хранить ребро, которое собираемся укорачивать, т.е. ребро с наименьшим весом изменения.

Таким образом, просто перебрав все рёбра, и рассмотрев для каждого ребра ситуацию (за O(1)), мы решим обратную задачу SSSP за линейное время.

Если в какой-то момент мы пытаемся изменить уже изменённое ребро, то, очевидно, этого делать нельзя, и следует выдать "No solution". Кроме того, у некоторых вершин может быть так и не достигнута требуемая оценка кратчайшего пути, тогда ответ тоже будет "No solution". Во всех остальных случаях (кроме, конечно, явно некорректных значений в массиве P, т.е. P[S] != 0 или отрицательные значения) ответ будет существовать.

Реализация

Программа выводит "No solution", если решения нет, иначе выводит в первой строке минимальную сумму изменений весов рёбер, а в последующих M строках - новые веса рёбер.

const int INF = 1000*1000*1000; int n, m;

vector<int> p (n);

bool ok = true;

vector<int> cost (m), cost_ch (m), decrease (n, INF), decrease_id (n, -1); decrease[0] = 0;

for (int i=0; i<m; ++i) {

int a, b, c; // текущее ребро (a,b) с ценой c cost[i] = c;

for (int j=0; j<=1; ++j) {

int diff = p[b] - p[a] - c; if (diff > 0) {

ok &= cost_ch[i] == 0 || cost_ch[i] == diff; cost_ch[i] = diff;

decrease[b] = 0;

}

else

if (-diff <= c && -diff < decrease[b]) { decrease[b] = -diff; decrease_id[b] = i;

}

swap (a, b);

}

}

for (int i=0; i<n; ++i) {

ok &= decrease[i] != INF; int r_id = decrease_id[i]; if (r_id != -1) {

ok &= cost_ch[r_id] == 0 || cost_ch[r_id] == -decrease[i]; cost_ch[r_id] = -decrease[i];

}

}

if (!ok)

cout << "No solution";

else {

long long sum = 0;

for (int i=0; i<m; ++i) sum += abs (cost_ch[i]); cout << sum << '\n';

for (int i=0; i<m; ++i)

printf ("%d ", cost[i] + cost_ch[i]);

}

Обратная задача MST (inverse-MST -

обратная задача минимального остова) за O (N M2)

Дан взвешенный неориентированный граф G с N вершинами и M рёбрами (без петель и кратных рёбер). Известно, что граф связный. Также указан некоторый остов T этого графа (т.е. выбрано N-1 ребро, которые образуют дерево с N вершинами). Требуется изменить веса рёбер таким образом, чтобы указанный остов T являлся минимальным остовом этого графа (точнее говоря, одним из минимальных остовов), причём сделать это так, чтобы суммарное изменение всех весов было наименьшим.

Решение

Сведём задачу inverse-MST к задаче min-cost-flow, точнее, к задаче, двойственной min-cost-flow

(в смысле двойственности задач линейного программирования); затем решим последнюю задачу.

Итак, пусть дан граф G с N вершинами, M рёбрами. Вес каждого ребра обозначим через Ci. Предположим, не теряя общности, что рёбра с номерами с 1 по N-1 являются рёбрами T.

1. Необходимое и достаточное условие MST

Пусть дан некоторый остов S (не обязательно минимальный).

Введём сначала одно обозначение. Рассмотрим некоторое ребро j, не принадлежащее S. Очевидно, в графе S имеется единственный путь, соединяющий концы этого ребра, т.е. единственный путь, соединяющий концы ребра j и состоящий только из рёбер, принадлежащих S. Обозначим через P[j] множество рёбер, образующих этот путь для j-го ребра.

Для того, чтобы некоторый остов S являлся минимальным, необходимо и достаточно, чтобы:

Ci <= Cj для всех j S и каждого i P[j]

Можно заметить, что, поскольку в нашей задаче остову T принадлежат рёбра 1..N-1, то мы можем записать это условие таким образом:

Ci <= Cj для всех j = N..M и каждого i P[j] (причём все i лежат в диапазоне 1..N-1)

2. Граф путей

Понятие графа путей непосредственно связано с предыдущей теоремой. Пусть дан некоторый остов S (не обязательно минимальный).

Тогда графом путей H для графа G будет следующий граф:

●Он содержит M вершин, каждая вершина в H взаимно однозначно соответствует некоторому ребру в G.

●Граф H двудольный. В первой его доле находятся вершины i, которые соответствуют рёбрам в G, принадлежащим остову S. Соответственно, во второй доле находятся вершины j, которые соответствуют рёбрам, не принадлежащим S.

●Ребро проводится из вершины i в вершину j тогда и только тогда, когда i принадлежит P[j].

Иными словами, для каждой вершины j из второй доли в неё входят рёбра из всех вершин первой доли, соответствующих множеству рёбер P[j].

Вслучае нашей задачи мы можем немного упростить описание графа путей:

ребро (i,j) существует в H, если i P[j], j = N..M, i = 1..N-1

3. Математическая формулировка задачи

Чисто формально задача inverse-MST записывается таким образом:

найти массив A[1..M] такой, что

Ci + Ai <= Cj + Aj для всех j = N..M и каждого i P[j] (i в 1..N-1),

и минимизировать сумму |A1| + |A2| + ... + |Am|