e-maxx_algo

Нахождение кратчайших путей от заданной вершины до всех остальных вершин алгоритмом Дейкстры

Постановка задачи

Дан ориентированный или неориентированный взвешенный граф с вершинами и рёбрами. Веса всех рёбер неотрицательны. Указана некоторая стартовая вершина . Требуется найти длины кратчайших путей из вершины во все остальные вершины, а также предоставить способ вывода самих кратчайших путей.

Эта задача называется "задачей о кратчайших путях с единственным источником" (single-source shortest paths problem).

Алгоритм

Здесь описывается алгоритм, который предложил датский исследователь Дейкстра (Dijkstra) в 1959 г.

компьютере обычно в качестве бесконечности выбирают просто достаточно большое число, заведомо большее возможной длины пути):

Кроме того, для каждой вершины будем хранить, помечена она ещё или нет, т.е. заведём булевский массив

. Изначально все вершины не помечены, т.е.

Сам алгоритм Дейкстры состоит из итераций. На очередной итерации выбирается вершина с наименьшей величиной 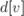среди ещё не помеченных, т.е.:

виде кода релаксация выглядит как:

На этом текущая итерация заканчивается, алгоритм переходит к следующей итерации (снова выбирается вершина с наименьшей величиной , из неё производятся релаксации, и т.д.). При этом в конце концов, после итераций, все вершины графа станут помеченными, и алгоритм свою работу завершает. Утверждается, что найденные значения 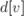и есть искомые длины кратчайших путей из в .

останутся бесконечными. Понятно, что несколько последних итераций алгоритма будут как раз выбирать эти вершины, но никакой полезной работы производить эти итерации не будут (поскольку бесконечное расстояние не сможет прорелаксировать другие, даже тоже бесконечные расстояния). Поэтому алгоритм можно сразу останавливать, как только в качестве выбранной вершины берётся вершина с бесконечным расстоянием.

Восстановление путей. Разумеется, обычно нужно знать не только длины кратчайших путей, но и получить сами пути. Покажем, как сохранить информацию, достаточную для последующего восстановления кратчайшего пути из

можно будет восстановить по нему, просто каждый раз беря предка от текущей вершины, пока мы не придём в стартовую вершину — так мы получим искомый кратчайший путь, но записанный в обратном порядке. Итак,

const int INF = 1000000000;

int main() { int n;

... чтение n ...

vector < vector < pair<int,int> > > g (n);

... чтение графа ...

int s = ...; // стартовая вершина

vector<int> d (n, INF), p (n); d[s] = 0;

vector<char> u (n);

for (int i=0; i<n; ++i) { int v = -1;

for (int j=0; j<n; ++j)

if (!u[j] && (v == -1 || d[j] < d[v])) v = j;

if (d[v] == INF)

break; u[v] = true;

for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first,

len = g[v][j].second; if (d[v] + len < d[to]) {

d[to] = d[v] + len; p[to] = v;

}

}

}

}

Если расстояние до выбранной вершины оказывается равным бесконечности, то алгоритм останавливается. Иначе вершина помечается как помеченная, и просматриваются все рёбра, исходящие из данной вершины, и

— предки всех вершин (кроме стартовой ). Восстановить путь до любой вершины можно следующим образом:

vector<int> path;

for (int v=t; v!=s; v=p[v]) path.push_back (v);

path.push_back (s);

reverse (path.begin(), path.end());

Литература

●Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: Построение и анализ [2005]

●Edsger Dijkstra. A note on two problems in connexion with graphs [1959]

Нахождение кратчайших путей от заданной вершины до всех остальных вершин алгоритмом Дейкстры для разреженных графов

Постановку задачи, алгоритм и его доказательство см. в статье об общем алгоритме Дейкстры.

Алгоритм

Напомним, что сложность алгоритма Дейкстры складывается из двух основных операций: время нахождения вершины с наименьшей величиной расстояния , и время совершения релаксации, т.е. время изменения величины .

эта оценка, и по вине первого слагаемого. Таким образом, надо улучшать время выполнения операций первого типа, не сильно ухудшая при этом время выполнения операций второго типа.

кратчайшего пути. Кстати говоря, эта оценка является оптимальной для алгоритмов, основанных на алгоритме Дейкстры, т.е. Фибоначчиевы кучи являются оптимальными с этой точки зрения (это утверждение об оптимальности на самом деле основано на невозможности существования такой "идеальной" структуры данных — если бы она существовала, то можно было бы выполнять сортировку за линейное время, что, как известно, в общем случае невозможно;

впрочем, интересно, что существует алгоритм Торупа (Thorup), который ищет кратчайший путь с оптимальной, линейной, асимптотикой, но основан он на совсем другой идее, чем алгоритм Дейкстры, поэтому никакого противоречия здесь нет). Однако, Фибоначчиевы кучи довольно сложны в реализации (и, надо отметить, имеют немалую константу, скрытую в асимптотике).

В качестве компромисса можно использовать структуры данных, позволяющие выполнять оба типа

не меняет, но скрытую константу увеличивает).

Реализация

set

то удобно в контейнер помещать пары: первый элемент пары — расстояние, а второй — номер вершины. В результате

в будут храниться пары, автоматически упорядоченные по расстояниям, что нам и нужно. const int INF = 1000000000;

int main() { int n;

... чтение n ...

vector < vector < pair<int,int> > > g (n);

... чтение графа ...

int s = ...; // стартовая вершина

vector<int> d (n, INF), p (n); d[s] = 0;

set < pair<int,int> > q; q.insert (make_pair (d[s], s)); while (!q.empty()) {

int v = q.begin()->second; q.erase (q.begin());

for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first,

len = g[v][j].second; if (d[v] + len < d[to]) {

q.erase (make_pair (d[to], to)); d[to] = d[v] + len;

p[to] = v;

q.insert (make_pair (d[to], to));

}

}

}

}

нахождения вершины с наименьшим расстоянием, выполняет . Изначально в него помещаем стартовую вершину с её расстоянием. Основной цикл алгоритма выполняется, пока в очереди есть хоть одна вершина. Из очереди извлекается вершина с наименьшим расстоянием, и затем из неё выполняются релаксации. Перед выполнением каждой успешной релаксации мы сначала удаляем из старую пару, а затем, после выполнения релаксации, добавляем обратно новую пару (с новым расстоянием ).

priority_queue

Принципиально здесь отличий от нет, за исключением того момента, что удалять из произвольные элементы невозможно (хотя теоретически кучи поддерживают такую операцию,

в стандартной библиотеке она не реализована). Поэтому приходится совершать "обходной манёвр": при релаксации просто не будем удалять старые пары из очереди. В результате в очереди могут находиться одновременно несколько пар для одной и той же вершины (но с разными расстояниями). Среди этих пар нас интересует только одна, для которой элемент равен , а все остальные являются фиктивными. Поэтому

надо сделать небольшую модификацию: в начале каждой итерации, когда мы извлекаем из очереди очередную пару, будем проверять, фиктивная она или нет (для этого достаточно сравнить и ). Следует отметить, что

это важная модификация: если не сделать её, то это приведёт к значительному ухудшению асимптотики (до ).

Ещё нужно помнить о том, что упорядочивает элементы по убыванию, а не по возрастанию,

как обычно. Проще всего преодолеть эту особенность не указанием своего оператора сравнения, а просто помещая в качестве элементов расстояния со знаком минус. В результате в корне кучи будут оказываться элементы

снаименьшим расстоянием, что нам и нужно. const int INF = 1000000000;

int main() { int n;

... чтение n ...

vector < vector < pair<int,int> > > g (n);

... чтение графа ...

int s = ...; // стартовая вершина

vector<int> d (n, INF), p (n); d[s] = 0;

priority_queue < pair<int,int> > q; q.push (make_pair (0, s));

while (!q.empty()) {

int v = q.top().second, cur_d = -q.top().first; q.pop();

if (cur_d > d[v]) continue;

for (size_t j=0; j<g[v].size(); ++j) { int to = g[v][j].first,

len = g[v][j].second; if (d[v] + len < d[to]) {

d[to] = d[v] + len; p[to] = v;

q.push (make_pair (-d[to], to));

}

}

}

}

Как правило, на практике версия с оказывается несколько быстрее версии с .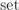

Избавление от pair

Можно ещё немного улучшить производительность, если в контейнерах всё же хранить не пары, а только номера вершин. При этом, понятно, надо перегрузить оператор сравнения для вершин: сравнивать две вершины надо по расстояниям до них .

Поскольку в результате релаксации величина расстояния до какой-то вершины меняется, то надо понимать, что "сама по себе" структура данных не перестроится. Поэтому, хотя может показаться, что удалять/добавлять элементы в контейнер в процессе релаксации не надо, это приведёт к разрушению структуры данных. По-прежнему перед релаксацией надо удалить из структуры данных вершину , а после релаксации вставить её обратно — тогда никакие соотношения между элементами структуры данных не нарушатся.

применим только к . На практике он заметно увеличивает производительность, особенно когда для хранения расстояний используются большие типы данных (как или ).

Алгоритм Форда-Беллмана

Пусть дан ориентированный взвешенный граф с вершинами и рёбрами, и указана некоторая вершина

. Требуется найти длины кратчайших путей от вершины до всех остальных вершин.

В отличие от алгоритма Дейкстры, этот алгоритм применим также и к графам, содержащим рёбра отрицательного

веса. Впрочем, если граф содержит отрицательный цикл, то, понятно, кратчайшего пути до некоторых вершин может не существовать (по причине того, что вес кратчайшего пути должен быть равен минус бесконечности); впрочем, этот алгоритм можно модифицировать, чтобы он сигнализировал о наличии цикла отрицательного веса, или даже выводил сам этот цикл.

Алгоритм носит имя двух американских учёных: Ричарда Беллмана (Richard Bellman) и Лестера Форда (Lester Ford). Форд фактически изобрёл этот алгоритм в 1956 г. при изучении другой математической задачи, подзадача которой свелась к поиску кратчайшего пути в графе, и Форд дал набросок решающего эту задачу алгоритма. Беллман в 1958 г. опубликовал статью, посвящённую конкретно задаче нахождения кратчайшего пути, и в этой статье он чётко сформулировал алгоритм в том виде, в котором он известен нам сейчас.

Описание алгоритма

Мы считаем, что граф не содержит цикла отрицательного веса. Случай наличия отрицательного цикла будет рассмотрен ниже в отдельном разделе.

Сам алгоритм Форда-Беллмана представляет из себя несколько фаз. На каждой фазе просматриваются все рёбра

Утверждается, что достаточно фазы алгоритма, чтобы корректно посчитать длины всех кратчайших путей в графе (повторимся, мы считаем, что циклы отрицательного веса отсутствуют). Для недостижимых вершин расстояние останется равным бесконечности .

Реализация

Для алгоритма Форда-Беллмана, в отличие от многих других графовых алгоритмов, более удобно представлять граф

, список рёбер, и номер стартовой вершины . Все номера вершин нумеруются с по .

Простейшая реализация

Константа обозначает число "бесконечность" — её надо подобрать таким образом, чтобы она заведомо превосходила все возможные длины путей.

struct edge {

int a, b, cost;

};

int n, m, v; vector<edge> e;

const int INF = 1000000000;

void solve() {

vector<int> d (n, INF); d[v] = 0;

for (int i=0; i<n-1; ++i)

for (int j=0; j<m; ++j)

if (d[e[j].a] < INF)

d[e[j].b] = min (d[e[j].b], d[e[j].a] + e

[j].cost);

// вывод d, например, на экран

}

Проверка "if (d[e[j].a] < INF)" нужна, только если граф содержит рёбра отрицательного веса: без такой проверки

бы происходили релаксации из вершин, до которых пути ещё не нашли, и появлялись бы некорректные расстояния вида , , и т.д.

Улучшенная реализация

Этот алгоритм можно несколько ускорить: зачастую ответ находится уже за несколько фаз, а оставшиеся фазы никакой полезной работы не происходит, лишь впустую просматриваются все рёбра. Поэтому будем хранить флаг того, изменилось что-то на текущей фазе или нет, и если на какой-то фазе ничего не произошло, то алгоритм можно останавливать. (Эта оптимизация не улучшает асимптотику, т.е. на некоторых графах по-прежнему будут нужны все фаза, но значительно ускоряет поведение алгоритма "в среднем", т.е. на случайных графах.)

С такой оптимизацией становится вообще ненужным ограничивать вручную число фаз алгоритма числом — он сам остановится через нужное число фаз.

void solve() {

vector<int> d (n, INF); d[v] = 0;

for (;;) {

bool any = false;

for (int j=0; j<m; ++j)

if (d[e[j].a] < INF)

if (d[e[j].b] > d[e[j].a] + e[j].cost) {

d[e[j].b] = d[e[j].a] + e[j].cost; any = true;

}

if (!any) break;

}

// вывод d, например, на экран

}

Восстановление путей

Рассмотрим теперь, как можно модифицировать алгоритм Форда-Беллмана так, чтобы он не только находил длины кратчайших путей, но и позволял восстанавливать сами кратчайшие пути.

е. предпоследнюю вершину в кратчайшем пути, ведущем в неё. В самом деле, кратчайший путь до какой-то вершины

является кратчайшим путём до какой-то вершины 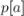, к которому приписали в конец вершину .

Заметим, что алгоритм Форда-Беллмана работает по такой же логике: он, предполагая, что кратчайшее расстояние до одной вершины уже посчитано, пытается улучшить кратчайшее расстояние до другой вершины. Следовательно, в момент улучшения нам надо просто запоминать в , из какой вершины это улучшение произошло.

Приведём реализацию Форда-Беллмана с восстановлением пути до какой-то заданной вершины :

void solve() {

vector<int> d (n, INF); d[v] = 0;

vector<int> p (n, -1);

for (;;) {

bool any = false;

for (int j=0; j<m; ++j)

if (d[e[j].a] < INF)

if (d[e[j].b] > d[e[j].a] + e[j].cost) { d[e[j].b] = d[e[j].a] + e[j].cost;

p[e[j].b] = e[j].a; any = true;

}

if (!any) break;

}

if (d[t] == INF)

cout << "No path from " << v << " to " << t << ".";

else {

vector<int> path;

for (int cur=t; cur!=-1; cur=p[cur]) path.push_back (cur);

reverse (path.begin(), path.end());

cout << "Path from " << v << " to " << t << ": "; for (size_t i=0; i<path.size(); ++i)

cout << path[i] << ' ';

}

}

Доказательство алгоритма

Иными словами, для любой вершины обозначим через число рёбер в кратчайшем пути до неё (если таких путей несколько, можно взять любой). Тогда это утверждение говорит о том, что после фаз этот кратчайший путь будет найден гарантированно.

Доказательство. Рассмотрим произвольную вершину , до которой существует путь из стартовой вершины ,

Форда-Беллмана, следовательно, расстояние до вершины было корректно посчитано после первой фазы. Повторяя эти утверждения раз, получаем, что после -й фазы расстояние до вершины посчитано корректно, что и требовалось доказать.

Последнее, что надо заметить — это то, что любой кратчайший путь не может иметь более ребра. Следовательно, алгоритму достаточно произвести только фазу. После этого ни одна релаксация гарантированно не может завершиться улучшением расстояния до какой-то вершины.

Случай отрицательного цикла

Выше мы везде считали, что отрицательного цикла в графе нет (уточним, нас интересует отрицательный цикл, достижимый из стартовой вершины , а недостижимые циклы ничего в вышеописанном алгоритме не меняют).

При его наличии возникают дополнительные сложности, связанные с тем, что расстояния до всех вершин на этом цикле, а также расстояния до достижимых из этого цикла вершин не определены — они должны быть равны минус бесконечности.

Нетрудно понять, что алгоритм Форда-Беллмана сможет бесконечно делать релаксации среди всех вершин этого цикла и вершин, достижимых из него. Следовательно, если не ограничивать число фаз числом , то алгоритм будет работать бесконечно, постоянно улучшая расстояния до этих вершин.

Отсюда мы получаем критерий наличия достижимого цикла отрицательного веса: если после фазы мы выполним ещё одну фазу, и на ней произойдёт хотя бы одна релаксация, то граф содержит цикл отрицательного веса, достижимый из ; в противном случае, такого цикла нет.

Более того, если такой цикл обнаружился, то алгоритм Форда-Беллмана можно модифицировать таким образом, чтобы он выводил сам этот цикл в виде последовательности вершин, входящих в него. Для этого достаточно запомнить номер вершины , в которой произошла релаксация на -ой фазе. Эта вершина будет либо лежать на цикле отрицательного веса, либо она достижима из него. Чтобы получить вершину, которая гарантированно лежит

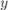на цикле, достаточно, например, раз пройти по предкам, начиная от вершины . Получив номер вершины, лежащей на цикле, надо пройтись от этой вершины по предкам, пока мы не вернёмся в эту же вершину (а это обязательно произойдёт, потому что релаксации в цикле отрицательного веса происходят по кругу).

Реализация:

void solve() {

vector<int> d (n, INF); d[v] = 0;

vector<int> p (n, -1); int x;

for (int i=0; i<n; ++i) {

x = -1;

for (int j=0; j<m; ++j)

if (d[e[j].a] < INF)

if (d[e[j].b] > d[e[j].a] + e[j].cost) { d[e[j].b] = max (-INF, d[e[j].a] + e

[j].cost);

p[e[j].b] = e[j].a; x = e[j].b;

}

}

if (x == -1)

cout << "No negative cycle from " << v;

else {

int y = x;

for (int i=0; i<n; ++i) y = p[y];

vector<int> path;

for (int cur=y; ; cur=p[cur]) { path.push_back (cur);

if (cur == y && path.size() > 1) break;

}

reverse (path.begin(), path.end());

cout << "Negative cycle: ";

for (size_t i=0; i<path.size(); ++i) cout << path[i] << ' ';

}

}

Поскольку при наличии отрицательного цикла за итераций алгоритма расстояния могли уйти далеко в минус (по всей видимости, до отрицательных чисел порядка ), в коде приняты дополнительные меры против такого целочисленного переполнения:

d[e[j].b] = max (-INF, d[e[j].a] + e[j].cost);

В приведённой выше реализации ищется отрицательный цикл, достижимый из некоторой стартовой вершины ; однако алгоритм можно модифицировать, чтобы он искал просто любой отрицательный цикл в графе. Для этого надо положить все расстояния равными нулю, а не бесконечности — так, как будто бы мы

ищем кратчайший путь изо всех вершин одновременно; на корректность обнаружения отрицательного цикла это не повлияет.

Дополнительно на тему этой задачи — см. отдельную статью "Поиск отрицательного цикла в графе".

Задачи в online judges

Список задач, которые можно решить с помощью алгоритма Форда-Беллмана:

● E-OLIMP #1453 "Форд-Беллман" [сложность: низкая]

● UVA #423 "MPI Maelstrom" [сложность: низкая] ● UVA #534 "Frogger" [сложность: средняя]

● UVA #10099 "The Tourist Guide" [сложность: средняя]

● UVA #515 "King" [сложность: средняя]

См. также список задач в статье "Поиск отрицательного цикла".