e-maxx_algo

e-maxx :: algo

Вас приветствует книга, собранная по материалам сайта e-maxx.ru/algo (по состоянию на 26 Apr 2012 1:48).

В этой книге Вы найдёте описание, реализации и доказательства множества алгоритмов, от известных всем до

тех, которые являются уделом лучших олимпиадников и специалистов по Computer Science. В конце приведены ссылки на тематическую литературу, которую можно скачать с моего сайта, а также немного информации обо мне.

Приятного чтения!

●Алгоритм Эдмондса нахождения наибольшего паросочетания в произвольных графах за O (N3)

●Покрытие путями ориентированного ациклического графа

●Матрица Татта. Рандомизированный алгоритм для поиска максимального паросочетания в произвольном графе

связность

●Рёберная связность. Свойства и нахождение

●Вершинная связность. Свойства и нахождение

●Построение графа с указанными величинами вершинной и рёберной связностей и наименьшей из степеней вершин

К-ые пути обратные задачи

●Обратная задача SSSP (inverse-SSSP - обратная задача кратчайших путей из одной вершины) за O (M)

●Обратная задача MST (inverse-MST - обратная задача минимального остова) за O (N M2)

разное

●Покраска рёбер дерева (структуры данных) - решение за O (log N)

●Задача 2-SAT (2-CNF). Решение за O (N + M)

●Heavy-light декомпозиция

Геометрия

элементарные алгоритмы

●Длина объединения отрезков на прямой за O (N log N)

●Знаковая площадь треугольника и предикат 'По часовой стрелке'

●Проверка двух отрезков на пересечение

●Нахождение уравнения прямой для отрезка

●Нахождение точки пересечения двух прямых

●Нахождение точки пересечения двух отрезков

●Нахождение площади простого многоугольника за O (N)

●Теорема Пика. Нахождение площади решётчатого многоугольника за O (1)

●Задача о покрытии отрезков точками

●Центры тяжести многоугольников и многогранников

более сложные алгоритмы

●Пересечение окружности и прямой

●Пересечение двух окружностей

●Построение выпуклой оболочки алгоритмом Грэхэма-Эндрю за O (N log N)

●Нахождение площади объединения треугольников. Метод вертикальной декомпозиции

●Проверка точки на принадлежность выпуклому многоугольнику за O (log N)

●Нахождение вписанной окружности в выпуклом многоугольнике с помощью тернарного поиска за O (N log2 C)

●Нахождение вписанной окружности в выпуклом многоугольнике методом сжатия сторон за O (N log N)

●Диаграмма Вороного в двумерном случае, её свойства, применение. Простейший алгоритм построения за O(N4)

●Нахождение всех граней, внешней грани планарного графа за O (N log N)

●Нахождение пары ближайших точек алгоритмом разделяй-и-властвуй за O (N log N)

●Преобразование геометрической инверсии

●Поиск общих касательных к двум окружностям

●Поиск пары пересекающихся отрезков алгоритмом заметающей прямой за O (N log N)

●Нахождение ранга матрицы за O (N3)

●Вычисление определителя матрицы методом Гаусса за O (N3)

●Вычисление определителя методом Краута за O (N3)

Численные методы

●Интегрирование по формуле Симпсона

●Поиск корней методом Ньютона (касательных)

●Тернарный поиск

Комбинаторика

●Биномиальные коэффициенты

●Числа Каталана

●Ожерелья

●Расстановка слонов на шахматной доске

●Правильные скобочные последовательности. Нахождение лексикографически следующей, K-ой, определение номера

●Количество помеченных графов, связных помеченных графов, помеченных графов с K компонентами связности

●Генерация сочетаний из N элементов

●Лемма Бернсайда. Теорема Пойа

●Принцип включений-исключений

Теория игр

●Игры на произвольных графах. Метод ретроспективного анализа за O (M)

●Теория Шпрага-Гранди. Ним

Расписания

●Задача Джонсона с одним станком

●Задача Джонсона с двумя станками

●Оптимальный выбор заданий при известных временах завершения и длительностях выполнения

Разное

●Задача Иосифа

●Игра Пятнашки: существование решения

●Дерево Штерна-Броко. Ряд Фарея

●Поиск подотрезка массива с максимальной/минимальной суммой за O(N)

Приложение

●Литература

●Об авторе

Функция Эйлера

Определение

Несколько первых значений этой функции (A000010 в энциклопедии OEIS):

Свойства

Три следующих простых свойства функции Эйлера — достаточны, чтобы научиться вычислять её для любых чисел:

●Если — простое число, то .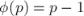

(Это очевидно, т.к. любое число, кроме самого 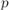, взаимно просто с ним.)

●Если 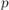— простое, — натуральное число, то .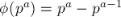

(Поскольку с числом 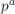не взаимно просты только числа вида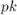 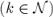, которых 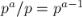штук.)

●Если и взаимно простые, то 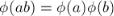("мультипликативность" функции Эйлера).

взаимно однозначно соответствует число 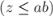, что и завершает доказательство.)

Отсюда можно получить функцию Эйлера для любого через его факторизацию (разложение на простые сомножители):

если

(где все 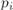— простые), то

Реализация

Простейший код, вычисляющий функцию Эйлера, факторизуя число элементарным методом за :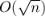

int phi (int n) {

int result = n;

for (int i=2; i*i<=n; ++i) if (n % i == 0) {

while (n % i == 0) n /= i;

result -= result / i;

}

if (n > 1)

result -= result / n; return result;

}

Ключевое место для вычисление функции Эйлера — это нахождение факторизации числа . Его можно осуществить за время, значительно меньшее : см. Эффективные алгоритмы факторизации.

Приложения функции Эйлера

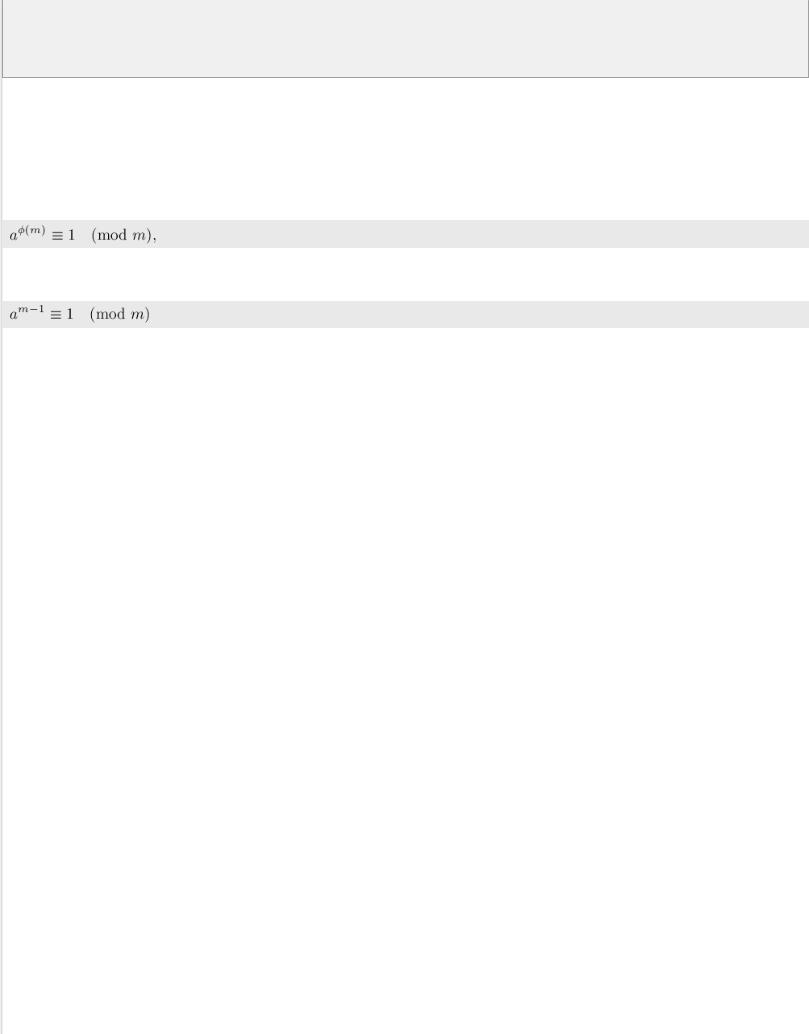
Самое известное и важное свойство функции Эйлера выражается в теореме Эйлера:

где и взаимно просты.

В частном случае, когда простое, теорема Эйлера превращается в так называемую малую теорему Ферма:

Теорема Эйлера достаточно часто встречается в практических приложениях, например, см. Обратный элемент в поле по модулю.

Задачи в online judges

Список задач, в которых требуется посчитать функцию Эйлера,либо воспользоваться теоремой Эйлера, либо по значению функции Эйлера восстанавливать исходное число:

● UVA #10179 "Irreducible Basic Fractions" [сложность: низкая]

● UVA #10299 "Relatives" [сложность: низкая]

● UVA #11327 "Enumerating Rational Numbers" [сложность: средняя]

● TIMUS #1673 "Допуск к экзамену" [сложность: высокая]

Бинарное возведение в степень

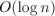Бинарное (двоичное) возведение в степень — это приём, позволяющий возводить любое число в -ую степень за умножений (вместо умножений при обычном подходе).

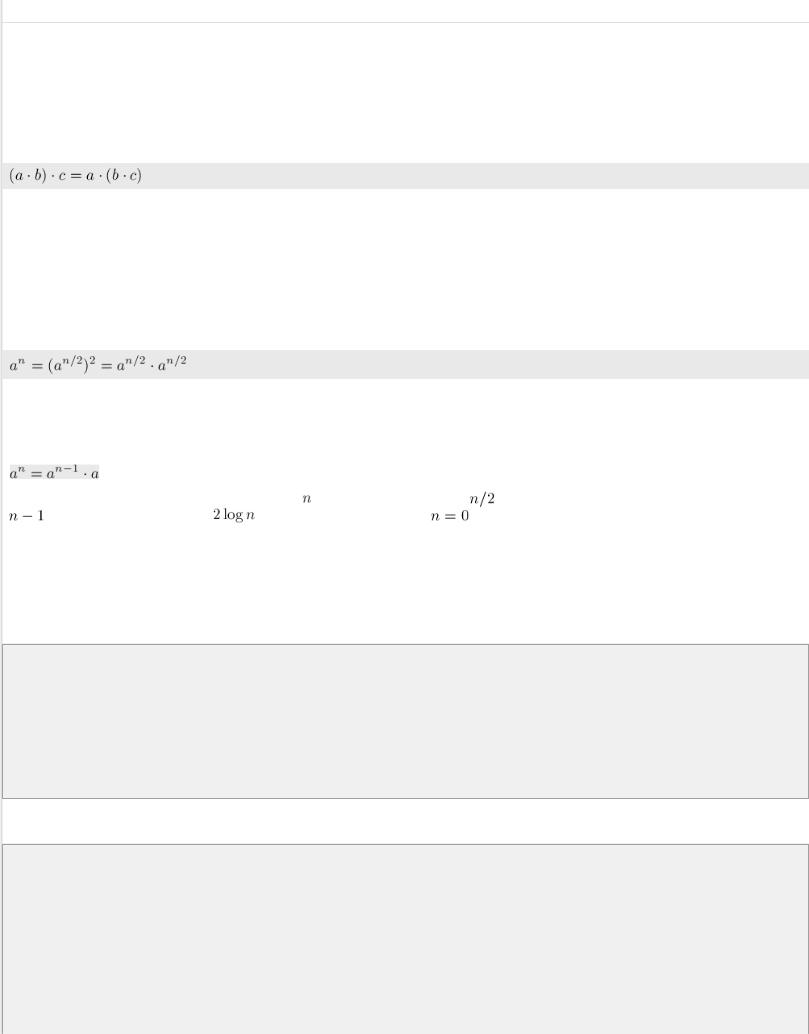
Более того, описываемый здесь приём применим к любой ассоциативной операции, а не только к умножению чисел. Напомним, операция называется ассоциативной, если для любых 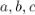выполняется:

Наиболее очевидное обобщение — на остатки по некоторому модулю (очевидно, ассоциативность сохраняется). Следующим по "популярности" является обобщение на произведение матриц (его ассоциативность общеизвестна).

Алгоритм

Заметим, что для любого числа и чётного числа выполнимо очевидное тождество (следующее из ассоциативности операции умножения):

Оно и является основным в методе бинарного возведения в степень. Действительно, для чётного мы показали, как, потратив всего одну операцию умножения, можно свести задачу к вдвое меньшей степени.

Осталось понять, что делать, если степень нечётна. Здесь мы поступаем очень просто: перейдём к степени 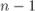, которая будет уже чётной:

рекуррентной формулы). Таким образом, мы получили алгоритм, работающий за 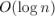умножений.

Реализация

Простейшая рекурсивная реализация:

int binpow (int a, int n) { if (n == 0)

return 1; if (n % 2 == 1)

return binpow (a, n-1) * a;

else {

int b = binpow (a, n/2); return b * b;

}

}

Нерекурсивная реализация, оптимизированная (деления на 2 заменены битовыми операциями):

int binpow (int a, int n) { int res = 1;

while (n)

if (n & 1) {

res *= a; --n;

}

else {

a *= a; n >>= 1;

}

return res;